Learning and Transferring Sparse Contextual Bigrams with Linear Transformers

Transformers have excelled in natural language modeling and one reason behind this success is their exceptional ability to combine contextual informal and global knowledge. However, the theoretical basis remains unclear. In this paper, first we introduce the Sparse Contextual Bigram (SCB), a natural extension of the classical bigram model, where the next token's generation depends on a sparse set of earlier positions determined by the last token. We then analyze the training dynamics and sample complexity of learning SCB using a one-layer linear transformer with a gradient-based algorithm. We show that when trained from scratch, the training process can be split into an initial sample-intensive stage where the correlation is boosted from zero to a nontrivial value, followed by a more sample-efficient stage of further improvement. Additionally, we prove that, provided a nontrivial correlation between the downstream and pretraining tasks, finetuning from a pretrained model allows us to bypass the initial sample-intensive stage. We also empirically demonstrate that our algorithm can outperform SGD in this setting and discuss its relationship with the usual softmax-based transformers.

Learning Orthogonal Multi-Index Models: A Fine-Grained Information Exponent Analysis

The information exponent (Ben Arous et al. [2021]) -- which is equivalent to the lowest degree in the Hermite expansion of the link function for Gaussian single-index models -- has played an important role in predicting the sample complexity of online stochastic gradient descent (SGD) in various learning tasks. In this work, we demonstrate that, for multi-index models, focusing solely on the lowest degree can miss key structural details of the model and result in suboptimal rates. Specifically, we consider the task of learning target functions of form $f_*(\mathbf{x}) = \sum_{k=1}^{P} \phi(\mathbf{v}_k^* \cdot \mathbf{x})$, where $P \ll d$, the ground-truth directions $\{ \mathbf{v}_k^* \}_{k=1}^P$ are orthonormal, and only the second and $2L$-th Hermite coefficients of the link function $\phi$ can be nonzero. Based on the theory of information exponent, when the lowest degree is $2L$, recovering the directions requires $d^{2L-1}\mathrm{poly}(P)$ samples, and when the lowest degree is $2$, only the relevant subspace (not the exact directions) can be recovered due to the rotational invariance of the second-order terms. In contrast, we show that by considering both second- and higher-order terms, we can first learn the relevant space via the second-order terms, and then the exact directions using the higher-order terms, and the overall sample and complexity of online SGD is $d \mathrm{poly}(P)$.

On the Importance of Contrastive Loss in Multimodal Learning

Recently, contrastive learning approaches (e.g., CLIP (Radford et al., 2021)) have received huge success in multimodal learning, where the model tries to minimize the distance between the representations of different views (e.g., image and its caption) of the same data point while keeping the representations of different data points away from each other. However, from a theoretical perspective, it is unclear how contrastive learning can learn the representations from different views efficiently, especially when the data is not isotropic. In this work, we analyze the training dynamics of a simple multimodal contrastive learning model and show that contrastive pairs are important for the model to efficiently balance the learned representations. In particular, we show that the positive pairs will drive the model to align the representations at the cost of increasing the condition number, while the negative pairs will reduce the condition number, keeping the learned representations balanced.

Depth Separation with Multilayer Mean-Field Networks

Depth separation -- why a deeper network is more powerful than a shallower one -- has been a major problem in deep learning theory. Previous results often focus on representation power. For example, arXiv:1904.06984 constructed a function that is easy to approximate using a 3-layer network but not approximable by any 2-layer network. In this paper, we show that this separation is in fact algorithmic: one can learn the function constructed by arXiv:1904.06984 using an overparameterized network with polynomially many neurons efficiently. Our result relies on a new way of extending the mean-field limit to multilayer networks, and a decomposition of loss that factors out the error introduced by the discretization of infinite-width mean-field networks.

Understanding Deflation Process in Over-parametrized Tensor Decomposition

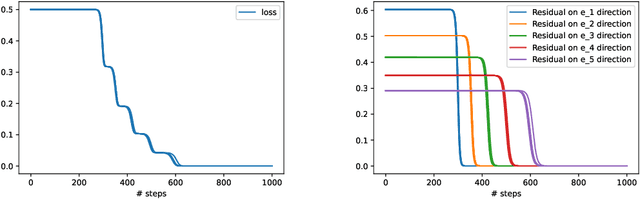
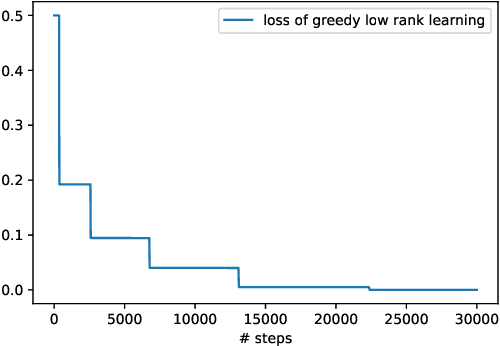
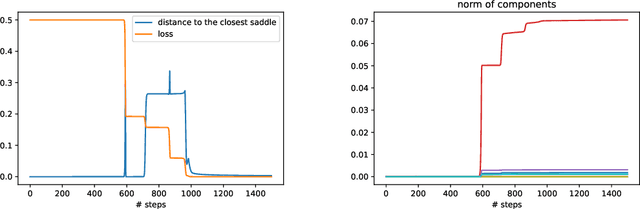
In this paper we study the training dynamics for gradient flow on over-parametrized tensor decomposition problems. Empirically, such training process often first fits larger components and then discovers smaller components, which is similar to a tensor deflation process that is commonly used in tensor decomposition algorithms. We prove that for orthogonally decomposable tensor, a slightly modified version of gradient flow would follow a tensor deflation process and recover all the tensor components. Our proof suggests that for orthogonal tensors, gradient flow dynamics works similarly as greedy low-rank learning in the matrix setting, which is a first step towards understanding the implicit regularization effect of over-parametrized models for low-rank tensors.