Models That Are Interpretable But Not Transparent

Faithful explanations are essential for machine learning models in high-stakes applications. Inherently interpretable models are well-suited for these applications because they naturally provide faithful explanations by revealing their decision logic. However, model designers often need to keep these models proprietary to maintain their value. This creates a tension: we need models that are interpretable--allowing human decision-makers to understand and justify predictions, but not transparent, so that the model's decision boundary is not easily replicated by attackers. Shielding the model's decision boundary is particularly challenging alongside the requirement of completely faithful explanations, since such explanations reveal the true logic of the model for an entire subspace around each query point. This work provides an approach, FaithfulDefense, that creates model explanations for logical models that are completely faithful, yet reveal as little as possible about the decision boundary. FaithfulDefense is based on a maximum set cover formulation, and we provide multiple formulations for it, taking advantage of submodularity.

Amazing Things Come From Having Many Good Models

The Rashomon Effect, coined by Leo Breiman, describes the phenomenon that there exist many equally good predictive models for the same dataset. This phenomenon happens for many real datasets and when it does, it sparks both magic and consternation, but mostly magic. In light of the Rashomon Effect, this perspective piece proposes reshaping the way we think about machine learning, particularly for tabular data problems in the nondeterministic (noisy) setting. We address how the Rashomon Effect impacts (1) the existence of simple-yet-accurate models, (2) flexibility to address user preferences, such as fairness and monotonicity, without losing performance, (3) uncertainty in predictions, fairness, and explanations, (4) reliable variable importance, (5) algorithm choice, specifically, providing advanced knowledge of which algorithms might be suitable for a given problem, and (6) public policy. We also discuss a theory of when the Rashomon Effect occurs and why. Our goal is to illustrate how the Rashomon Effect can have a massive impact on the use of machine learning for complex problems in society.

OKRidge: Scalable Optimal k-Sparse Ridge Regression for Learning Dynamical Systems

We consider an important problem in scientific discovery, identifying sparse governing equations for nonlinear dynamical systems. This involves solving sparse ridge regression problems to provable optimality in order to determine which terms drive the underlying dynamics. We propose a fast algorithm, OKRidge, for sparse ridge regression, using a novel lower bound calculation involving, first, a saddle point formulation, and from there, either solving (i) a linear system or (ii) using an ADMM-based approach, where the proximal operators can be efficiently evaluated by solving another linear system and an isotonic regression problem. We also propose a method to warm-start our solver, which leverages a beam search. Experimentally, our methods attain provable optimality with run times that are orders of magnitude faster than those of the existing MIP formulations solved by the commercial solver Gurobi.

Understanding and Exploring the Whole Set of Good Sparse Generalized Additive Models

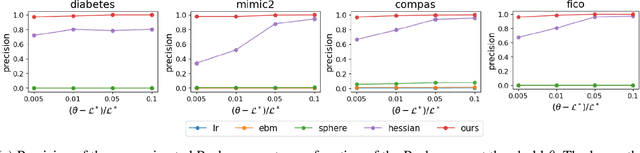
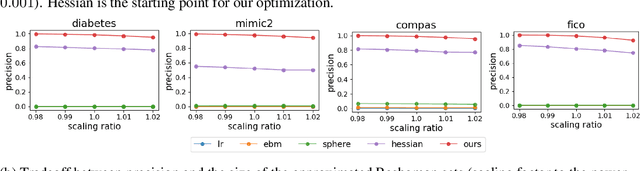
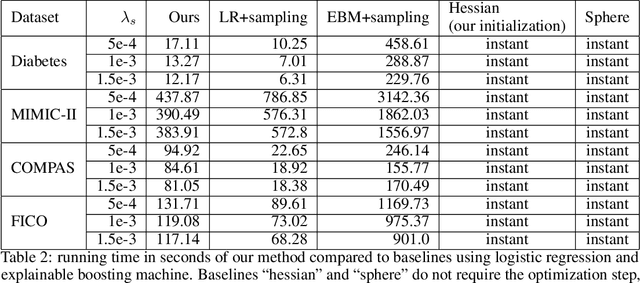
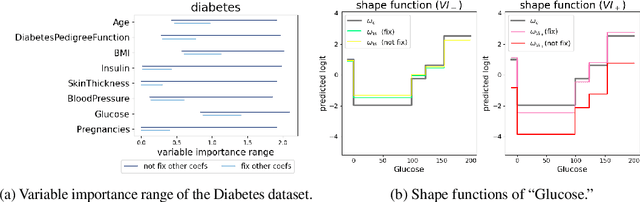
In real applications, interaction between machine learning model and domain experts is critical; however, the classical machine learning paradigm that usually produces only a single model does not facilitate such interaction. Approximating and exploring the Rashomon set, i.e., the set of all near-optimal models, addresses this practical challenge by providing the user with a searchable space containing a diverse set of models from which domain experts can choose. We present a technique to efficiently and accurately approximate the Rashomon set of sparse, generalized additive models (GAMs). We present algorithms to approximate the Rashomon set of GAMs with ellipsoids for fixed support sets and use these ellipsoids to approximate Rashomon sets for many different support sets. The approximated Rashomon set serves as a cornerstone to solve practical challenges such as (1) studying the variable importance for the model class; (2) finding models under user-specified constraints (monotonicity, direct editing); (3) investigating sudden changes in the shape functions. Experiments demonstrate the fidelity of the approximated Rashomon set and its effectiveness in solving practical challenges.

FasterRisk: Fast and Accurate Interpretable Risk Scores

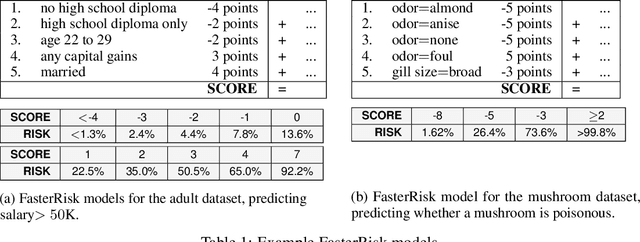
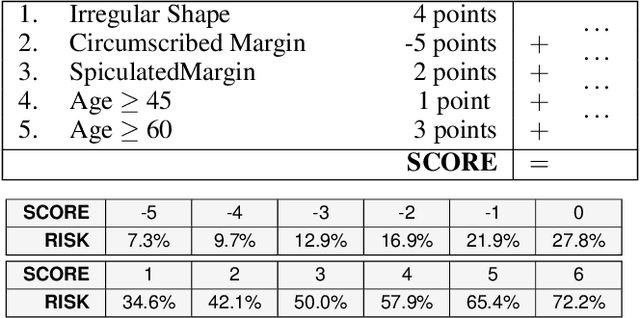
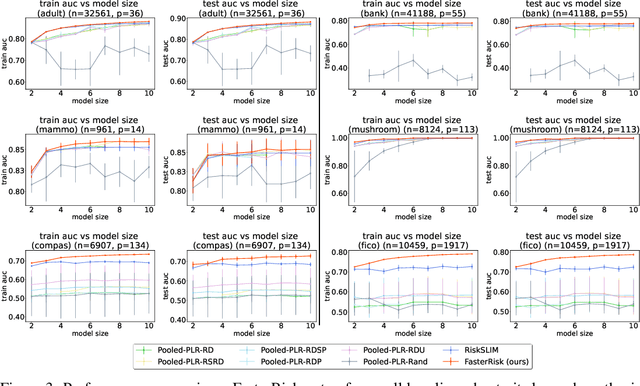
Over the last century, risk scores have been the most popular form of predictive model used in healthcare and criminal justice. Risk scores are sparse linear models with integer coefficients; often these models can be memorized or placed on an index card. Typically, risk scores have been created either without data or by rounding logistic regression coefficients, but these methods do not reliably produce high-quality risk scores. Recent work used mathematical programming, which is computationally slow. We introduce an approach for efficiently producing a collection of high-quality risk scores learned from data. Specifically, our approach produces a pool of almost-optimal sparse continuous solutions, each with a different support set, using a beam-search algorithm. Each of these continuous solutions is transformed into a separate risk score through a "star ray" search, where a range of multipliers are considered before rounding the coefficients sequentially to maintain low logistic loss. Our algorithm returns all of these high-quality risk scores for the user to consider. This method completes within minutes and can be valuable in a broad variety of applications.

TimberTrek: Exploring and Curating Sparse Decision Trees with Interactive Visualization

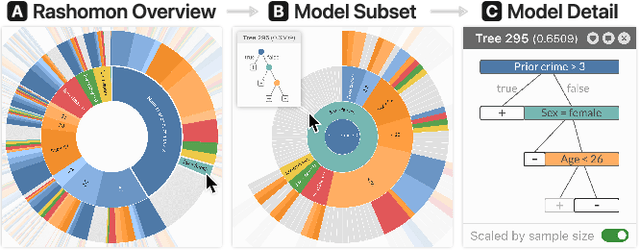
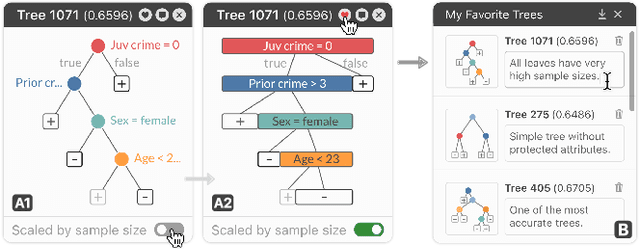
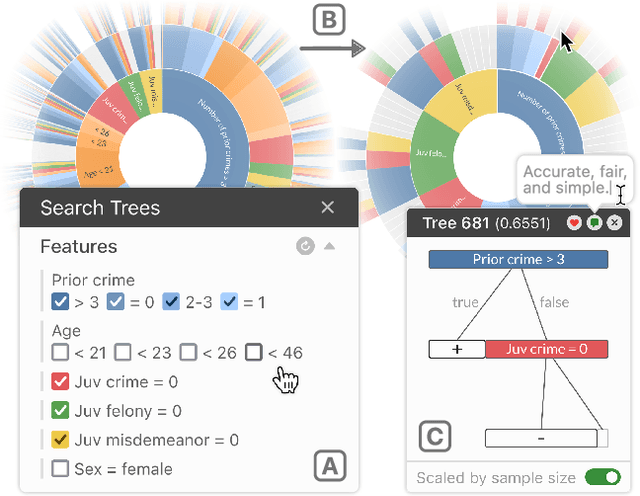
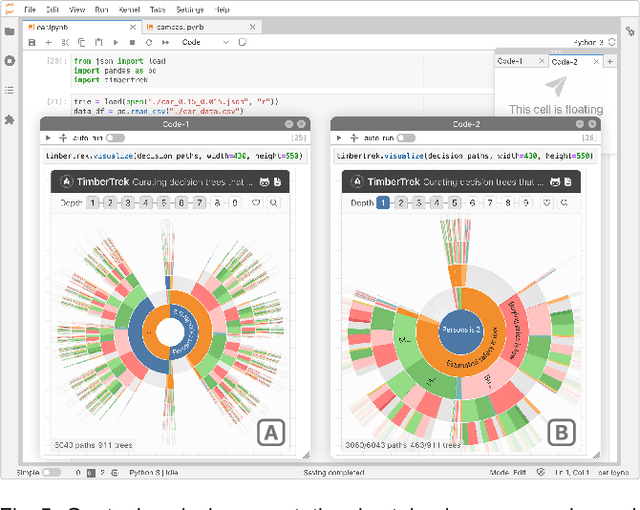
Given thousands of equally accurate machine learning (ML) models, how can users choose among them? A recent ML technique enables domain experts and data scientists to generate a complete Rashomon set for sparse decision trees--a huge set of almost-optimal interpretable ML models. To help ML practitioners identify models with desirable properties from this Rashomon set, we develop TimberTrek, the first interactive visualization system that summarizes thousands of sparse decision trees at scale. Two usage scenarios highlight how TimberTrek can empower users to easily explore, compare, and curate models that align with their domain knowledge and values. Our open-source tool runs directly in users' computational notebooks and web browsers, lowering the barrier to creating more responsible ML models. TimberTrek is available at the following public demo link: https://poloclub.github.io/timbertrek.

Exploring the Whole Rashomon Set of Sparse Decision Trees

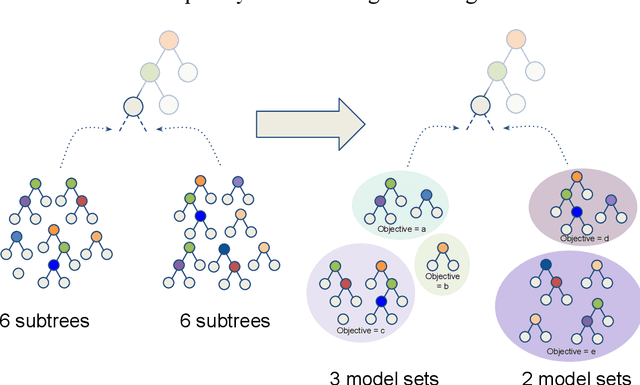
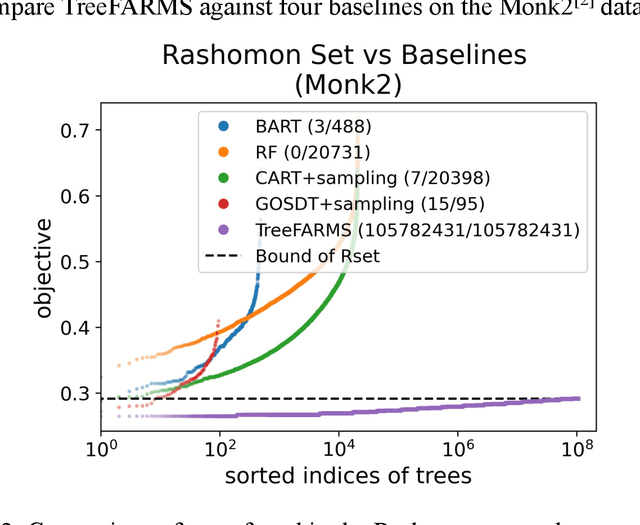
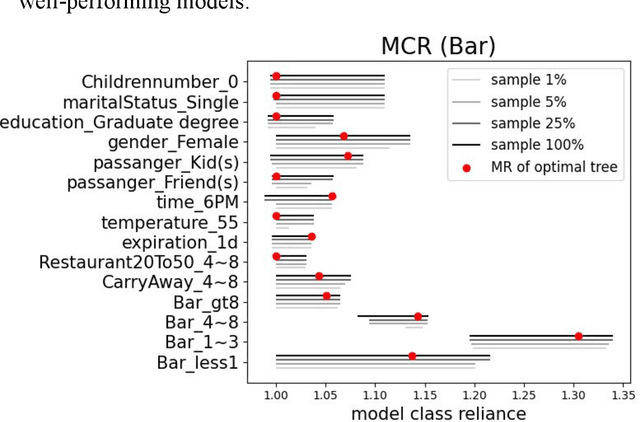
In any given machine learning problem, there may be many models that could explain the data almost equally well. However, most learning algorithms return only one of these models, leaving practitioners with no practical way to explore alternative models that might have desirable properties beyond what could be expressed within a loss function. The Rashomon set is the set of these all almost-optimal models. Rashomon sets can be extremely complicated, particularly for highly nonlinear function classes that allow complex interaction terms, such as decision trees. We provide the first technique for completely enumerating the Rashomon set for sparse decision trees; in fact, our work provides the first complete enumeration of any Rashomon set for a non-trivial problem with a highly nonlinear discrete function class. This allows the user an unprecedented level of control over model choice among all models that are approximately equally good. We represent the Rashomon set in a specialized data structure that supports efficient querying and sampling. We show three applications of the Rashomon set: 1) it can be used to study variable importance for the set of almost-optimal trees (as opposed to a single tree), 2) the Rashomon set for accuracy enables enumeration of the Rashomon sets for balanced accuracy and F1-score, and 3) the Rashomon set for a full dataset can be used to produce Rashomon sets constructed with only subsets of the data set. Thus, we are able to examine Rashomon sets across problems with a new lens, enabling users to choose models rather than be at the mercy of an algorithm that produces only a single model.

Fast Sparse Classification for Generalized Linear and Additive Models

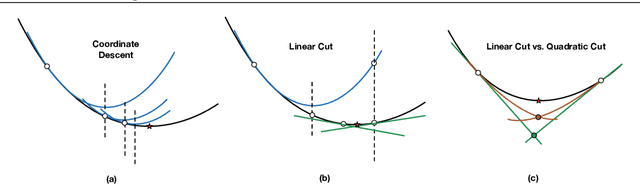
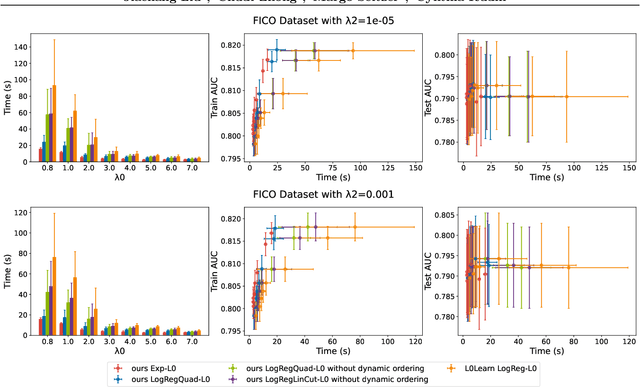
We present fast classification techniques for sparse generalized linear and additive models. These techniques can handle thousands of features and thousands of observations in minutes, even in the presence of many highly correlated features. For fast sparse logistic regression, our computational speed-up over other best-subset search techniques owes to linear and quadratic surrogate cuts for the logistic loss that allow us to efficiently screen features for elimination, as well as use of a priority queue that favors a more uniform exploration of features. As an alternative to the logistic loss, we propose the exponential loss, which permits an analytical solution to the line search at each iteration. Our algorithms are generally 2 to 5 times faster than previous approaches. They produce interpretable models that have accuracy comparable to black box models on challenging datasets.

Fast Sparse Decision Tree Optimization via Reference Ensembles

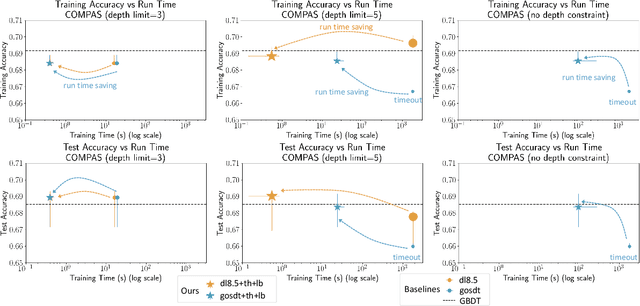
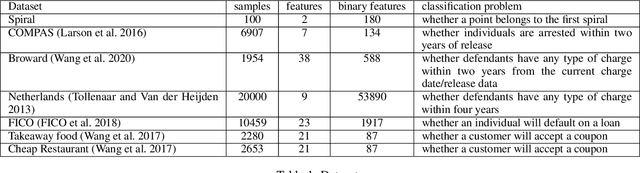
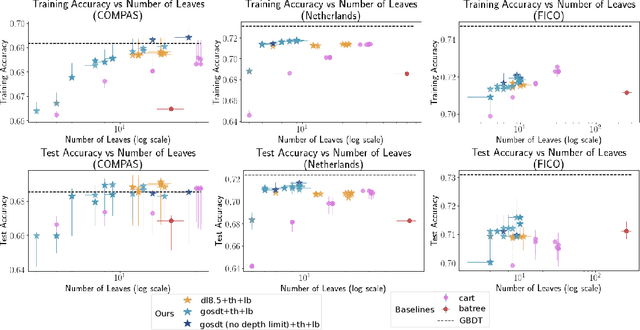
Sparse decision tree optimization has been one of the most fundamental problems in AI since its inception and is a challenge at the core of interpretable machine learning. Sparse decision tree optimization is computationally hard, and despite steady effort since the 1960's, breakthroughs have only been made on the problem within the past few years, primarily on the problem of finding optimal sparse decision trees. However, current state-of-the-art algorithms often require impractical amounts of computation time and memory to find optimal or near-optimal trees for some real-world datasets, particularly those having several continuous-valued features. Given that the search spaces of these decision tree optimization problems are massive, can we practically hope to find a sparse decision tree that competes in accuracy with a black box machine learning model? We address this problem via smart guessing strategies that can be applied to any optimal branch-and-bound-based decision tree algorithm. We show that by using these guesses, we can reduce the run time by multiple orders of magnitude, while providing bounds on how far the resulting trees can deviate from the black box's accuracy and expressive power. Our approach enables guesses about how to bin continuous features, the size of the tree, and lower bounds on the error for the optimal decision tree. Our experiments show that in many cases we can rapidly construct sparse decision trees that match the accuracy of black box models. To summarize: when you are having trouble optimizing, just guess.

Interpretable Machine Learning: Fundamental Principles and 10 Grand Challenges

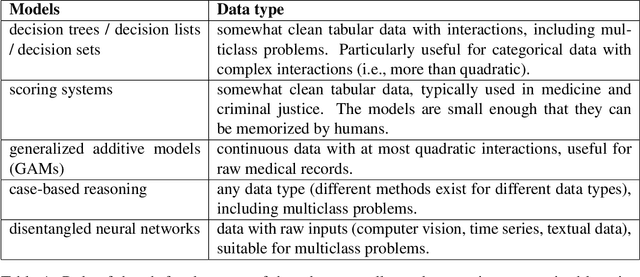
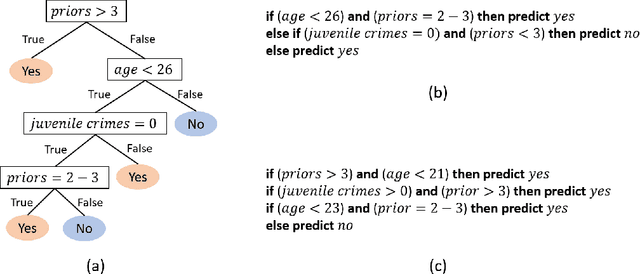
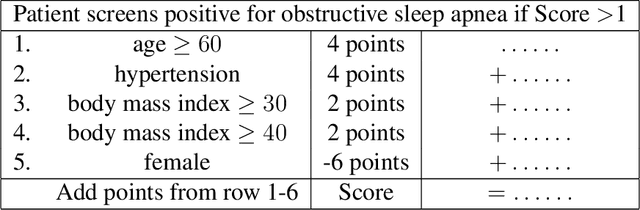
Interpretability in machine learning (ML) is crucial for high stakes decisions and troubleshooting. In this work, we provide fundamental principles for interpretable ML, and dispel common misunderstandings that dilute the importance of this crucial topic. We also identify 10 technical challenge areas in interpretable machine learning and provide history and background on each problem. Some of these problems are classically important, and some are recent problems that have arisen in the last few years. These problems are: (1) Optimizing sparse logical models such as decision trees; (2) Optimization of scoring systems; (3) Placing constraints into generalized additive models to encourage sparsity and better interpretability; (4) Modern case-based reasoning, including neural networks and matching for causal inference; (5) Complete supervised disentanglement of neural networks; (6) Complete or even partial unsupervised disentanglement of neural networks; (7) Dimensionality reduction for data visualization; (8) Machine learning models that can incorporate physics and other generative or causal constraints; (9) Characterization of the "Rashomon set" of good models; and (10) Interpretable reinforcement learning. This survey is suitable as a starting point for statisticians and computer scientists interested in working in interpretable machine learning.