Reconstruction Target Matters in Masked Image Modeling for Cross-Domain Few-Shot Learning

Cross-Domain Few-Shot Learning (CDFSL) requires the model to transfer knowledge from the data-abundant source domain to data-scarce target domains for fast adaptation, where the large domain gap makes CDFSL a challenging problem. Masked Autoencoder (MAE) excels in effectively using unlabeled data and learning image's global structures, enhancing model generalization and robustness. However, in the CDFSL task with significant domain shifts, we find MAE even shows lower performance than the baseline supervised models. In this paper, we first delve into this phenomenon for an interpretation. We find that MAE tends to focus on low-level domain information during reconstructing pixels while changing the reconstruction target to token features could mitigate this problem. However, not all features are beneficial, as we then find reconstructing high-level features can hardly improve the model's transferability, indicating a trade-off between filtering domain information and preserving the image's global structure. In all, the reconstruction target matters for the CDFSL task. Based on the above findings and interpretations, we further propose Domain-Agnostic Masked Image Modeling (DAMIM) for the CDFSL task. DAMIM includes an Aggregated Feature Reconstruction module to automatically aggregate features for reconstruction, with balanced learning of domain-agnostic information and images' global structure, and a Lightweight Decoder module to further benefit the encoder's generalizability. Experiments on four CDFSL datasets demonstrate that our method achieves state-of-the-art performance.

MD-inferred neural network monoclinic finite-strain hyperelasticity models for $β$-HMX: Sobolev training and validation against physical constraints

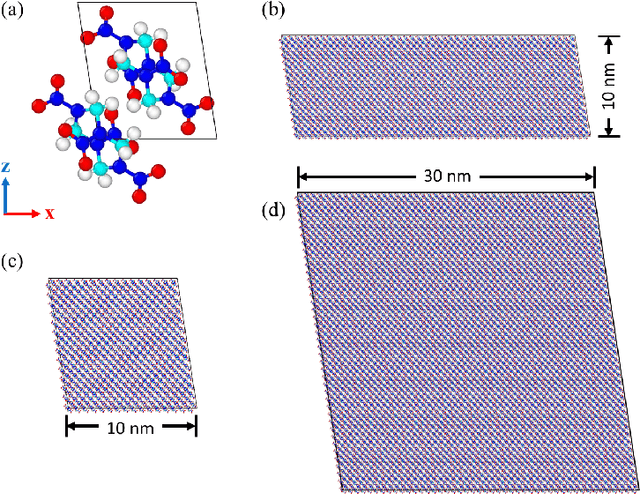
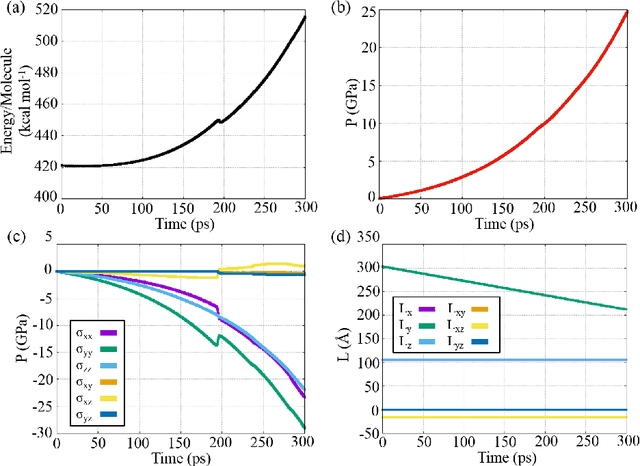
We present a machine learning framework to train and validate neural networks to predict the anisotropic elastic response of the monoclinic organic molecular crystal $\beta$-HMX in the geometrical nonlinear regime. A filtered molecular dynamic (MD) simulations database is used to train the neural networks with a Sobolev norm that uses the stress measure and a reference configuration to deduce the elastic stored energy functional. To improve the accuracy of the elasticity tangent predictions originating from the learned stored energy, a transfer learning technique is used to introduce additional tangential constraints from the data while necessary conditions (e.g. strong ellipticity, crystallographic symmetry) for the correctness of the model are either introduced as additional physical constraints or incorporated in the validation tests. Assessment of the neural networks is based on (1) the accuracy with which they reproduce the bottom-line constitutive responses predicted by MD, (2) detailed examination of their stability and uniqueness, and (3) admissibility of the predicted responses with respect to continuum mechanics theory in the finite-deformation regime. We compare the neural networks' training efficiency under different Sobolev constraints and assess the models' accuracy and robustness against MD benchmarks for $\beta$-HMX.

Equivariant geometric learning for digital rock physics: estimating formation factor and effective permeability tensors from Morse graph

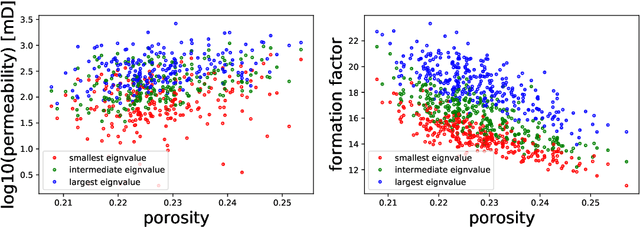
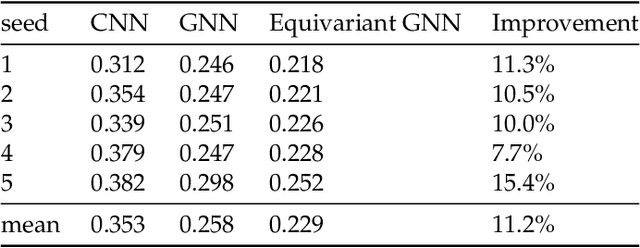
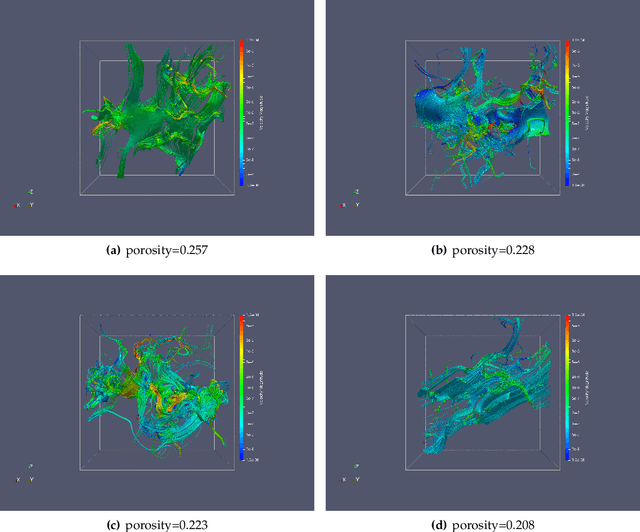
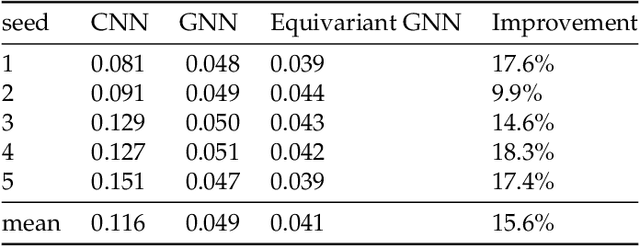
We present a SE(3)-equivariant graph neural network (GNN) approach that directly predicting the formation factor and effective permeability from micro-CT images. FFT solvers are established to compute both the formation factor and effective permeability, while the topology and geometry of the pore space are represented by a persistence-based Morse graph. Together, they constitute the database for training, validating, and testing the neural networks. While the graph and Euclidean convolutional approaches both employ neural networks to generate low-dimensional latent space to represent the features of the micro-structures for forward predictions, the SE(3) equivariant neural network is found to generate more accurate predictions, especially when the training data is limited. Numerical experiments have also shown that the new SE(3) approach leads to predictions that fulfill the material frame indifference whereas the predictions from classical convolutional neural networks (CNN) may suffer from spurious dependence on the coordinate system of the training data. Comparisons among predictions inferred from training the CNN and those from graph convolutional neural networks (GNN) with and without the equivariant constraint indicate that the equivariant graph neural network seems to perform better than the CNN and GNN without enforcing equivariant constraints.

Geometric deep learning for computational mechanics Part I: Anisotropic Hyperelasticity

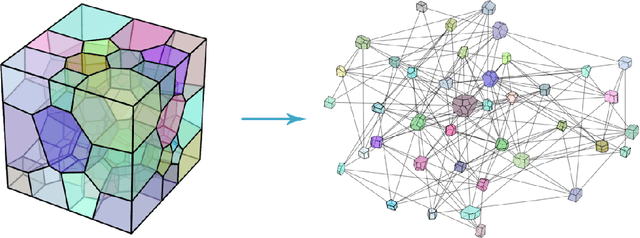
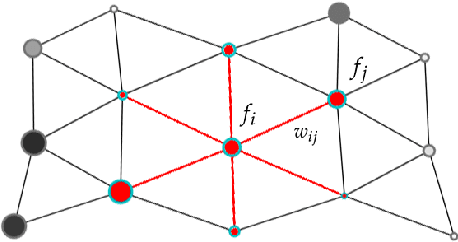
This paper is the first attempt to use geometric deep learning and Sobolev training to incorporate non-Euclidean microstructural data such that anisotropic hyperelastic material machine learning models can be trained in the finite deformation range. While traditional hyperelasticity models often incorporate homogenized measures of microstructural attributes, such as porosity averaged orientation of constitutes, these measures cannot reflect the topological structures of the attributes. We fill this knowledge gap by introducing the concept of weighted graph as a new mean to store topological information, such as the connectivity of anisotropic grains in assembles. Then, by leveraging a graph convolutional deep neural network architecture in the spectral domain, we introduce a mechanism to incorporate these non-Euclidean weighted graph data directly as input for training and for predicting the elastic responses of materials with complex microstructures. To ensure smoothness and prevent non-convexity of the trained stored energy functional, we introduce a Sobolev training technique for neural networks such that stress measure is obtained implicitly from taking directional derivatives of the trained energy functional. By optimizing the neural network to approximate both the energy functional output and the stress measure, we introduce a training procedure the improves efficiency and generalize the learned energy functional for different microstructures. The trained hybrid neural network model is then used to generate new stored energy functional for unseen microstructures in a parametric study to predict the influence of elastic anisotropy on the nucleation and propagation of fracture in the brittle regime.