A review on data-driven constitutive laws for solids

This review article highlights state-of-the-art data-driven techniques to discover, encode, surrogate, or emulate constitutive laws that describe the path-independent and path-dependent response of solids. Our objective is to provide an organized taxonomy to a large spectrum of methodologies developed in the past decades and to discuss the benefits and drawbacks of the various techniques for interpreting and forecasting mechanics behavior across different scales. Distinguishing between machine-learning-based and model-free methods, we further categorize approaches based on their interpretability and on their learning process/type of required data, while discussing the key problems of generalization and trustworthiness. We attempt to provide a road map of how these can be reconciled in a data-availability-aware context. We also touch upon relevant aspects such as data sampling techniques, design of experiments, verification, and validation.

Physics-Informed Diffusion Models

Generative models such as denoising diffusion models are quickly advancing their ability to approximate highly complex data distributions. They are also increasingly leveraged in scientific machine learning, where samples from the implied data distribution are expected to adhere to specific governing equations. We present a framework to inform denoising diffusion models on underlying constraints on such generated samples during model training. Our approach improves the alignment of the generated samples with the imposed constraints and significantly outperforms existing methods without affecting inference speed. Additionally, our findings suggest that incorporating such constraints during training provides a natural regularization against overfitting. Our framework is easy to implement and versatile in its applicability for imposing equality and inequality constraints as well as auxiliary optimization objectives.

Prediction of Effective Elastic Moduli of Rocks using Graph Neural Networks

This study presents a Graph Neural Networks (GNNs)-based approach for predicting the effective elastic moduli of rocks from their digital CT-scan images. We use the Mapper algorithm to transform 3D digital rock images into graph datasets, encapsulating essential geometrical information. These graphs, after training, prove effective in predicting elastic moduli. Our GNN model shows robust predictive capabilities across various graph sizes derived from various subcube dimensions. Not only does it perform well on the test dataset, but it also maintains high prediction accuracy for unseen rocks and unexplored subcube sizes. Comparative analysis with Convolutional Neural Networks (CNNs) reveals the superior performance of GNNs in predicting unseen rock properties. Moreover, the graph representation of microstructures significantly reduces GPU memory requirements (compared to the grid representation for CNNs), enabling greater flexibility in the batch size selection. This work demonstrates the potential of GNN models in enhancing the prediction accuracy of rock properties and boosting the efficiency of digital rock analysis.

Discovering interpretable elastoplasticity models via the neural polynomial method enabled symbolic regressions

Conventional neural network elastoplasticity models are often perceived as lacking interpretability. This paper introduces a two-step machine-learning approach that returns mathematical models interpretable by human experts. In particular, we introduce a surrogate model where yield surfaces are expressed in terms of a set of single-variable feature mappings obtained from supervised learning. A postprocessing step is then used to re-interpret the set of single-variable neural network mapping functions into mathematical form through symbolic regression. This divide-and-conquer approach provides several important advantages. First, it enables us to overcome the scaling issue of symbolic regression algorithms. From a practical perspective, it enhances the portability of learned models for partial differential equation solvers written in different programming languages. Finally, it enables us to have a concrete understanding of the attributes of the materials, such as convexity and symmetries of models, through automated derivations and reasoning. Numerical examples have been provided, along with an open-source code to enable third-party validation.

Synthesizing realistic sand assemblies with denoising diffusion in latent space

The shapes and morphological features of grains in sand assemblies have far-reaching implications in many engineering applications, such as geotechnical engineering, computer animations, petroleum engineering, and concentrated solar power. Yet, our understanding of the influence of grain geometries on macroscopic response is often only qualitative, due to the limited availability of high-quality 3D grain geometry data. In this paper, we introduce a denoising diffusion algorithm that uses a set of point clouds collected from the surface of individual sand grains to generate grains in the latent space. By employing a point cloud autoencoder, the three-dimensional point cloud structures of sand grains are first encoded into a lower-dimensional latent space. A generative denoising diffusion probabilistic model is trained to produce synthetic sand that maximizes the log-likelihood of the generated samples belonging to the original data distribution measured by a Kullback-Leibler divergence. Numerical experiments suggest that the proposed method is capable of generating realistic grains with morphology, shapes and sizes consistent with the training data inferred from an F50 sand database. We then use a rigid contact dynamic simulator to pour the synthetic sand in a confined volume to form granular assemblies in a static equilibrium state with targeted distribution properties. To ensure third-party validation, 50,000 synthetic sand grains and the 1,542 real synchrotron microcomputed tomography (SMT) scans of the F50 sand, as well as the granular assemblies composed of synthetic sand grains are made available in an open-source repository.

Denoising diffusion algorithm for inverse design of microstructures with fine-tuned nonlinear material properties

In this paper, we introduce a denoising diffusion algorithm to discover microstructures with nonlinear fine-tuned properties. Denoising diffusion probabilistic models are generative models that use diffusion-based dynamics to gradually denoise images and generate realistic synthetic samples. By learning the reverse of a Markov diffusion process, we design an artificial intelligence to efficiently manipulate the topology of microstructures to generate a massive number of prototypes that exhibit constitutive responses sufficiently close to designated nonlinear constitutive responses. To identify the subset of microstructures with sufficiently precise fine-tuned properties, a convolutional neural network surrogate is trained to replace high-fidelity finite element simulations to filter out prototypes outside the admissible range. The results of this study indicate that the denoising diffusion process is capable of creating microstructures of fine-tuned nonlinear material properties within the latent space of the training data. More importantly, the resulting algorithm can be easily extended to incorporate additional topological and geometric modifications by introducing high-dimensional structures embedded in the latent space. The algorithm is tested on the open-source mechanical MNIST data set. Consequently, this algorithm is not only capable of performing inverse design of nonlinear effective media but also learns the nonlinear structure-property map to quantitatively understand the multiscale interplay among the geometry and topology and their effective macroscopic properties.

Design of experiments for the calibration of history-dependent models via deep reinforcement learning and an enhanced Kalman filter

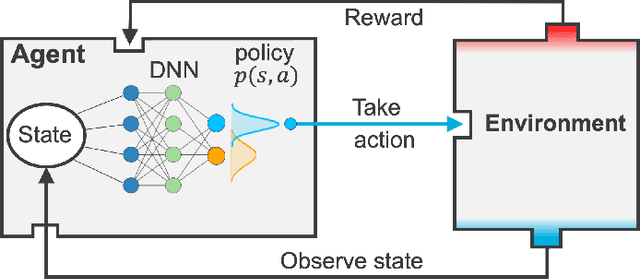
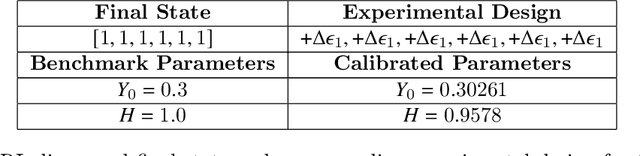
Experimental data is costly to obtain, which makes it difficult to calibrate complex models. For many models an experimental design that produces the best calibration given a limited experimental budget is not obvious. This paper introduces a deep reinforcement learning (RL) algorithm for design of experiments that maximizes the information gain measured by Kullback-Leibler (KL) divergence obtained via the Kalman filter (KF). This combination enables experimental design for rapid online experiments where traditional methods are too costly. We formulate possible configurations of experiments as a decision tree and a Markov decision process (MDP), where a finite choice of actions is available at each incremental step. Once an action is taken, a variety of measurements are used to update the state of the experiment. This new data leads to a Bayesian update of the parameters by the KF, which is used to enhance the state representation. In contrast to the Nash-Sutcliffe efficiency (NSE) index, which requires additional sampling to test hypotheses for forward predictions, the KF can lower the cost of experiments by directly estimating the values of new data acquired through additional actions. In this work our applications focus on mechanical testing of materials. Numerical experiments with complex, history-dependent models are used to verify the implementation and benchmark the performance of the RL-designed experiments.

Geometric deep learning for computational mechanics Part II: Graph embedding for interpretable multiscale plasticity

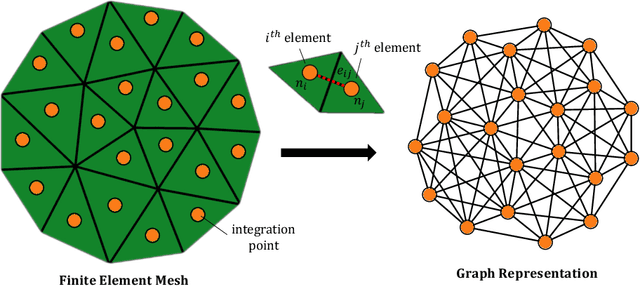
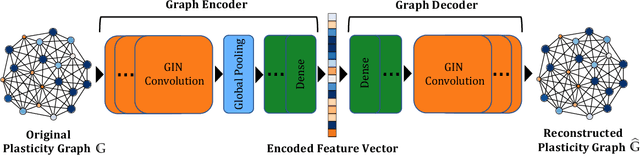
The history-dependent behaviors of classical plasticity models are often driven by internal variables evolved according to phenomenological laws. The difficulty to interpret how these internal variables represent a history of deformation, the lack of direct measurement of these internal variables for calibration and validation, and the weak physical underpinning of those phenomenological laws have long been criticized as barriers to creating realistic models. In this work, geometric machine learning on graph data (e.g. finite element solutions) is used as a means to establish a connection between nonlinear dimensional reduction techniques and plasticity models. Geometric learning-based encoding on graphs allows the embedding of rich time-history data onto a low-dimensional Euclidean space such that the evolution of plastic deformation can be predicted in the embedded feature space. A corresponding decoder can then convert these low-dimensional internal variables back into a weighted graph such that the dominating topological features of plastic deformation can be observed and analyzed.

Manifold embedding data-driven mechanics

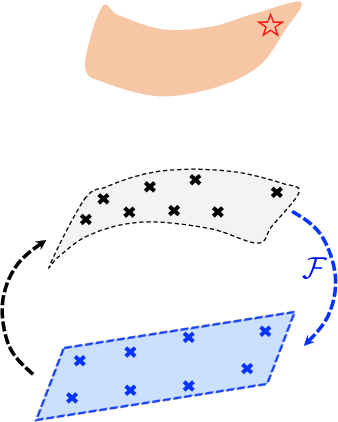
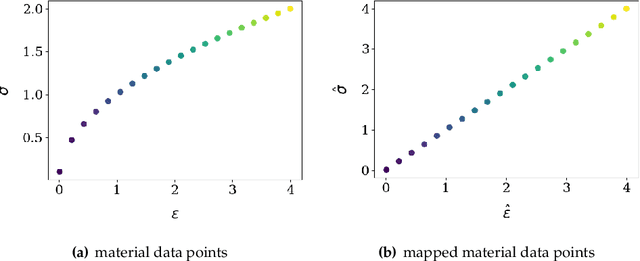
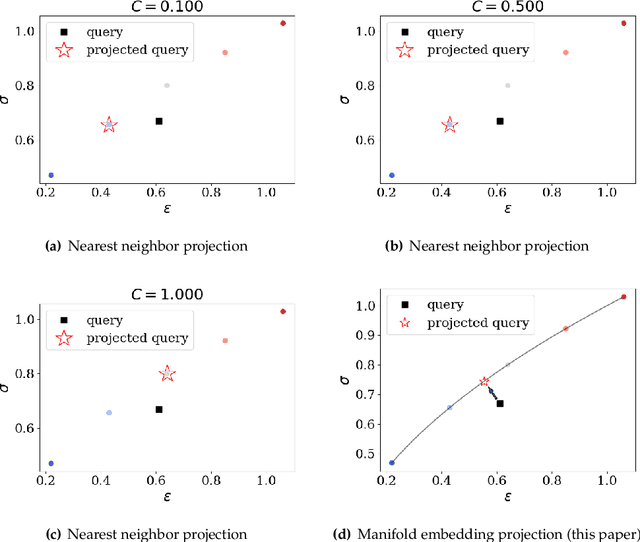
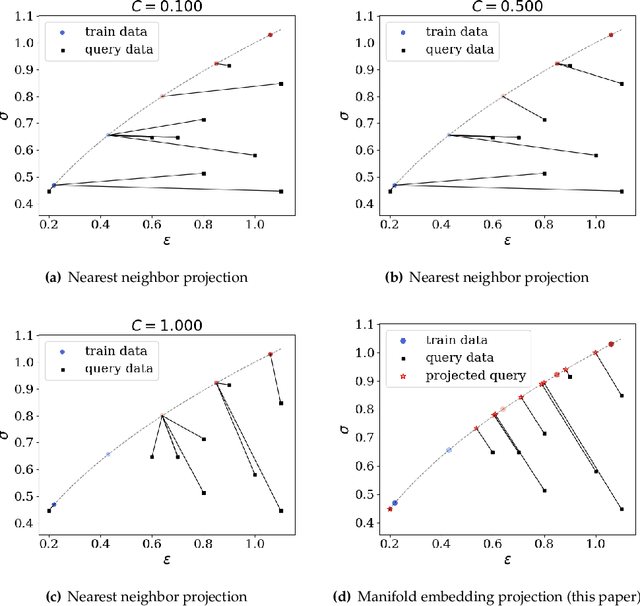
This article introduces a new data-driven approach that leverages a manifold embedding generated by the invertible neural network to improve the robustness, efficiency, and accuracy of the constitutive-law-free simulations with limited data. We achieve this by training a deep neural network to globally map data from the constitutive manifold onto a lower-dimensional Euclidean vector space. As such, we establish the relation between the norm of the mapped Euclidean vector space and the metric of the manifold and lead to a more physically consistent notion of distance for the material data. This treatment in return allows us to bypass the expensive combinatorial optimization, which may significantly speed up the model-free simulations when data are abundant and of high dimensions. Meanwhile, the learning of embedding also improves the robustness of the algorithm when the data is sparse or distributed unevenly in the parametric space. Numerical experiments are provided to demonstrate and measure the performance of the manifold embedding technique under different circumstances. Results obtained from the proposed method and those obtained via the classical energy norms are compared.

MD-inferred neural network monoclinic finite-strain hyperelasticity models for $β$-HMX: Sobolev training and validation against physical constraints

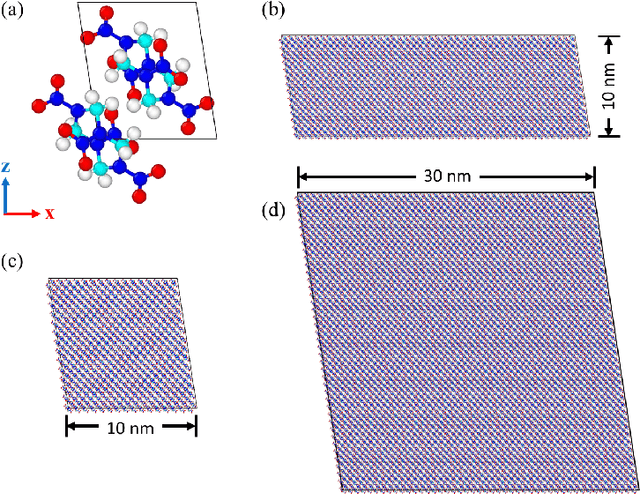
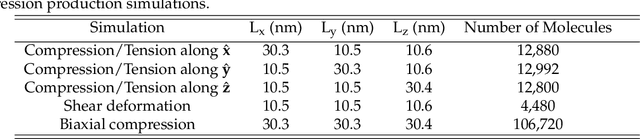
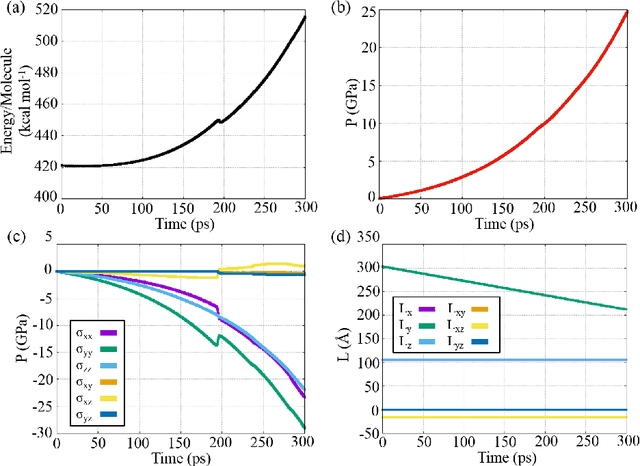
We present a machine learning framework to train and validate neural networks to predict the anisotropic elastic response of the monoclinic organic molecular crystal $\beta$-HMX in the geometrical nonlinear regime. A filtered molecular dynamic (MD) simulations database is used to train the neural networks with a Sobolev norm that uses the stress measure and a reference configuration to deduce the elastic stored energy functional. To improve the accuracy of the elasticity tangent predictions originating from the learned stored energy, a transfer learning technique is used to introduce additional tangential constraints from the data while necessary conditions (e.g. strong ellipticity, crystallographic symmetry) for the correctness of the model are either introduced as additional physical constraints or incorporated in the validation tests. Assessment of the neural networks is based on (1) the accuracy with which they reproduce the bottom-line constitutive responses predicted by MD, (2) detailed examination of their stability and uniqueness, and (3) admissibility of the predicted responses with respect to continuum mechanics theory in the finite-deformation regime. We compare the neural networks' training efficiency under different Sobolev constraints and assess the models' accuracy and robustness against MD benchmarks for $\beta$-HMX.