Equivariant geometric learning for digital rock physics: estimating formation factor and effective permeability tensors from Morse graph

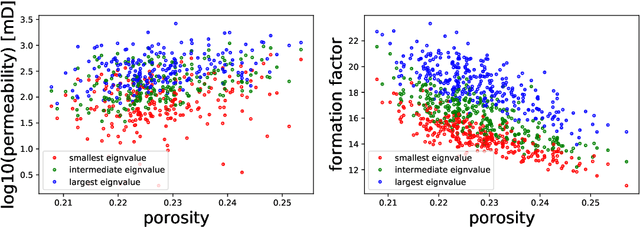
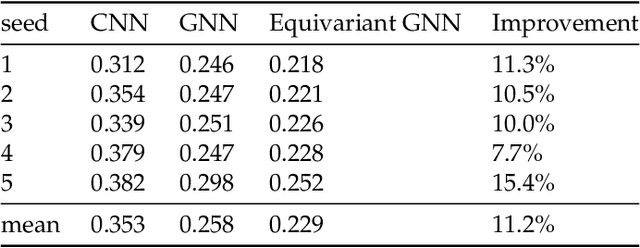
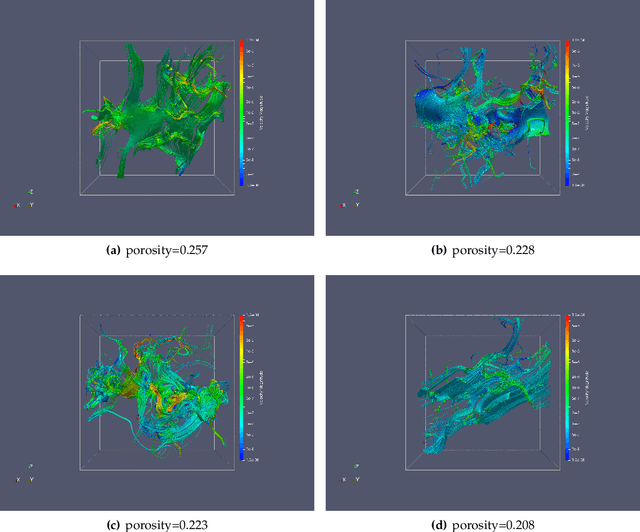
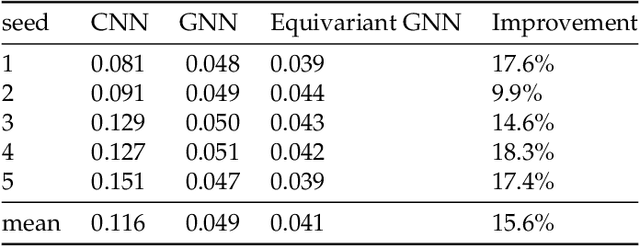
We present a SE(3)-equivariant graph neural network (GNN) approach that directly predicting the formation factor and effective permeability from micro-CT images. FFT solvers are established to compute both the formation factor and effective permeability, while the topology and geometry of the pore space are represented by a persistence-based Morse graph. Together, they constitute the database for training, validating, and testing the neural networks. While the graph and Euclidean convolutional approaches both employ neural networks to generate low-dimensional latent space to represent the features of the micro-structures for forward predictions, the SE(3) equivariant neural network is found to generate more accurate predictions, especially when the training data is limited. Numerical experiments have also shown that the new SE(3) approach leads to predictions that fulfill the material frame indifference whereas the predictions from classical convolutional neural networks (CNN) may suffer from spurious dependence on the coordinate system of the training data. Comparisons among predictions inferred from training the CNN and those from graph convolutional neural networks (GNN) with and without the equivariant constraint indicate that the equivariant graph neural network seems to perform better than the CNN and GNN without enforcing equivariant constraints.

Detection and skeletonization of single neurons and tracer injections using topological methods

Neuroscientific data analysis has traditionally relied on linear algebra and stochastic process theory. However, the tree-like shapes of neurons cannot be described easily as points in a vector space (the subtraction of two neuronal shapes is not a meaningful operation), and methods from computational topology are better suited to their analysis. Here we introduce methods from Discrete Morse (DM) Theory to extract the tree-skeletons of individual neurons from volumetric brain image data, and to summarize collections of neurons labelled by tracer injections. Since individual neurons are topologically trees, it is sensible to summarize the collection of neurons using a consensus tree-shape that provides a richer information summary than the traditional regional 'connectivity matrix' approach. The conceptually elegant DM approach lacks hand-tuned parameters and captures global properties of the data as opposed to previous approaches which are inherently local. For individual skeletonization of sparsely labelled neurons we obtain substantial performance gains over state-of-the-art non-topological methods (over 10% improvements in precision and faster proofreading). The consensus-tree summary of tracer injections incorporates the regional connectivity matrix information, but in addition captures the collective collateral branching patterns of the set of neurons connected to the injection site, and provides a bridge between single-neuron morphology and tracer-injection data.