Equivariant geometric learning for digital rock physics: estimating formation factor and effective permeability tensors from Morse graph

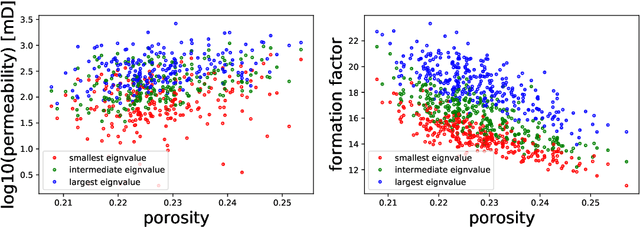
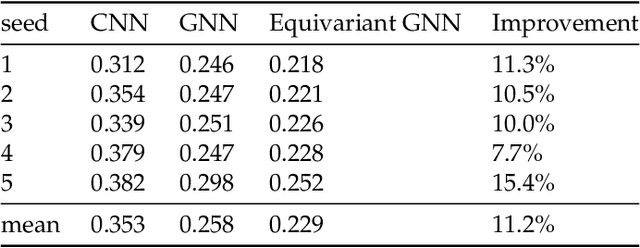
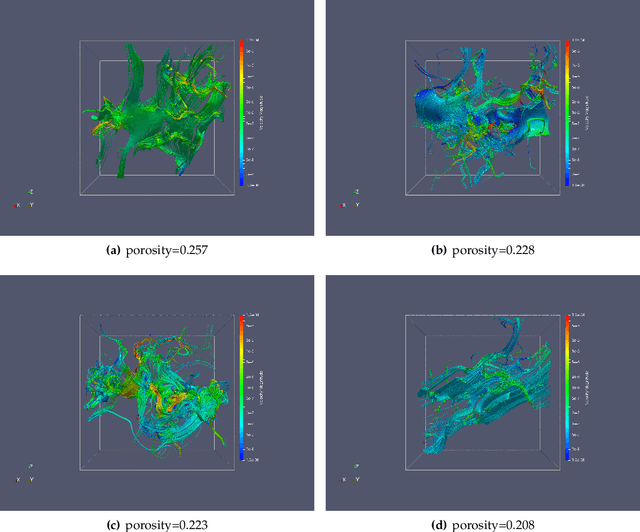
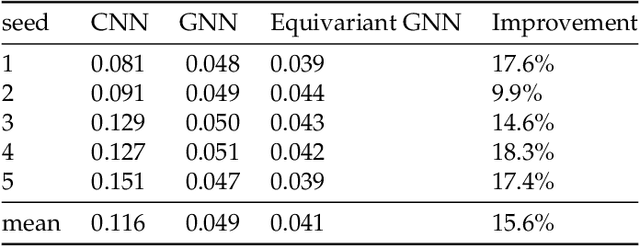
We present a SE(3)-equivariant graph neural network (GNN) approach that directly predicting the formation factor and effective permeability from micro-CT images. FFT solvers are established to compute both the formation factor and effective permeability, while the topology and geometry of the pore space are represented by a persistence-based Morse graph. Together, they constitute the database for training, validating, and testing the neural networks. While the graph and Euclidean convolutional approaches both employ neural networks to generate low-dimensional latent space to represent the features of the micro-structures for forward predictions, the SE(3) equivariant neural network is found to generate more accurate predictions, especially when the training data is limited. Numerical experiments have also shown that the new SE(3) approach leads to predictions that fulfill the material frame indifference whereas the predictions from classical convolutional neural networks (CNN) may suffer from spurious dependence on the coordinate system of the training data. Comparisons among predictions inferred from training the CNN and those from graph convolutional neural networks (GNN) with and without the equivariant constraint indicate that the equivariant graph neural network seems to perform better than the CNN and GNN without enforcing equivariant constraints.

Geometric deep learning for computational mechanics Part I: Anisotropic Hyperelasticity

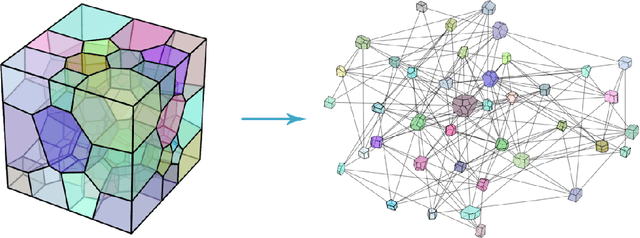
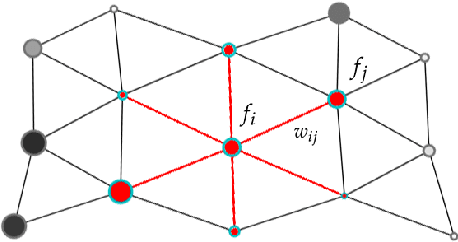
This paper is the first attempt to use geometric deep learning and Sobolev training to incorporate non-Euclidean microstructural data such that anisotropic hyperelastic material machine learning models can be trained in the finite deformation range. While traditional hyperelasticity models often incorporate homogenized measures of microstructural attributes, such as porosity averaged orientation of constitutes, these measures cannot reflect the topological structures of the attributes. We fill this knowledge gap by introducing the concept of weighted graph as a new mean to store topological information, such as the connectivity of anisotropic grains in assembles. Then, by leveraging a graph convolutional deep neural network architecture in the spectral domain, we introduce a mechanism to incorporate these non-Euclidean weighted graph data directly as input for training and for predicting the elastic responses of materials with complex microstructures. To ensure smoothness and prevent non-convexity of the trained stored energy functional, we introduce a Sobolev training technique for neural networks such that stress measure is obtained implicitly from taking directional derivatives of the trained energy functional. By optimizing the neural network to approximate both the energy functional output and the stress measure, we introduce a training procedure the improves efficiency and generalize the learned energy functional for different microstructures. The trained hybrid neural network model is then used to generate new stored energy functional for unseen microstructures in a parametric study to predict the influence of elastic anisotropy on the nucleation and propagation of fracture in the brittle regime.