Rahul Singh
Robustness Tests of NLP Machine Learning Models: Search and Semantically Replace
Apr 20, 2021
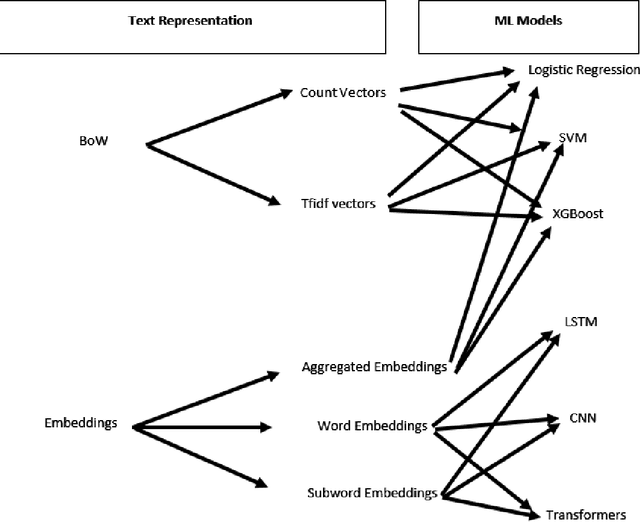
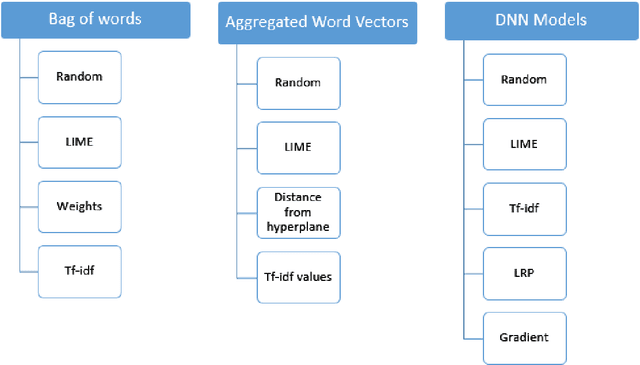
Abstract:This paper proposes a strategy to assess the robustness of different machine learning models that involve natural language processing (NLP). The overall approach relies upon a Search and Semantically Replace strategy that consists of two steps: (1) Search, which identifies important parts in the text; (2) Semantically Replace, which finds replacements for the important parts, and constrains the replaced tokens with semantically similar words. We introduce different types of Search and Semantically Replace methods designed specifically for particular types of machine learning models. We also investigate the effectiveness of this strategy and provide a general framework to assess a variety of machine learning models. Finally, an empirical comparison is provided of robustness performance among three different model types, each with a different text representation.
Debiased Kernel Methods
Feb 22, 2021Abstract:I propose a practical procedure based on bias correction and sample splitting to calculate confidence intervals for functionals of generic kernel methods, i.e. nonparametric estimators learned in a reproducing kernel Hilbert space (RKHS). For example, an analyst may desire confidence intervals for functionals of kernel ridge regression or kernel instrumental variable regression. The framework encompasses (i) evaluations over discrete domains, (ii) treatment effects of discrete treatments, and (iii) incremental treatment effects of continuous treatments. For the target quantity, whether it is (i)-(iii), I prove pointwise root-n consistency, Gaussian approximation, and semiparametric efficiency by finite sample arguments. I show that the classic assumptions of RKHS learning theory also imply inference.
Straggler-Resilient Distributed Machine Learning with Dynamic Backup Workers
Feb 11, 2021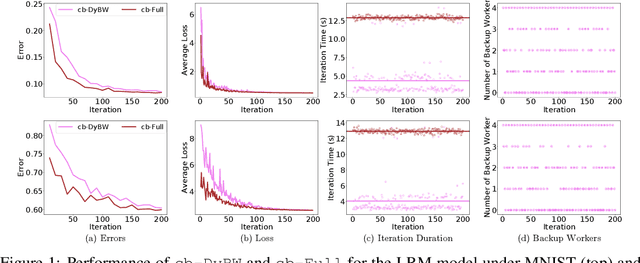

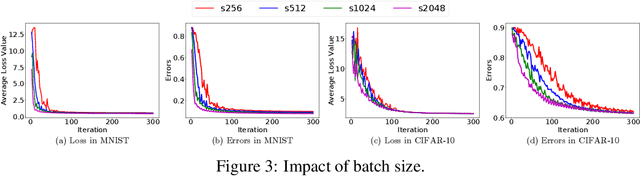
Abstract:With the increasing demand for large-scale training of machine learning models, consensus-based distributed optimization methods have recently been advocated as alternatives to the popular parameter server framework. In this paradigm, each worker maintains a local estimate of the optimal parameter vector, and iteratively updates it by waiting and averaging all estimates obtained from its neighbors, and then corrects it on the basis of its local dataset. However, the synchronization phase can be time consuming due to the need to wait for \textit{stragglers}, i.e., slower workers. An efficient way to mitigate this effect is to let each worker wait only for updates from the fastest neighbors before updating its local parameter. The remaining neighbors are called \textit{backup workers.} To minimize the globally training time over the network, we propose a fully distributed algorithm to dynamically determine the number of backup workers for each worker. We show that our algorithm achieves a linear speedup for convergence (i.e., convergence performance increases linearly with respect to the number of workers). We conduct extensive experiments on MNIST and CIFAR-10 to verify our theoretical results.
Learning Augmented Index Policy for Optimal Service Placement at the Network Edge
Jan 14, 2021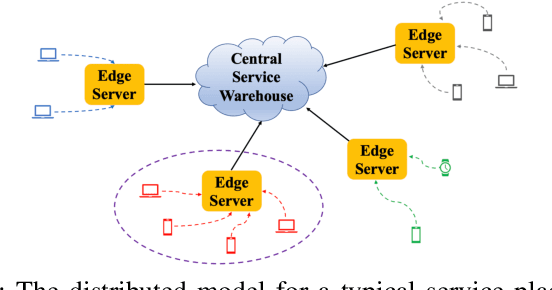
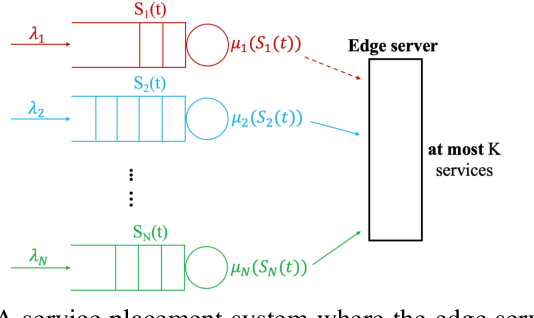
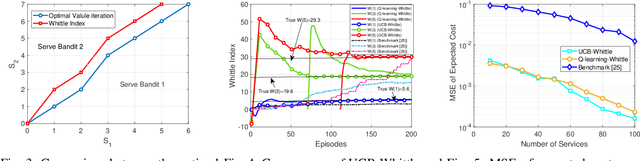

Abstract:We consider the problem of service placement at the network edge, in which a decision maker has to choose between $N$ services to host at the edge to satisfy the demands of customers. Our goal is to design adaptive algorithms to minimize the average service delivery latency for customers. We pose the problem as a Markov decision process (MDP) in which the system state is given by describing, for each service, the number of customers that are currently waiting at the edge to obtain the service. However, solving this $N$-services MDP is computationally expensive due to the curse of dimensionality. To overcome this challenge, we show that the optimal policy for a single-service MDP has an appealing threshold structure, and derive explicitly the Whittle indices for each service as a function of the number of requests from customers based on the theory of Whittle index policy. Since request arrival and service delivery rates are usually unknown and possibly time-varying, we then develop efficient learning augmented algorithms that fully utilize the structure of optimal policies with a low learning regret. The first of these is UCB-Whittle, and relies upon the principle of optimism in the face of uncertainty. The second algorithm, Q-learning-Whittle, utilizes Q-learning iterations for each service by using a two time scale stochastic approximation. We characterize the non-asymptotic performance of UCB-Whittle by analyzing its learning regret, and also analyze the convergence properties of Q-learning-Whittle. Simulation results show that the proposed policies yield excellent empirical performance.
Adversarial Estimation of Riesz Representers
Dec 30, 2020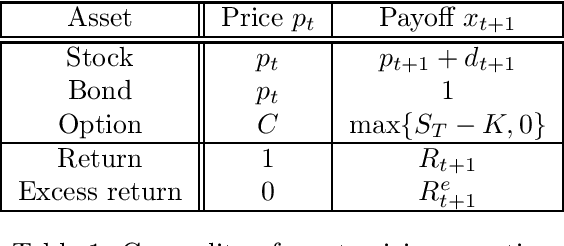
Abstract:We provide an adversarial approach to estimating Riesz representers of linear functionals within arbitrary function spaces. We prove oracle inequalities based on the localized Rademacher complexity of the function space used to approximate the Riesz representer and the approximation error. These inequalities imply fast finite sample mean-squared-error rates for many function spaces of interest, such as high-dimensional sparse linear functions, neural networks and reproducing kernel Hilbert spaces. Our approach offers a new way of estimating Riesz representers with a plethora of recently introduced machine learning techniques. We show how our estimator can be used in the context of de-biasing structural/causal parameters in semi-parametric models, for automated orthogonalization of moment equations and for estimating the stochastic discount factor in the context of asset pricing.
Kernel Methods for Unobserved Confounding: Negative Controls, Proxies, and Instruments
Dec 18, 2020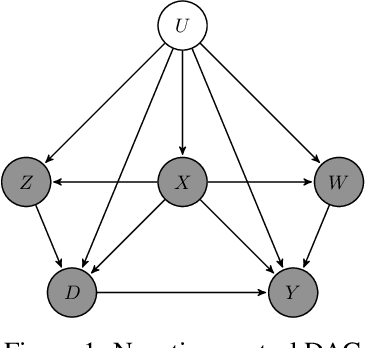
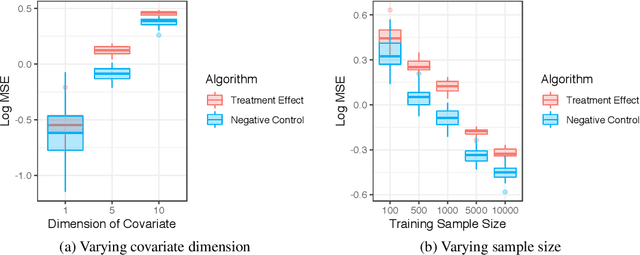
Abstract:Negative control is a strategy for learning the causal relationship between treatment and outcome in the presence of unmeasured confounding. The treatment effect can nonetheless be identified if two auxiliary variables are available: a negative control treatment (which has no effect on the actual outcome), and a negative control outcome (which is not affected by the actual treatment). These auxiliary variables can also be viewed as proxies for a traditional set of control variables, and they bear resemblance to instrumental variables. I propose a new family of non-parametric algorithms for learning treatment effects with negative controls. I consider treatment effects of the population, of sub-populations, and of alternative populations. I allow for data that may be discrete or continuous, and low-, high-, or infinite-dimensional. I impose the additional structure of the reproducing kernel Hilbert space (RKHS), a popular non-parametric setting in machine learning. I prove uniform consistency and provide finite sample rates of convergence. I evaluate the estimators in simulations.
Learning Hidden Markov Models from Aggregate Observations
Nov 23, 2020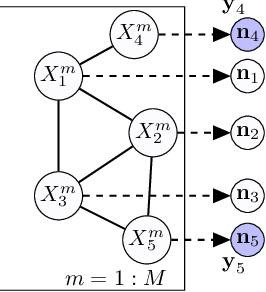
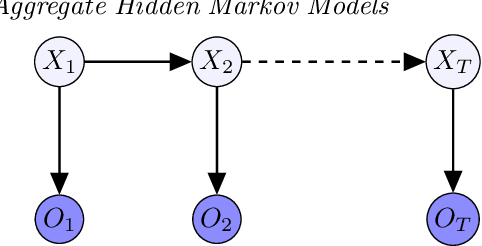
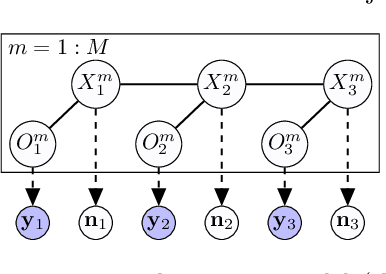
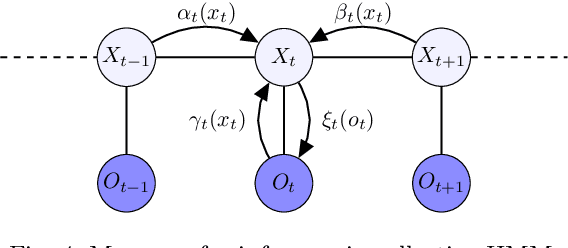
Abstract:In this paper, we propose an algorithm for estimating the parameters of a time-homogeneous hidden Markov model from aggregate observations. This problem arises when only the population level counts of the number of individuals at each time step are available, from which one seeks to learn the individual hidden Markov model. Our algorithm is built upon expectation-maximization and the recently proposed aggregate inference algorithm, the Sinkhorn belief propagation. As compared with existing methods such as expectation-maximization with non-linear belief propagation, our algorithm exhibits convergence guarantees. Moreover, our learning framework naturally reduces to the standard Baum-Welch learning algorithm when observations corresponding to a single individual are recorded. We further extend our learning algorithm to handle HMMs with continuous observations. The efficacy of our algorithm is demonstrated on a variety of datasets.
Reward Biased Maximum Likelihood Estimation for Reinforcement Learning
Nov 22, 2020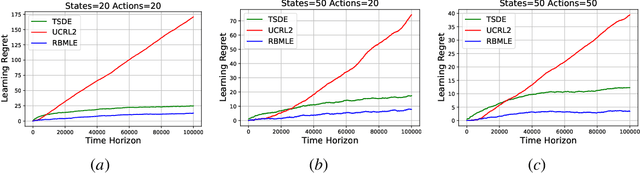
Abstract:The Reward-Biased Maximum Likelihood Estimate (RBMLE) for adaptive control of Markov chains was proposed in (Kumar and Becker, 1982) to overcome the central obstacle of what is called the "closed-identifiability problem" of adaptive control, the "dual control problem" by Feldbaum (Feldbaum, 1960a,b), or the "exploration vs. exploitation problem". It exploited the key observation that since the maximum likelihood parameter estimator can asymptotically identify the closed-transition probabilities under a certainty equivalent approach (Borkar and Varaiya, 1979), the limiting parameter estimates must necessarily have an optimal reward that is less than the optimal reward for the true but unknown system. Hence it proposed a bias in favor of parameters with larger optimal rewards, providing a carefully structured solution to above problem. It thereby proposed an optimistic approach of favoring parameters with larger optimal rewards, now known as "optimism in the face of uncertainty." The RBMLE approach has been proved to be longterm average reward optimal in a variety of contexts including controlled Markov chains, linear quadratic Gaussian systems, some nonlinear systems, and diffusions. However, modern attention is focused on the much finer notion of "regret," or finite-time performance for all time, espoused by (Lai and Robbins, 1985). Recent analysis of RBMLE for multi-armed stochastic bandits (Liu et al., 2020) and linear contextual bandits (Hung et al., 2020) has shown that it has state-of-the-art regret and exhibits empirical performance comparable to or better than the best current contenders. Motivated by this, we examine the finite-time performance of RBMLE for reinforcement learning tasks of optimal control of unknown Markov Decision Processes. We show that it has a regret of $O(\log T)$ after $T$ steps, similar to state-of-art algorithms.
Unwrapping The Black Box of Deep ReLU Networks: Interpretability, Diagnostics, and Simplification
Nov 08, 2020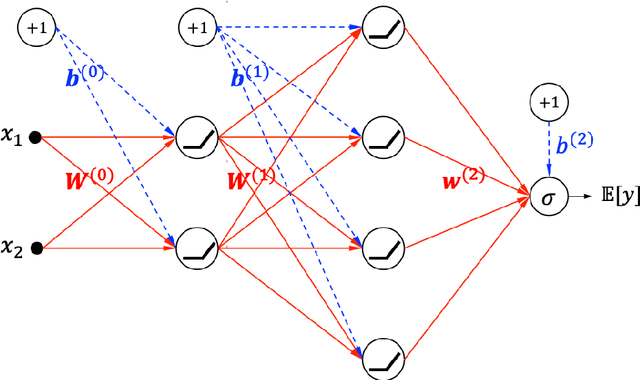

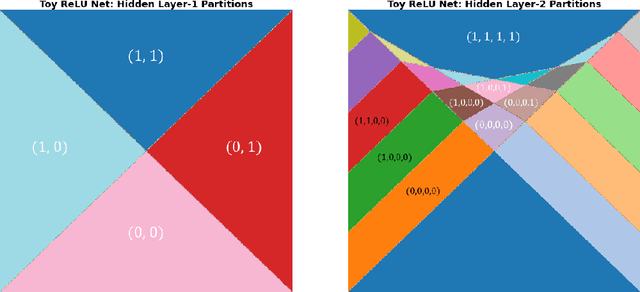
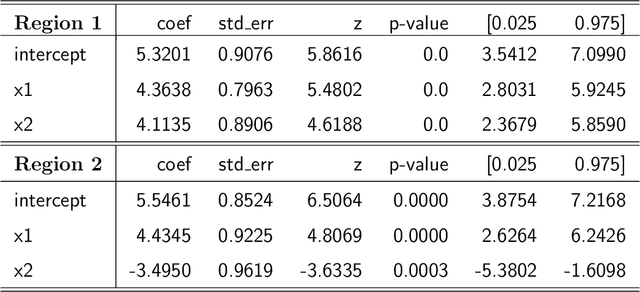
Abstract:The deep neural networks (DNNs) have achieved great success in learning complex patterns with strong predictive power, but they are often thought of as "black box" models without a sufficient level of transparency and interpretability. It is important to demystify the DNNs with rigorous mathematics and practical tools, especially when they are used for mission-critical applications. This paper aims to unwrap the black box of deep ReLU networks through local linear representation, which utilizes the activation pattern and disentangles the complex network into an equivalent set of local linear models (LLMs). We develop a convenient LLM-based toolkit for interpretability, diagnostics, and simplification of a pre-trained deep ReLU network. We propose the local linear profile plot and other visualization methods for interpretation and diagnostics, and an effective merging strategy for network simplification. The proposed methods are demonstrated by simulation examples, benchmark datasets, and a real case study in home lending credit risk assessment.
Filtering for Aggregate Hidden Markov Models with Continuous Observations
Nov 06, 2020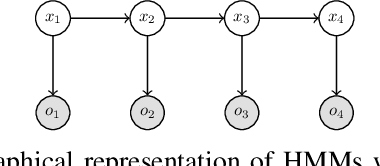
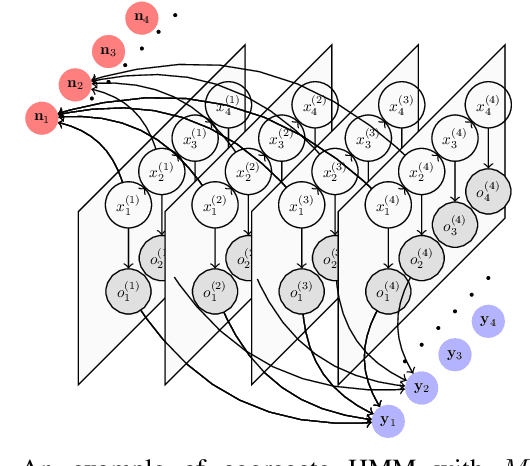
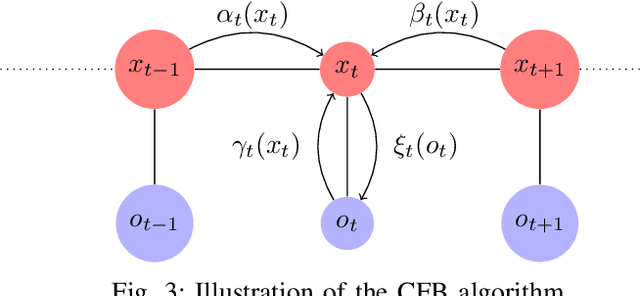
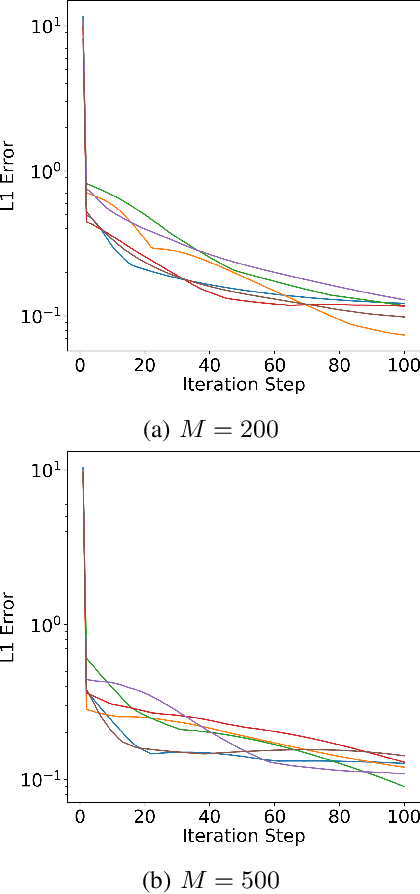
Abstract:We consider a class of filtering problems for large populations where each individual is modeled by the same hidden Markov model (HMM). In this paper, we focus on aggregate inference problems in HMMs with discrete state space and continuous observation space. The continuous observations are aggregated in a way such that the individuals are indistinguishable from measurements. We propose an aggregate inference algorithm called continuous observation collective forward-backward algorithm. It extends the recently proposed collective forward-backward algorithm for aggregate inference in HMMs with discrete observations to the case of continuous observations. The efficacy of this algorithm is illustrated through several numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge