Value-Biased Maximum Likelihood Estimation for Model-based Reinforcement Learning in Discounted Linear MDPs

We consider the infinite-horizon linear Markov Decision Processes (MDPs), where the transition probabilities of the dynamic model can be linearly parameterized with the help of a predefined low-dimensional feature mapping. While the existing regression-based approaches have been theoretically shown to achieve nearly-optimal regret, they are computationally rather inefficient due to the need for a large number of optimization runs in each time step, especially when the state and action spaces are large. To address this issue, we propose to solve linear MDPs through the lens of Value-Biased Maximum Likelihood Estimation (VBMLE), which is a classic model-based exploration principle in the adaptive control literature for resolving the well-known closed-loop identification problem of Maximum Likelihood Estimation. We formally show that (i) VBMLE enjoys $\widetilde{O}(d\sqrt{T})$ regret, where $T$ is the time horizon and $d$ is the dimension of the model parameter, and (ii) VBMLE is computationally more efficient as it only requires solving one optimization problem in each time step. In our regret analysis, we offer a generic convergence result of MLE in linear MDPs through a novel supermartingale construct and uncover an interesting connection between linear MDPs and online learning, which could be of independent interest. Finally, the simulation results show that VBMLE significantly outperforms the benchmark method in terms of both empirical regret and computation time.

Finite Time Regret Bounds for Minimum Variance Control of Autoregressive Systems with Exogenous Inputs

Minimum variance controllers have been employed in a wide-range of industrial applications. A key challenge experienced by many adaptive controllers is their poor empirical performance in the initial stages of learning. In this paper, we address the problem of initializing them so that they provide acceptable transients, and also provide an accompanying finite-time regret analysis, for adaptive minimum variance control of an auto-regressive system with exogenous inputs (ARX). Following [3], we consider a modified version of the Certainty Equivalence (CE) adaptive controller, which we call PIECE, that utilizes probing inputs for exploration. We show that it has a $C \log T$ bound on the regret after $T$ time-steps for bounded noise, and $C\log^2 T$ in the case of sub-Gaussian noise. The simulation results demonstrate the advantage of PIECE over the algorithm proposed in [3] as well as the standard Certainty Equivalence controller especially in the initial learning phase. To the best of our knowledge, this is the first work that provides finite-time regret bounds for an adaptive minimum variance controller.

Augmented RBMLE-UCB Approach for Adaptive Control of Linear Quadratic Systems

We consider the problem of controlling a stochastic linear system with quadratic costs, when its system parameters are not known to the agent -- called the adaptive LQG control problem. We re-examine an approach called "Reward-Biased Maximum Likelihood Estimate" (RBMLE) that was proposed more than forty years ago, and which predates the "Upper Confidence Bound" (UCB) method as well as the definition of "regret". It simply added a term favoring parameters with larger rewards to the estimation criterion. We propose an augmented approach that combines the penalty of the RBMLE method with the constraint of the UCB method, uniting the two approaches to optimization in the face of uncertainty. We first establish that theoretically this method retains $\mathcal{O}(\sqrt{T})$ regret, the best known so far. We show through a comprehensive simulation study that this augmented RBMLE method considerably outperforms the UCB and Thompson sampling approaches, with a regret that is typically less than 50\% of the better of their regrets. The simulation study includes all examples from earlier papers as well as a large collection of randomly generated systems.

Reward Biased Maximum Likelihood Estimation for Reinforcement Learning

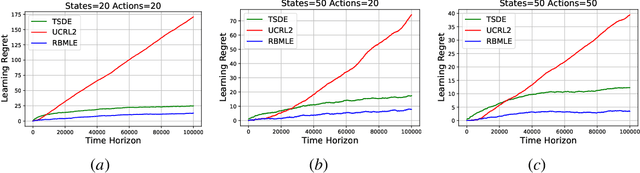
The Reward-Biased Maximum Likelihood Estimate (RBMLE) for adaptive control of Markov chains was proposed in (Kumar and Becker, 1982) to overcome the central obstacle of what is called the "closed-identifiability problem" of adaptive control, the "dual control problem" by Feldbaum (Feldbaum, 1960a,b), or the "exploration vs. exploitation problem". It exploited the key observation that since the maximum likelihood parameter estimator can asymptotically identify the closed-transition probabilities under a certainty equivalent approach (Borkar and Varaiya, 1979), the limiting parameter estimates must necessarily have an optimal reward that is less than the optimal reward for the true but unknown system. Hence it proposed a bias in favor of parameters with larger optimal rewards, providing a carefully structured solution to above problem. It thereby proposed an optimistic approach of favoring parameters with larger optimal rewards, now known as "optimism in the face of uncertainty." The RBMLE approach has been proved to be longterm average reward optimal in a variety of contexts including controlled Markov chains, linear quadratic Gaussian systems, some nonlinear systems, and diffusions. However, modern attention is focused on the much finer notion of "regret," or finite-time performance for all time, espoused by (Lai and Robbins, 1985). Recent analysis of RBMLE for multi-armed stochastic bandits (Liu et al., 2020) and linear contextual bandits (Hung et al., 2020) has shown that it has state-of-the-art regret and exhibits empirical performance comparable to or better than the best current contenders. Motivated by this, we examine the finite-time performance of RBMLE for reinforcement learning tasks of optimal control of unknown Markov Decision Processes. We show that it has a regret of $O(\log T)$ after $T$ steps, similar to state-of-art algorithms.