Source Condition Double Robust Inference on Functionals of Inverse Problems

We consider estimation of parameters defined as linear functionals of solutions to linear inverse problems. Any such parameter admits a doubly robust representation that depends on the solution to a dual linear inverse problem, where the dual solution can be thought as a generalization of the inverse propensity function. We provide the first source condition double robust inference method that ensures asymptotic normality around the parameter of interest as long as either the primal or the dual inverse problem is sufficiently well-posed, without knowledge of which inverse problem is the more well-posed one. Our result is enabled by novel guarantees for iterated Tikhonov regularized adversarial estimators for linear inverse problems, over general hypothesis spaces, which are developments of independent interest.

Minimax Instrumental Variable Regression and $L_2$ Convergence Guarantees without Identification or Closedness

In this paper, we study nonparametric estimation of instrumental variable (IV) regressions. Recently, many flexible machine learning methods have been developed for instrumental variable estimation. However, these methods have at least one of the following limitations: (1) restricting the IV regression to be uniquely identified; (2) only obtaining estimation error rates in terms of pseudometrics (\emph{e.g.,} projected norm) rather than valid metrics (\emph{e.g.,} $L_2$ norm); or (3) imposing the so-called closedness condition that requires a certain conditional expectation operator to be sufficiently smooth. In this paper, we present the first method and analysis that can avoid all three limitations, while still permitting general function approximation. Specifically, we propose a new penalized minimax estimator that can converge to a fixed IV solution even when there are multiple solutions, and we derive a strong $L_2$ error rate for our estimator under lax conditions. Notably, this guarantee only needs a widely-used source condition and realizability assumptions, but not the so-called closedness condition. We argue that the source condition and the closedness condition are inherently conflicting, so relaxing the latter significantly improves upon the existing literature that requires both conditions. Our estimator can achieve this improvement because it builds on a novel formulation of the IV estimation problem as a constrained optimization problem.

Automatic Debiased Machine Learning for Dynamic Treatment Effects

We extend the idea of automated debiased machine learning to the dynamic treatment regime. We show that the multiply robust formula for the dynamic treatment regime with discrete treatments can be re-stated in terms of a recursive Riesz representer characterization of nested mean regressions. We then apply a recursive Riesz representer estimation learning algorithm that estimates de-biasing corrections without the need to characterize how the correction terms look like, such as for instance, products of inverse probability weighting terms, as is done in prior work on doubly robust estimation in the dynamic regime. Our approach defines a sequence of loss minimization problems, whose minimizers are the mulitpliers of the de-biasing correction, hence circumventing the need for solving auxiliary propensity models and directly optimizing for the mean squared error of the target de-biasing correction.

Omitted Variable Bias in Machine Learned Causal Models

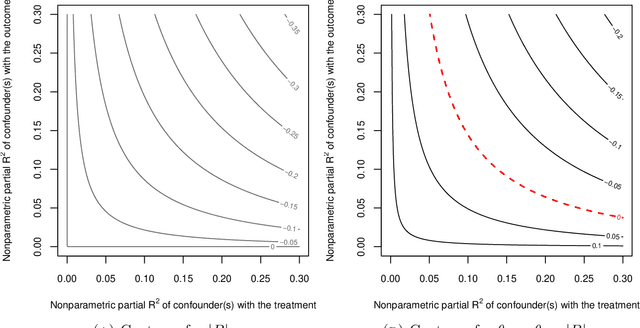
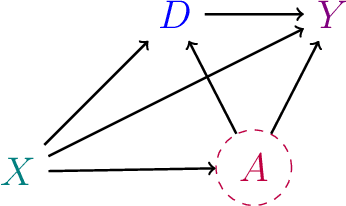
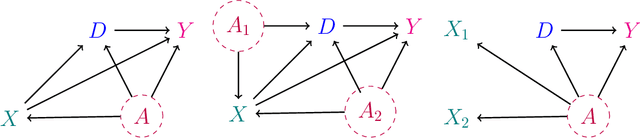
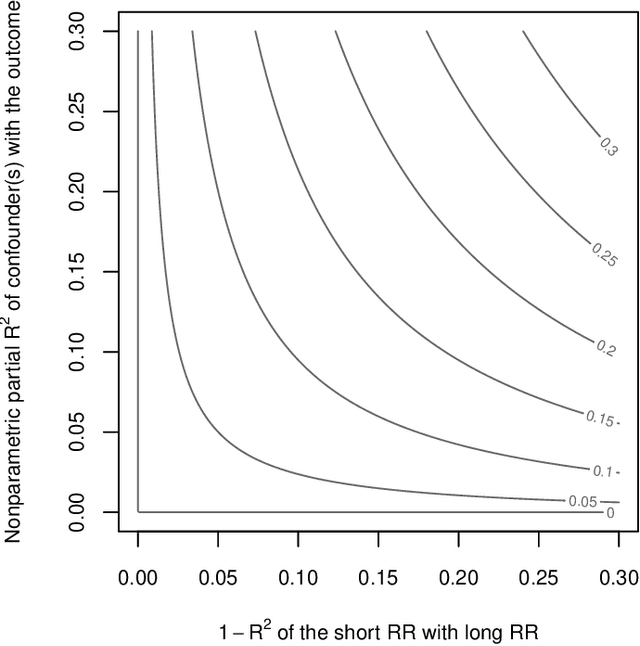
We derive general, yet simple, sharp bounds on the size of the omitted variable bias for a broad class of causal parameters that can be identified as linear functionals of the conditional expectation function of the outcome. Such functionals encompass many of the traditional targets of investigation in causal inference studies, such as, for example, (weighted) average of potential outcomes, average treatment effects (including subgroup effects, such as the effect on the treated), (weighted) average derivatives, and policy effects from shifts in covariate distribution -- all for general, nonparametric causal models. Our construction relies on the Riesz-Frechet representation of the target functional. Specifically, we show how the bound on the bias depends only on the additional variation that the latent variables create both in the outcome and in the Riesz representer for the parameter of interest. Moreover, in many important cases (e.g, average treatment effects in partially linear models, or in nonseparable models with a binary treatment) the bound is shown to depend on two easily interpretable quantities: the nonparametric partial $R^2$ (Pearson's "correlation ratio") of the unobserved variables with the treatment and with the outcome. Therefore, simple plausibility judgments on the maximum explanatory power of omitted variables (in explaining treatment and outcome variation) are sufficient to place overall bounds on the size of the bias. Finally, leveraging debiased machine learning, we provide flexible and efficient statistical inference methods to estimate the components of the bounds that are identifiable from the observed distribution.

Adversarial Estimation of Riesz Representers

We provide an adversarial approach to estimating Riesz representers of linear functionals within arbitrary function spaces. We prove oracle inequalities based on the localized Rademacher complexity of the function space used to approximate the Riesz representer and the approximation error. These inequalities imply fast finite sample mean-squared-error rates for many function spaces of interest, such as high-dimensional sparse linear functions, neural networks and reproducing kernel Hilbert spaces. Our approach offers a new way of estimating Riesz representers with a plethora of recently introduced machine learning techniques. We show how our estimator can be used in the context of de-biasing structural/causal parameters in semi-parametric models, for automated orthogonalization of moment equations and for estimating the stochastic discount factor in the context of asset pricing.

Inference on weighted average value function in high-dimensional state space

This paper gives a consistent, asymptotically normal estimator of the expected value function when the state space is high-dimensional and the first-stage nuisance functions are estimated by modern machine learning tools. First, we show that value function is orthogonal to the conditional choice probability, therefore, this nuisance function needs to be estimated only at $n^{-1/4}$ rate. Second, we give a correction term for the transition density of the state variable. The resulting orthogonal moment is robust to misspecification of the transition density and does not require this nuisance function to be consistently estimated. Third, we generalize this result by considering the weighted expected value. In this case, the orthogonal moment is doubly robust in the transition density and additional second-stage nuisance functions entering the correction term. We complete the asymptotic theory by providing bounds on second-order asymptotic terms.

Double/De-Biased Machine Learning Using Regularized Riesz Representers

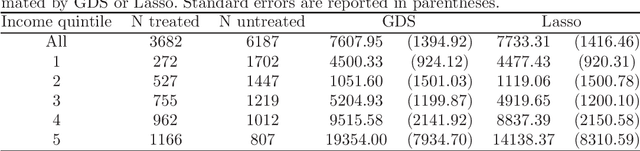
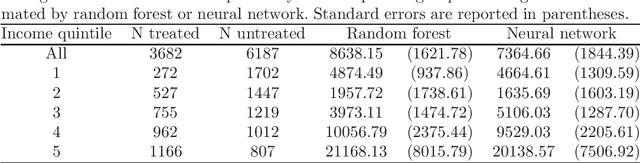
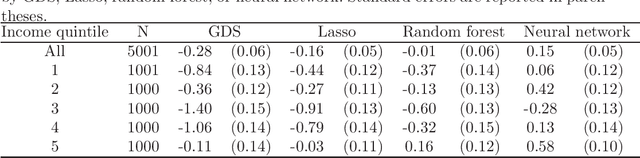
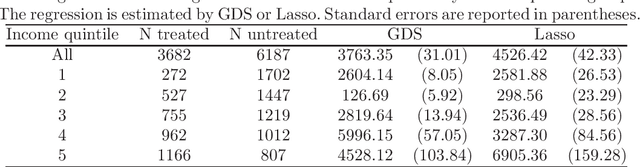
We provide adaptive inference methods for linear functionals of sparse linear approximations to the conditional expectation function. Examples of such functionals include average derivatives, policy effects, average treatment effects, and many others. The construction relies on building Neyman-orthogonal equations that are approximately invariant to perturbations of the nuisance parameters, including the Riesz representer for the linear functionals. We use L1-regularized methods to learn approximations to the regression function and the Riesz representer, and construct the estimator for the linear functionals as the solution to the orthogonal estimating equations. We establish that under weak assumptions the estimator concentrates in a 1/root n neighborhood of the target with deviations controlled by the normal laws, and the estimator attains the semi-parametric efficiency bound in many cases. In particular, either the approximation to the regression function or the approximation to the Riesz representer can be "dense" as long as one of them is sufficiently "sparse". Our main results are non-asymptotic and imply asymptotic uniform validity over large classes of models.

Double/Debiased Machine Learning for Treatment and Causal Parameters

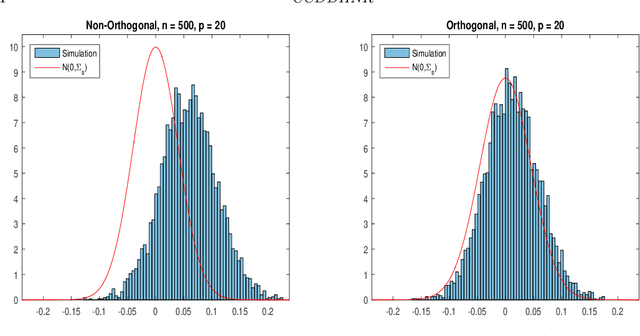
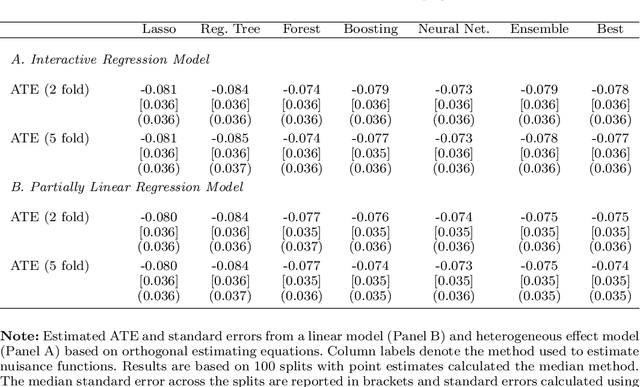
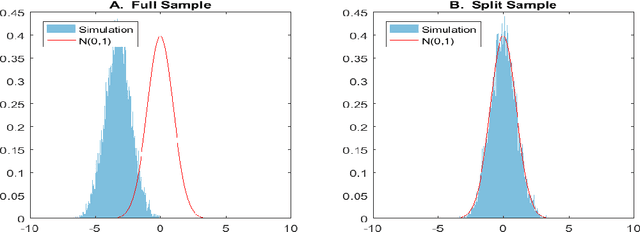
Most modern supervised statistical/machine learning (ML) methods are explicitly designed to solve prediction problems very well. Achieving this goal does not imply that these methods automatically deliver good estimators of causal parameters. Examples of such parameters include individual regression coefficients, average treatment effects, average lifts, and demand or supply elasticities. In fact, estimates of such causal parameters obtained via naively plugging ML estimators into estimating equations for such parameters can behave very poorly due to the regularization bias. Fortunately, this regularization bias can be removed by solving auxiliary prediction problems via ML tools. Specifically, we can form an orthogonal score for the target low-dimensional parameter by combining auxiliary and main ML predictions. The score is then used to build a de-biased estimator of the target parameter which typically will converge at the fastest possible 1/root(n) rate and be approximately unbiased and normal, and from which valid confidence intervals for these parameters of interest may be constructed. The resulting method thus could be called a "double ML" method because it relies on estimating primary and auxiliary predictive models. In order to avoid overfitting, our construction also makes use of the K-fold sample splitting, which we call cross-fitting. This allows us to use a very broad set of ML predictive methods in solving the auxiliary and main prediction problems, such as random forest, lasso, ridge, deep neural nets, boosted trees, as well as various hybrids and aggregators of these methods.

Double/Debiased/Neyman Machine Learning of Treatment Effects

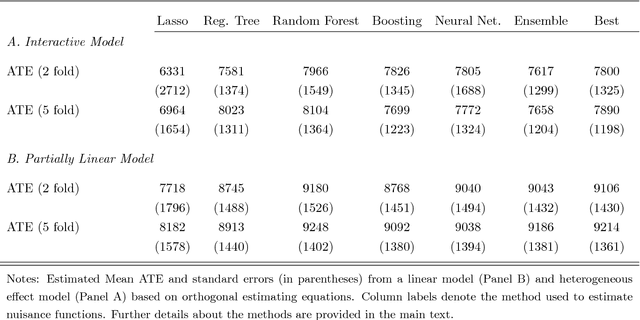
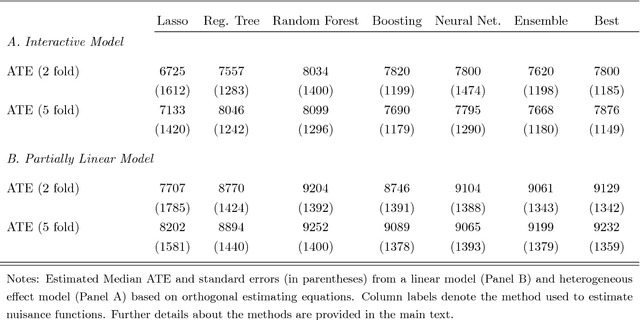
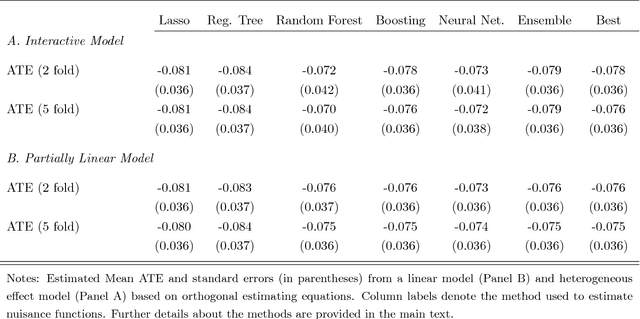
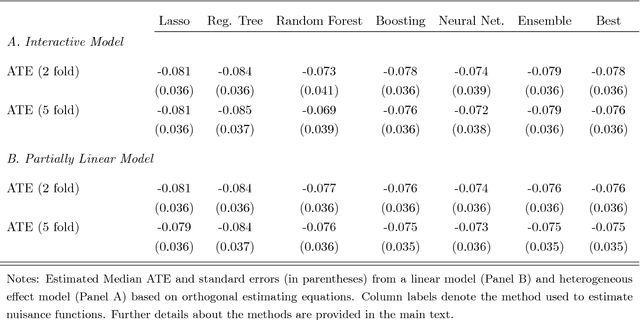
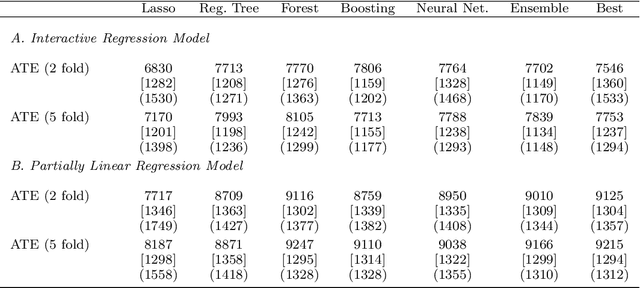
Chernozhukov, Chetverikov, Demirer, Duflo, Hansen, and Newey (2016) provide a generic double/de-biased machine learning (DML) approach for obtaining valid inferential statements about focal parameters, using Neyman-orthogonal scores and cross-fitting, in settings where nuisance parameters are estimated using a new generation of nonparametric fitting methods for high-dimensional data, called machine learning methods. In this note, we illustrate the application of this method in the context of estimating average treatment effects (ATE) and average treatment effects on the treated (ATTE) using observational data. A more general discussion and references to the existing literature are available in Chernozhukov, Chetverikov, Demirer, Duflo, Hansen, and Newey (2016).