Balancing Rewards in Text Summarization: Multi-Objective Reinforcement Learning via HyperVolume Optimization

Text summarization is a crucial task that requires the simultaneous optimization of multiple objectives, including consistency, coherence, relevance, and fluency, which presents considerable challenges. Although large language models (LLMs) have demonstrated remarkable performance, enhanced by reinforcement learning (RL), few studies have focused on optimizing the multi-objective problem of summarization through RL based on LLMs. In this paper, we introduce hypervolume optimization (HVO), a novel optimization strategy that dynamically adjusts the scores between groups during the reward process in RL by using the hypervolume method. This method guides the model's optimization to progressively approximate the pareto front, thereby generating balanced summaries across multiple objectives. Experimental results on several representative summarization datasets demonstrate that our method outperforms group relative policy optimization (GRPO) in overall scores and shows more balanced performance across different dimensions. Moreover, a 7B foundation model enhanced by HVO performs comparably to GPT-4 in the summarization task, while maintaining a shorter generation length. Our code is publicly available at https://github.com/ai4business-LiAuto/HVO.git

Multimodal Remote Inference

We consider a remote inference system with multiple modalities, where a multimodal machine learning (ML) model performs real-time inference using features collected from remote sensors. As sensor observations may change dynamically over time, fresh features are critical for inference tasks. However, timely delivering features from all modalities is often infeasible due to limited network resources. To this end, we study a two-modality scheduling problem to minimize the ML model's inference error, which is expressed as a penalty function of AoI for both modalities. We develop an index-based threshold policy and prove its optimality. Specifically, the scheduler switches modalities when the current modality's index function exceeds a threshold. We show that the two modalities share the same threshold, and both the index functions and the threshold can be computed efficiently. The optimality of our policy holds for (i) general AoI functions that are \emph{non-monotonic} and \emph{non-additive} and (ii) \emph{heterogeneous} transmission times. Numerical results show that our policy reduces inference error by up to 55% compared to round-robin and uniform random policies, which are oblivious to the AoI-based inference error function. Our results shed light on how to improve remote inference accuracy by optimizing task-oriented AoI functions.

Send Pilot or Data? Leveraging Age of Channel State Information for Throughput Maximization

In this paper, we study the optimal timing for pilot and data transmissions to maximize effective throughput, also known as goodput, over a wireless fading channel. The receiver utilizes the received pilot signal and its Age of Information (AoI), termed the Age of Channel State Information (AoCSI), to estimate the channel state. Based on this estimation, the transmitter selects an appropriate modulation and coding scheme (MCS) to maximize goodput while ensuring compliance with a predefined block error probability constraint. Furthermore, we design an optimal pilot scheduling policy that determines whether to transmit a pilot or data at each time step, with the objective of maximizing the long-term average goodput. This problem involves a non-monotonic AoI metric optimization challenge, as the goodput function is non-monotonic with respect to AoCSI. The numerical results illustrate the performance gains achieved by the proposed policy under various SNR levels and mobility speeds.

Timely Remote Estimation with Memory at the Receiver

In this study, we consider a remote estimation system that estimates a time-varying target based on sensor data transmitted over wireless channel. Due to transmission errors, some data packets fail to reach the receiver. To mitigate this, the receiver uses a buffer to store recently received data packets, which allows for more accurate estimation from the incomplete received data. Our research focuses on optimizing the transmission scheduling policy to minimize the estimation error, which is quantified as a function of the age of information vector associated with the buffered packets. Our results show that maintaining a buffer at the receiver results in better estimation performance for non-Markovian sources.

Goal-Oriented Communications for Real-time Inference with Two-Way Delay

We design a goal-oriented communication strategy for remote inference, where an intelligent model (e.g., a pre-trained neural network) at the receiver side predicts the real-time value of a target signal based on data packets transmitted from a remote location. The inference error depends on both the Age of Information (AoI) and the length of the data packets. Previous formulations of this problem either assumed IID transmission delays with immediate feedback or focused only on monotonic relations where inference performance degrades as the input data ages. In contrast, we consider a possibly non-monotonic relationship between the inference error and AoI. We show how to minimize the expected time-average inference error under two-way delay, where the delay process can have memory. Simulation results highlight the significant benefits of adopting such a goal-oriented communication strategy for remote inference, especially under highly variable delay scenarios.

Timely Communications for Remote Inference

In this paper, we analyze the impact of data freshness on remote inference systems, where a pre-trained neural network infers a time-varying target (e.g., the locations of vehicles and pedestrians) based on features (e.g., video frames) observed at a sensing node (e.g., a camera). One might expect that the performance of a remote inference system degrades monotonically as the feature becomes stale. Using an information-theoretic analysis, we show that this is true if the feature and target data sequence can be closely approximated as a Markov chain, whereas it is not true if the data sequence is far from Markovian. Hence, the inference error is a function of Age of Information (AoI), where the function could be non-monotonic. To minimize the inference error in real-time, we propose a new "selection-from-buffer" model for sending the features, which is more general than the "generate-at-will" model used in earlier studies. In addition, we design low-complexity scheduling policies to improve inference performance. For single-source, single-channel systems, we provide an optimal scheduling policy. In multi-source, multi-channel systems, the scheduling problem becomes a multi-action restless multi-armed bandit problem. For this setting, we design a new scheduling policy by integrating Whittle index-based source selection and duality-based feature selection-from-buffer algorithms. This new scheduling policy is proven to be asymptotically optimal. These scheduling results hold for minimizing general AoI functions (monotonic or non-monotonic). Data-driven evaluations demonstrate the significant advantages of our proposed scheduling policies.

On the Monotonicity of Information Aging

In this paper, we analyze the monotonicity of information aging in a remote estimation system, where historical observations of a Gaussian autoregressive AR(p) process are used to predict its future values. We consider two widely used loss functions in estimation: (i) logarithmic loss function for maximum likelihood estimation and (ii) quadratic loss function for MMSE estimation. The estimation error of the AR(p) process is written as a generalized conditional entropy which has closed-form expressions. By using a new information-theoretic tool called $\epsilon$-Markov chain, we can evaluate the divergence of the AR(p) process from being a Markov chain. When the divergence $\epsilon$ is large, the estimation error of the AR(p) process can be far from a non-decreasing function of the Age of Information (AoI). Conversely, for small divergence $\epsilon$, the inference error is close to a non-decreasing AoI function. Each observation is a short sequence taken from the AR(p) process. As the observation sequence length increases, the parameter $\epsilon$ progressively reduces to zero, and hence the estimation error becomes a non-decreasing AoI function. These results underscore a connection between the monotonicity of information aging and the divergence of from being a Markov chain.

Learning-augmented Online Minimization of Age of Information and Transmission Costs

We consider a discrete-time system where a resource-constrained source (e.g., a small sensor) transmits its time-sensitive data to a destination over a time-varying wireless channel. Each transmission incurs a fixed transmission cost (e.g., energy cost), and no transmission results in a staleness cost represented by the Age-of-Information. The source must balance the tradeoff between transmission and staleness costs. To address this challenge, we develop a robust online algorithm to minimize the sum of transmission and staleness costs, ensuring a worst-case performance guarantee. While online algorithms are robust, they are usually overly conservative and may have a poor average performance in typical scenarios. In contrast, by leveraging historical data and prediction models, machine learning (ML) algorithms perform well in average cases. However, they typically lack worst-case performance guarantees. To achieve the best of both worlds, we design a learning-augmented online algorithm that exhibits two desired properties: (i) consistency: closely approximating the optimal offline algorithm when the ML prediction is accurate and trusted; (ii) robustness: ensuring worst-case performance guarantee even ML predictions are inaccurate. Finally, we perform extensive simulations to show that our online algorithm performs well empirically and that our learning-augmented algorithm achieves both consistency and robustness.

Hoeffding's Inequality for Markov Chains under Generalized Concentrability Condition

This paper studies Hoeffding's inequality for Markov chains under the generalized concentrability condition defined via integral probability metric (IPM). The generalized concentrability condition establishes a framework that interpolates and extends the existing hypotheses of Markov chain Hoeffding-type inequalities. The flexibility of our framework allows Hoeffding's inequality to be applied beyond the ergodic Markov chains in the traditional sense. We demonstrate the utility by applying our framework to several non-asymptotic analyses arising from the field of machine learning, including (i) a generalization bound for empirical risk minimization with Markovian samples, (ii) a finite sample guarantee for Ployak-Ruppert averaging of SGD, and (iii) a new regret bound for rested Markovian bandits with general state space.

How Does Data Freshness Affect Real-time Supervised Learning?

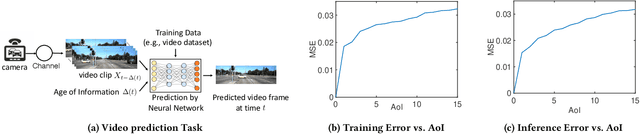
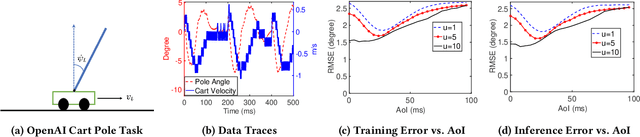
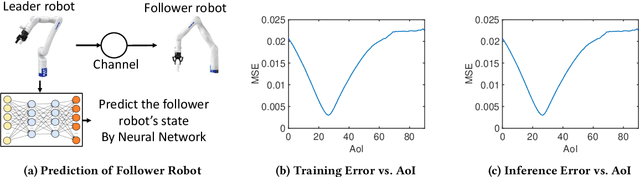
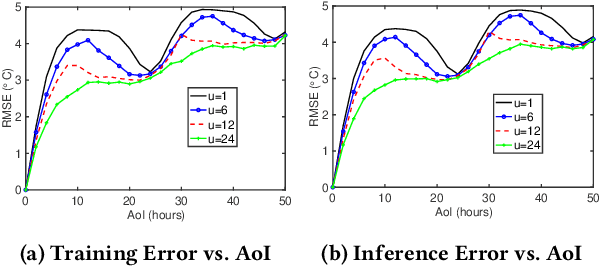
In this paper, we analyze the impact of data freshness on real-time supervised learning, where a neural network is trained to infer a time-varying target (e.g., the position of the vehicle in front) based on features (e.g., video frames) observed at a sensing node (e.g., camera or lidar). One might expect that the performance of real-time supervised learning degrades monotonically as the feature becomes stale. Using an information-theoretic analysis, we show that this is true if the feature and target data sequence can be closely approximated as a Markov chain; it is not true if the data sequence is far from Markovian. Hence, the prediction error of real-time supervised learning is a function of the Age of Information (AoI), where the function could be non-monotonic. Several experiments are conducted to illustrate the monotonic and non-monotonic behaviors of the prediction error. To minimize the inference error in real-time, we propose a new "selection-from-buffer" model for sending the features, which is more general than the "generate-at-will" model used in earlier studies. By using Gittins and Whittle indices, low-complexity scheduling strategies are developed to minimize the inference error, where a new connection between the Gittins index theory and Age of Information (AoI) minimization is discovered. These scheduling results hold (i) for minimizing general AoI functions (monotonic or non-monotonic) and (ii) for general feature transmission time distributions. Data-driven evaluations are presented to illustrate the benefits of the proposed scheduling algorithms.