Linear Convergence of Independent Natural Policy Gradient in Games with Entropy Regularization

This work focuses on the entropy-regularized independent natural policy gradient (NPG) algorithm in multi-agent reinforcement learning. In this work, agents are assumed to have access to an oracle with exact policy evaluation and seek to maximize their respective independent rewards. Each individual's reward is assumed to depend on the actions of all the agents in the multi-agent system, leading to a game between agents. We assume all agents make decisions under a policy with bounded rationality, which is enforced by the introduction of entropy regularization. In practice, a smaller regularization implies the agents are more rational and behave closer to Nash policies. On the other hand, agents with larger regularization acts more randomly, which ensures more exploration. We show that, under sufficient entropy regularization, the dynamics of this system converge at a linear rate to the quantal response equilibrium (QRE). Although regularization assumptions prevent the QRE from approximating a Nash equilibrium, our findings apply to a wide range of games, including cooperative, potential, and two-player matrix games. We also provide extensive empirical results on multiple games (including Markov games) as a verification of our theoretical analysis.

Provable Policy Gradient Methods for Average-Reward Markov Potential Games

We study Markov potential games under the infinite horizon average reward criterion. Most previous studies have been for discounted rewards. We prove that both algorithms based on independent policy gradient and independent natural policy gradient converge globally to a Nash equilibrium for the average reward criterion. To set the stage for gradient-based methods, we first establish that the average reward is a smooth function of policies and provide sensitivity bounds for the differential value functions, under certain conditions on ergodicity and the second largest eigenvalue of the underlying Markov decision process (MDP). We prove that three algorithms, policy gradient, proximal-Q, and natural policy gradient (NPG), converge to an $\epsilon$-Nash equilibrium with time complexity $O(\frac{1}{\epsilon^2})$, given a gradient/differential Q function oracle. When policy gradients have to be estimated, we propose an algorithm with $\tilde{O}(\frac{1}{\min_{s,a}\pi(a|s)\delta})$ sample complexity to achieve $\delta$ approximation error w.r.t~the $\ell_2$ norm. Equipped with the estimator, we derive the first sample complexity analysis for a policy gradient ascent algorithm, featuring a sample complexity of $\tilde{O}(1/\epsilon^5)$. Simulation studies are presented.

Provably Fast Convergence of Independent Natural Policy Gradient for Markov Potential Games

This work studies an independent natural policy gradient (NPG) algorithm for the multi-agent reinforcement learning problem in Markov potential games. It is shown that, under mild technical assumptions and the introduction of the \textit{suboptimality gap}, the independent NPG method with an oracle providing exact policy evaluation asymptotically reaches an $\epsilon$-Nash Equilibrium (NE) within $\mathcal{O}(1/\epsilon)$ iterations. This improves upon the previous best result of $\mathcal{O}(1/\epsilon^2)$ iterations and is of the same order, $\mathcal{O}(1/\epsilon)$, that is achievable for the single-agent case. Empirical results for a synthetic potential game and a congestion game are presented to verify the theoretical bounds.

Value-Biased Maximum Likelihood Estimation for Model-based Reinforcement Learning in Discounted Linear MDPs

We consider the infinite-horizon linear Markov Decision Processes (MDPs), where the transition probabilities of the dynamic model can be linearly parameterized with the help of a predefined low-dimensional feature mapping. While the existing regression-based approaches have been theoretically shown to achieve nearly-optimal regret, they are computationally rather inefficient due to the need for a large number of optimization runs in each time step, especially when the state and action spaces are large. To address this issue, we propose to solve linear MDPs through the lens of Value-Biased Maximum Likelihood Estimation (VBMLE), which is a classic model-based exploration principle in the adaptive control literature for resolving the well-known closed-loop identification problem of Maximum Likelihood Estimation. We formally show that (i) VBMLE enjoys $\widetilde{O}(d\sqrt{T})$ regret, where $T$ is the time horizon and $d$ is the dimension of the model parameter, and (ii) VBMLE is computationally more efficient as it only requires solving one optimization problem in each time step. In our regret analysis, we offer a generic convergence result of MLE in linear MDPs through a novel supermartingale construct and uncover an interesting connection between linear MDPs and online learning, which could be of independent interest. Finally, the simulation results show that VBMLE significantly outperforms the benchmark method in terms of both empirical regret and computation time.

Natural Actor-Critic for Robust Reinforcement Learning with Function Approximation

We study robust reinforcement learning (RL) with the goal of determining a well-performing policy that is robust against model mismatch between the training simulator and the testing environment. Previous policy-based robust RL algorithms mainly focus on the tabular setting under uncertainty sets that facilitate robust policy evaluation, but are no longer tractable when the number of states scales up. To this end, we propose two novel uncertainty set formulations, one based on double sampling and the other on an integral probability metric. Both make large-scale robust RL tractable even when one only has access to a simulator. We propose a robust natural actor-critic (RNAC) approach that incorporates the new uncertainty sets and employs function approximation. We provide finite-time convergence guarantees for the proposed RNAC algorithm to the optimal robust policy within the function approximation error. Finally, we demonstrate the robust performance of the policy learned by our proposed RNAC approach in multiple MuJoCo environments and a real-world TurtleBot navigation task.

Finite Time Regret Bounds for Minimum Variance Control of Autoregressive Systems with Exogenous Inputs

Minimum variance controllers have been employed in a wide-range of industrial applications. A key challenge experienced by many adaptive controllers is their poor empirical performance in the initial stages of learning. In this paper, we address the problem of initializing them so that they provide acceptable transients, and also provide an accompanying finite-time regret analysis, for adaptive minimum variance control of an auto-regressive system with exogenous inputs (ARX). Following [3], we consider a modified version of the Certainty Equivalence (CE) adaptive controller, which we call PIECE, that utilizes probing inputs for exploration. We show that it has a $C \log T$ bound on the regret after $T$ time-steps for bounded noise, and $C\log^2 T$ in the case of sub-Gaussian noise. The simulation results demonstrate the advantage of PIECE over the algorithm proposed in [3] as well as the standard Certainty Equivalence controller especially in the initial learning phase. To the best of our knowledge, this is the first work that provides finite-time regret bounds for an adaptive minimum variance controller.

Recommender system as an exploration coordinator: a bounded O(1) regret algorithm for large platforms

On typical modern platforms, users are only able to try a small fraction of the available items. This makes it difficult to model the exploration behavior of platform users as typical online learners who explore all the items. Towards addressing this issue, we propose to interpret a recommender system as a bandit exploration coordinator that provides counterfactual information updates. In particular, we introduce a novel algorithm called Counterfactual UCB (CFUCB) which is guarantees user exploration coordination with bounded regret under the presence of linear representations. Our results show that sharing information is a Subgame Perfect Nash Equilibrium for agents in terms of regret, leading to each agent achieving bounded regret. This approach has potential applications in personalized recommender systems and adaptive experimentation.

TERRA: Beam Management for Outdoor mm-Wave Networks

mm-Wave communication systems use narrow directional beams due to the spectrum's characteristic nature: high path and penetration losses. The mobile and the base station primarily employ beams in line of sight (LoS) direction and when needed in non-line of sight direction. Beam management protocol adapts the base station and mobile side beam direction during user mobility and to sustain the link during blockages. To avoid outage in transient pedestrian blockage of the LoS path, the mobile uses reflected or NLoS path available in indoor environments. Reflected paths can sustain time synchronization and maintain connectivity during temporary blockages. In outdoor environments, such reflections may not be available and prior work relied on dense base station deployment or co-ordinated multi-point access to address outage problem. Instead of dense and hence cost-intensive network deployments, we found experimentally that the mobile can capitalize on ground reflection. We developed TERRA protocol to effectively handle mobile side beam direction during transient blockage events. TERRA avoids outage during pedestrian blockages 84.5 $\%$ of the time in outdoor environments on concrete and gravel surfaces. TERRA also enables the mobile to perform a soft handover to a reserve neighbor base station in the event of a permanent blockage, without requiring any side information, unlike the existing works. Evaluations show that TERRA maintains received signal strength close to the optimal solution while keeping track of the neighbor base station.

Energy System Digitization in the Era of AI: A Three-Layered Approach towards Carbon Neutrality

The transition towards carbon-neutral electricity is one of the biggest game changers in addressing climate change since it addresses the dual challenges of removing carbon emissions from the two largest sectors of emitters: electricity and transportation. The transition to a carbon-neutral electric grid poses significant challenges to conventional paradigms of modern grid planning and operation. Much of the challenge arises from the scale of the decision making and the uncertainty associated with the energy supply and demand. Artificial Intelligence (AI) could potentially have a transformative impact on accelerating the speed and scale of carbon-neutral transition, as many decision making processes in the power grid can be cast as classic, though challenging, machine learning tasks. We point out that to amplify AI's impact on carbon-neutral transition of the electric energy systems, the AI algorithms originally developed for other applications should be tailored in three layers of technology, markets, and policy.

Anchor-Changing Regularized Natural Policy Gradient for Multi-Objective Reinforcement Learning

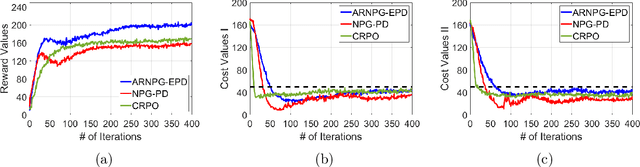
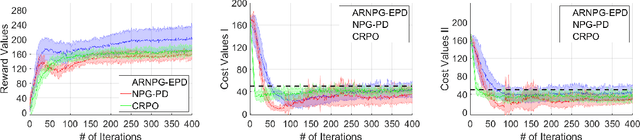
We study policy optimization for Markov decision processes (MDPs) with multiple reward value functions, which are to be jointly optimized according to given criteria such as proportional fairness (smooth concave scalarization), hard constraints (constrained MDP), and max-min trade-off. We propose an Anchor-changing Regularized Natural Policy Gradient (ARNPG) framework, which can systematically incorporate ideas from well-performing first-order methods into the design of policy optimization algorithms for multi-objective MDP problems. Theoretically, the designed algorithms based on the ARNPG framework achieve $\tilde{O}(1/T)$ global convergence with exact gradients. Empirically, the ARNPG-guided algorithms also demonstrate superior performance compared to some existing policy gradient-based approaches in both exact gradients and sample-based scenarios.