Automatic Doubly Robust Forests

This paper proposes the automatic Doubly Robust Random Forest (DRRF) algorithm for estimating the conditional expectation of a moment functional in the presence of high-dimensional nuisance functions. DRRF combines the automatic debiasing framework using the Riesz representer (Chernozhukov et al., 2022) with non-parametric, forest-based estimation methods for the conditional moment (Athey et al., 2019; Oprescu et al., 2019). In contrast to existing methods, DRRF does not require prior knowledge of the form of the debiasing term nor impose restrictive parametric or semi-parametric assumptions on the target quantity. Additionally, it is computationally efficient for making predictions at multiple query points and significantly reduces runtime compared to methods such as Orthogonal Random Forest (Oprescu et al., 2019). We establish the consistency and asymptotic normality results of DRRF estimator under general assumptions, allowing for the construction of valid confidence intervals. Through extensive simulations in heterogeneous treatment effect (HTE) estimation, we demonstrate the superior performance of DRRF over benchmark approaches in terms of estimation accuracy, robustness, and computational efficiency.

Applied Causal Inference Powered by ML and AI

An introduction to the emerging fusion of machine learning and causal inference. The book presents ideas from classical structural equation models (SEMs) and their modern AI equivalent, directed acyclical graphs (DAGs) and structural causal models (SCMs), and covers Double/Debiased Machine Learning methods to do inference in such models using modern predictive tools.

Hyperparameter Tuning for Causal Inference with Double Machine Learning: A Simulation Study

Proper hyperparameter tuning is essential for achieving optimal performance of modern machine learning (ML) methods in predictive tasks. While there is an extensive literature on tuning ML learners for prediction, there is only little guidance available on tuning ML learners for causal machine learning and how to select among different ML learners. In this paper, we empirically assess the relationship between the predictive performance of ML methods and the resulting causal estimation based on the Double Machine Learning (DML) approach by Chernozhukov et al. (2018). DML relies on estimating so-called nuisance parameters by treating them as supervised learning problems and using them as plug-in estimates to solve for the (causal) parameter. We conduct an extensive simulation study using data from the 2019 Atlantic Causal Inference Conference Data Challenge. We provide empirical insights on the role of hyperparameter tuning and other practical decisions for causal estimation with DML. First, we assess the importance of data splitting schemes for tuning ML learners within Double Machine Learning. Second, we investigate how the choice of ML methods and hyperparameters, including recent AutoML frameworks, impacts the estimation performance for a causal parameter of interest. Third, we assess to what extent the choice of a particular causal model, as characterized by incorporated parametric assumptions, can be based on predictive performance metrics.

DoubleMLDeep: Estimation of Causal Effects with Multimodal Data

This paper explores the use of unstructured, multimodal data, namely text and images, in causal inference and treatment effect estimation. We propose a neural network architecture that is adapted to the double machine learning (DML) framework, specifically the partially linear model. An additional contribution of our paper is a new method to generate a semi-synthetic dataset which can be used to evaluate the performance of causal effect estimation in the presence of text and images as confounders. The proposed methods and architectures are evaluated on the semi-synthetic dataset and compared to standard approaches, highlighting the potential benefit of using text and images directly in causal studies. Our findings have implications for researchers and practitioners in economics, marketing, finance, medicine and data science in general who are interested in estimating causal quantities using non-traditional data.

Hedonic Prices and Quality Adjusted Price Indices Powered by AI

Accurate, real-time measurements of price index changes using electronic records are essential for tracking inflation and productivity in today's economic environment. We develop empirical hedonic models that can process large amounts of unstructured product data (text, images, prices, quantities) and output accurate hedonic price estimates and derived indices. To accomplish this, we generate abstract product attributes, or ``features,'' from text descriptions and images using deep neural networks, and then use these attributes to estimate the hedonic price function. Specifically, we convert textual information about the product to numeric features using large language models based on transformers, trained or fine-tuned using product descriptions, and convert the product image to numeric features using a residual network model. To produce the estimated hedonic price function, we again use a multi-task neural network trained to predict a product's price in all time periods simultaneously. To demonstrate the performance of this approach, we apply the models to Amazon's data for first-party apparel sales and estimate hedonic prices. The resulting models have high predictive accuracy, with $R^2$ ranging from $80\%$ to $90\%$. Finally, we construct the AI-based hedonic Fisher price index, chained at the year-over-year frequency. We contrast the index with the CPI and other electronic indices.

Future-Dependent Value-Based Off-Policy Evaluation in POMDPs

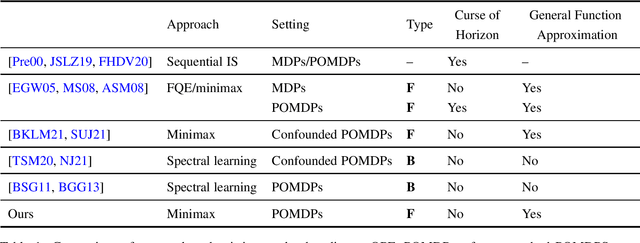
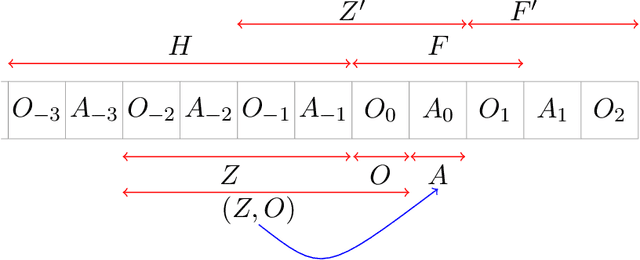
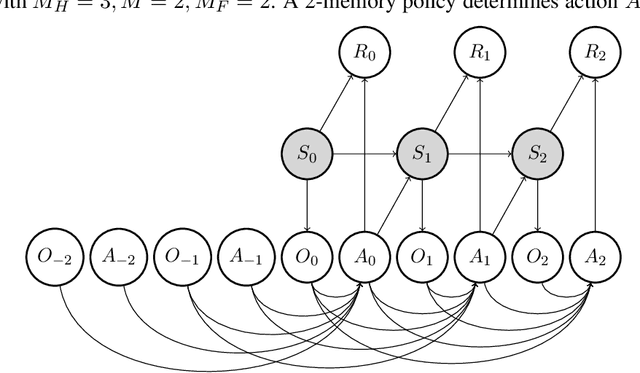
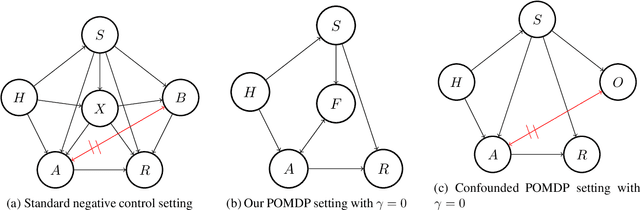
We study off-policy evaluation (OPE) for partially observable MDPs (POMDPs) with general function approximation. Existing methods such as sequential importance sampling estimators and fitted-Q evaluation suffer from the curse of horizon in POMDPs. To circumvent this problem, we develop a novel model-free OPE method by introducing future-dependent value functions that take future proxies as inputs. Future-dependent value functions play similar roles as classical value functions in fully-observable MDPs. We derive a new Bellman equation for future-dependent value functions as conditional moment equations that use history proxies as instrumental variables. We further propose a minimax learning method to learn future-dependent value functions using the new Bellman equation. We obtain the PAC result, which implies our OPE estimator is consistent as long as futures and histories contain sufficient information about latent states, and the Bellman completeness. Finally, we extend our methods to learning of dynamics and establish the connection between our approach and the well-known spectral learning methods in POMDPs.

Automatic Debiased Machine Learning for Dynamic Treatment Effects

We extend the idea of automated debiased machine learning to the dynamic treatment regime. We show that the multiply robust formula for the dynamic treatment regime with discrete treatments can be re-stated in terms of a recursive Riesz representer characterization of nested mean regressions. We then apply a recursive Riesz representer estimation learning algorithm that estimates de-biasing corrections without the need to characterize how the correction terms look like, such as for instance, products of inverse probability weighting terms, as is done in prior work on doubly robust estimation in the dynamic regime. Our approach defines a sequence of loss minimization problems, whose minimizers are the mulitpliers of the de-biasing correction, hence circumventing the need for solving auxiliary propensity models and directly optimizing for the mean squared error of the target de-biasing correction.

Omitted Variable Bias in Machine Learned Causal Models

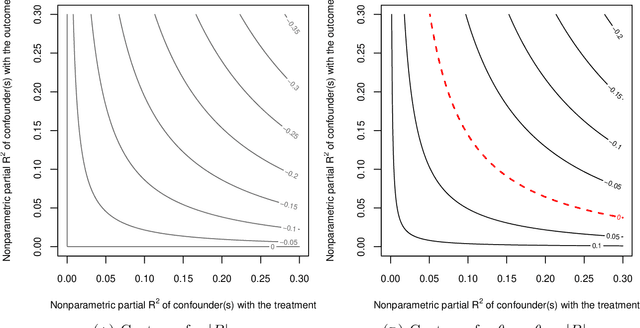
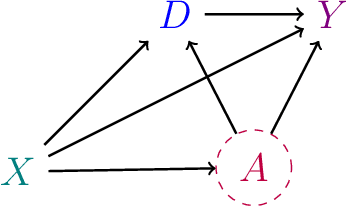
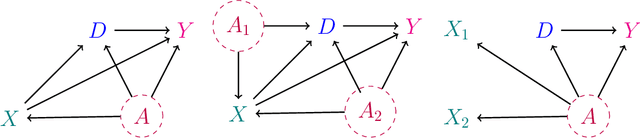
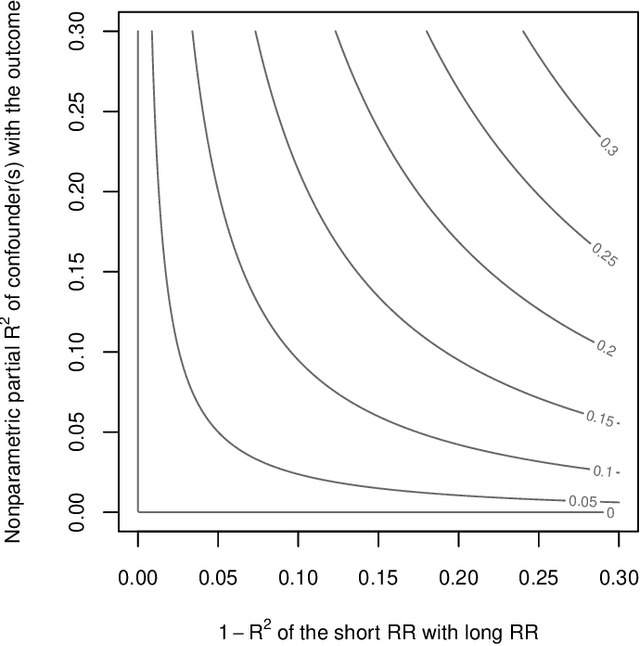
We derive general, yet simple, sharp bounds on the size of the omitted variable bias for a broad class of causal parameters that can be identified as linear functionals of the conditional expectation function of the outcome. Such functionals encompass many of the traditional targets of investigation in causal inference studies, such as, for example, (weighted) average of potential outcomes, average treatment effects (including subgroup effects, such as the effect on the treated), (weighted) average derivatives, and policy effects from shifts in covariate distribution -- all for general, nonparametric causal models. Our construction relies on the Riesz-Frechet representation of the target functional. Specifically, we show how the bound on the bias depends only on the additional variation that the latent variables create both in the outcome and in the Riesz representer for the parameter of interest. Moreover, in many important cases (e.g, average treatment effects in partially linear models, or in nonseparable models with a binary treatment) the bound is shown to depend on two easily interpretable quantities: the nonparametric partial $R^2$ (Pearson's "correlation ratio") of the unobserved variables with the treatment and with the outcome. Therefore, simple plausibility judgments on the maximum explanatory power of omitted variables (in explaining treatment and outcome variation) are sufficient to place overall bounds on the size of the bias. Finally, leveraging debiased machine learning, we provide flexible and efficient statistical inference methods to estimate the components of the bounds that are identifiable from the observed distribution.

RieszNet and ForestRiesz: Automatic Debiased Machine Learning with Neural Nets and Random Forests

Many causal and policy effects of interest are defined by linear functionals of high-dimensional or non-parametric regression functions. $\sqrt{n}$-consistent and asymptotically normal estimation of the object of interest requires debiasing to reduce the effects of regularization and/or model selection on the object of interest. Debiasing is typically achieved by adding a correction term to the plug-in estimator of the functional, that is derived based on a functional-specific theoretical derivation of what is known as the influence function and which leads to properties such as double robustness and Neyman orthogonality. We instead implement an automatic debiasing procedure based on automatically learning the Riesz representation of the linear functional using Neural Nets and Random Forests. Our method solely requires value query oracle access to the linear functional. We propose a multi-tasking Neural Net debiasing method with stochastic gradient descent minimization of a combined Riesz representer and regression loss, while sharing representation layers for the two functions. We also propose a Random Forest method which learns a locally linear representation of the Riesz function. Even though our methodology applies to arbitrary functionals, we experimentally find that it beats state of the art performance of the prior neural net based estimator of Shi et al. (2019) for the case of the average treatment effect functional. We also evaluate our method on the more challenging problem of estimating average marginal effects with continuous treatments, using semi-synthetic data of gasoline price changes on gasoline demand.

Causal Bias Quantification for Continuous Treatment

In this work we develop a novel characterization of marginal causal effect and causal bias in the continuous treatment setting. We show they can be expressed as an expectation with respect to a conditional probability distribution, which can be estimated via standard statistical and probabilistic methods. All terms in the expectations can be computed via automatic differentiation, also for highly non-linear models. We further develop a new complete criterion for identifiability of causal effects via covariate adjustment, showing the bias equals zero if the criterion is met. We study the effectiveness of our framework in three different scenarios: linear models under confounding, overcontrol and endogenous selection bias; a non-linear model where full identifiability cannot be achieved because of missing data; a simulated medical study of statins and atherosclerotic cardiovascular disease.