From Guess2Graph: When and How Can Unreliable Experts Safely Boost Causal Discovery in Finite Samples?

Causal discovery algorithms often perform poorly with limited samples. While integrating expert knowledge (including from LLMs) as constraints promises to improve performance, guarantees for existing methods require perfect predictions or uncertainty estimates, making them unreliable for practical use. We propose the Guess2Graph (G2G) framework, which uses expert guesses to guide the sequence of statistical tests rather than replacing them. This maintains statistical consistency while enabling performance improvements. We develop two instantiations of G2G: PC-Guess, which augments the PC algorithm, and gPC-Guess, a learning-augmented variant designed to better leverage high-quality expert input. Theoretically, both preserve correctness regardless of expert error, with gPC-Guess provably outperforming its non-augmented counterpart in finite samples when experts are "better than random." Empirically, both show monotonic improvement with expert accuracy, with gPC-Guess achieving significantly stronger gains.

A Classical View on Benign Overfitting: The Role of Sample Size

Benign overfitting is a phenomenon in machine learning where a model perfectly fits (interpolates) the training data, including noisy examples, yet still generalizes well to unseen data. Understanding this phenomenon has attracted considerable attention in recent years. In this work, we introduce a conceptual shift, by focusing on almost benign overfitting, where models simultaneously achieve both arbitrarily small training and test errors. This behavior is characteristic of neural networks, which often achieve low (but non-zero) training error while still generalizing well. We hypothesize that this almost benign overfitting can emerge even in classical regimes, by analyzing how the interaction between sample size and model complexity enables larger models to achieve both good training fit but still approach Bayes-optimal generalization. We substantiate this hypothesis with theoretical evidence from two case studies: (i) kernel ridge regression, and (ii) least-squares regression using a two-layer fully connected ReLU neural network trained via gradient flow. In both cases, we overcome the strong assumptions often required in prior work on benign overfitting. Our results on neural networks also provide the first generalization result in this setting that does not rely on any assumptions about the underlying regression function or noise, beyond boundedness. Our analysis introduces a novel proof technique based on decomposing the excess risk into estimation and approximation errors, interpreting gradient flow as an implicit regularizer, that helps avoid uniform convergence traps. This analysis idea could be of independent interest.

$β$-calibration of Language Model Confidence Scores for Generative QA

To use generative question-and-answering (QA) systems for decision-making and in any critical application, these systems need to provide well-calibrated confidence scores that reflect the correctness of their answers. Existing calibration methods aim to ensure that the confidence score is on average indicative of the likelihood that the answer is correct. We argue, however, that this standard (average-case) notion of calibration is difficult to interpret for decision-making in generative QA. To address this, we generalize the standard notion of average calibration and introduce $\beta$-calibration, which ensures calibration holds across different question-and-answer groups. We then propose discretized posthoc calibration schemes for achieving $\beta$-calibration.

Benign Overfitting for Regression with Trained Two-Layer ReLU Networks

We study the least-square regression problem with a two-layer fully-connected neural network, with ReLU activation function, trained by gradient flow. Our first result is a generalization result, that requires no assumptions on the underlying regression function or the noise other than that they are bounded. We operate in the neural tangent kernel regime, and our generalization result is developed via a decomposition of the excess risk into estimation and approximation errors, viewing gradient flow as an implicit regularizer. This decomposition in the context of neural networks is a novel perspective of gradient descent, and helps us avoid uniform convergence traps. In this work, we also establish that under the same setting, the trained network overfits to the data. Together, these results, establishes the first result on benign overfitting for finite-width ReLU networks for arbitrary regression functions.

Differentially Private Conditional Independence Testing

Conditional independence (CI) tests are widely used in statistical data analysis, e.g., they are the building block of many algorithms for causal graph discovery. The goal of a CI test is to accept or reject the null hypothesis that $X \perp \!\!\! \perp Y \mid Z$, where $X \in \mathbb{R}, Y \in \mathbb{R}, Z \in \mathbb{R}^d$. In this work, we investigate conditional independence testing under the constraint of differential privacy. We design two private CI testing procedures: one based on the generalized covariance measure of Shah and Peters (2020) and another based on the conditional randomization test of Cand\`es et al. (2016) (under the model-X assumption). We provide theoretical guarantees on the performance of our tests and validate them empirically. These are the first private CI tests that work for the general case when $Z$ is continuous.

Debiasing Conditional Stochastic Optimization

In this paper, we study the conditional stochastic optimization (CSO) problem which covers a variety of applications including portfolio selection, reinforcement learning, robust learning, causal inference, etc. The sample-averaged gradient of the CSO objective is biased due to its nested structure and therefore requires a high sample complexity to reach convergence. We introduce a general stochastic extrapolation technique that effectively reduces the bias. We show that for nonconvex smooth objectives, combining this extrapolation with variance reduction techniques can achieve a significantly better sample complexity than existing bounds. We also develop new algorithms for the finite-sum variant of CSO that also significantly improve upon existing results. Finally, we believe that our debiasing technique could be an interesting tool applicable to other stochastic optimization problems too.

Interventional and Counterfactual Inference with Diffusion Models

We consider the problem of answering observational, interventional, and counterfactual queries in a causally sufficient setting where only observational data and the causal graph are available. Utilizing the recent developments in diffusion models, we introduce diffusion-based causal models (DCM) to learn causal mechanisms, that generate unique latent encodings to allow for direct sampling under interventions as well as abduction for counterfactuals. We utilize DCM to model structural equations, seeing that diffusion models serve as a natural candidate here since they encode each node to a latent representation, a proxy for the exogenous noise, and offer flexible and accurate modeling to provide reliable causal statements and estimates. Our empirical evaluations demonstrate significant improvements over existing state-of-the-art methods for answering causal queries. Our theoretical results provide a methodology for analyzing the counterfactual error for general encoder/decoder models which could be of independent interest.

Thompson Sampling with Diffusion Generative Prior

In this work, we initiate the idea of using denoising diffusion models to learn priors for online decision making problems. Our special focus is on the meta-learning for bandit framework, with the goal of learning a strategy that performs well across bandit tasks of a same class. To this end, we train a diffusion model that learns the underlying task distribution and combine Thompson sampling with the learned prior to deal with new tasks at test time. Our posterior sampling algorithm is designed to carefully balance between the learned prior and the noisy observations that come from the learner's interaction with the environment. To capture realistic bandit scenarios, we also propose a novel diffusion model training procedure that trains even from incomplete and/or noisy data, which could be of independent interest. Finally, our extensive experimental evaluations clearly demonstrate the potential of the proposed approach.

Sequential Kernelized Independence Testing

Independence testing is a fundamental and classical statistical problem that has been extensively studied in the batch setting when one fixes the sample size before collecting data. However, practitioners often prefer procedures that adapt to the complexity of a problem at hand instead of setting sample size in advance. Ideally, such procedures should (a) allow stopping earlier on easy tasks (and later on harder tasks), hence making better use of available resources, and (b) continuously monitor the data and efficiently incorporate statistical evidence after collecting new data, while controlling the false alarm rate. It is well known that classical batch tests are not tailored for streaming data settings, since valid inference after data peeking requires correcting for multiple testing, but such corrections generally result in low power. In this paper, we design sequential kernelized independence tests (SKITs) that overcome such shortcomings based on the principle of testing by betting. We exemplify our broad framework using bets inspired by kernelized dependence measures such as the Hilbert-Schmidt independence criterion (HSIC) and the constrained-covariance criterion (COCO). Importantly, we also generalize the framework to non-i.i.d. time-varying settings, for which there exist no batch tests. We demonstrate the power of our approaches on both simulated and real data.

Uplifting Bandits

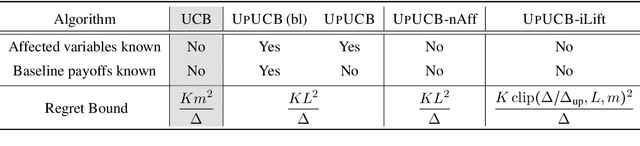
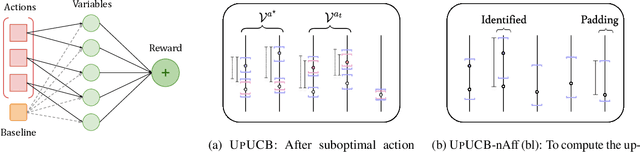
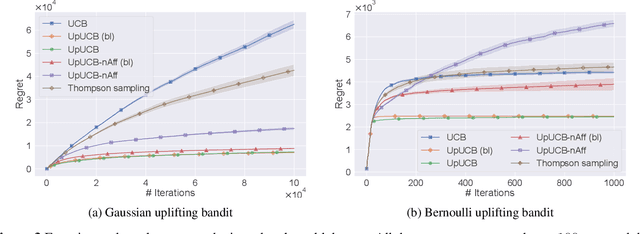
We introduce a multi-armed bandit model where the reward is a sum of multiple random variables, and each action only alters the distributions of some of them. After each action, the agent observes the realizations of all the variables. This model is motivated by marketing campaigns and recommender systems, where the variables represent outcomes on individual customers, such as clicks. We propose UCB-style algorithms that estimate the uplifts of the actions over a baseline. We study multiple variants of the problem, including when the baseline and affected variables are unknown, and prove sublinear regret bounds for all of these. We also provide lower bounds that justify the necessity of our modeling assumptions. Experiments on synthetic and real-world datasets show the benefit of methods that estimate the uplifts over policies that do not use this structure.