One-Click Upgrade from 2D to 3D: Sandwiched RGB-D Video Compression for Stereoscopic Teleconferencing

Stereoscopic video conferencing is still challenging due to the need to compress stereo RGB-D video in real-time. Though hardware implementations of standard video codecs such as H.264 / AVC and HEVC are widely available, they are not designed for stereoscopic videos and suffer from reduced quality and performance. Specific multiview or 3D extensions of these codecs are complex and lack efficient implementations. In this paper, we propose a new approach to upgrade a 2D video codec to support stereo RGB-D video compression, by wrapping it with a neural pre- and post-processor pair. The neural networks are end-to-end trained with an image codec proxy, and shown to work with a more sophisticated video codec. We also propose a geometry-aware loss function to improve rendering quality. We train the neural pre- and post-processors on a synthetic 4D people dataset, and evaluate it on both synthetic and real-captured stereo RGB-D videos. Experimental results show that the neural networks generalize well to unseen data and work out-of-box with various video codecs. Our approach saves about 30% bit-rate compared to a conventional video coding scheme and MV-HEVC at the same level of rendering quality from a novel view, without the need of a task-specific hardware upgrade.

Sandwiched Compression: Repurposing Standard Codecs with Neural Network Wrappers

We propose sandwiching standard image and video codecs between pre- and post-processing neural networks. The networks are jointly trained through a differentiable codec proxy to minimize a given rate-distortion loss. This sandwich architecture not only improves the standard codec's performance on its intended content, it can effectively adapt the codec to other types of image/video content and to other distortion measures. Essentially, the sandwich learns to transmit ``neural code images'' that optimize overall rate-distortion performance even when the overall problem is well outside the scope of the codec's design. Through a variety of examples, we apply the sandwich architecture to sources with different numbers of channels, higher resolution, higher dynamic range, and perceptual distortion measures. The results demonstrate substantial improvements (up to 9 dB gains or up to 30\% bitrate reductions) compared to alternative adaptations. We derive VQ equivalents for the sandwich, establish optimality properties, and design differentiable codec proxies approximating current standard codecs. We further analyze model complexity, visual quality under perceptual metrics, as well as sandwich configurations that offer interesting potentials in image/video compression and streaming.

Learned Nonlinear Predictor for Critically Sampled 3D Point Cloud Attribute Compression

We study 3D point cloud attribute compression via a volumetric approach: assuming point cloud geometry is known at both encoder and decoder, parameters $\theta$ of a continuous attribute function $f: \mathbb{R}^3 \mapsto \mathbb{R}$ are quantized to $\hat{\theta}$ and encoded, so that discrete samples $f_{\hat{\theta}}(\mathbf{x}_i)$ can be recovered at known 3D points $\mathbf{x}_i \in \mathbb{R}^3$ at the decoder. Specifically, we consider a nested sequences of function subspaces $\mathcal{F}^{(p)}_{l_0} \subseteq \cdots \subseteq \mathcal{F}^{(p)}_L$, where $\mathcal{F}_l^{(p)}$ is a family of functions spanned by B-spline basis functions of order $p$, $f_l^*$ is the projection of $f$ on $\mathcal{F}_l^{(p)}$ and encoded as low-pass coefficients $F_l^*$, and $g_l^*$ is the residual function in orthogonal subspace $\mathcal{G}_l^{(p)}$ (where $\mathcal{G}_l^{(p)} \oplus \mathcal{F}_l^{(p)} = \mathcal{F}_{l+1}^{(p)}$) and encoded as high-pass coefficients $G_l^*$. In this paper, to improve coding performance over [1], we study predicting $f_{l+1}^*$ at level $l+1$ given $f_l^*$ at level $l$ and encoding of $G_l^*$ for the $p=1$ case (RAHT($1$)). For the prediction, we formalize RAHT(1) linear prediction in MPEG-PCC in a theoretical framework, and propose a new nonlinear predictor using a polynomial of bilateral filter. We derive equations to efficiently compute the critically sampled high-pass coefficients $G_l^*$ amenable to encoding. We optimize parameters in our resulting feed-forward network on a large training set of point clouds by minimizing a rate-distortion Lagrangian. Experimental results show that our improved framework outperformed the MPEG G-PCC predictor by $11$ to $12\%$ in bit rate reduction.

Volumetric 3D Point Cloud Attribute Compression: Learned polynomial bilateral filter for prediction

We extend a previous study on 3D point cloud attribute compression scheme that uses a volumetric approach: given a target volumetric attribute function $f : \mathbb{R}^3 \mapsto \mathbb{R}$, we quantize and encode parameters $\theta$ that characterize $f$ at the encoder, for reconstruction $f_{\hat{\theta}}(\mathbf(x))$ at known 3D points $\mathbf(x)$ at the decoder. Specifically, parameters $\theta$ are quantized coefficients of B-spline basis vectors $\mathbf{\Phi}_l$ (for order $p \geq 2$) that span the function space $\mathcal{F}_l^{(p)}$ at a particular resolution $l$, which are coded from coarse to fine resolutions for scalability. In this work, we focus on the prediction of finer-grained coefficients given coarser-grained ones by learning parameters of a polynomial bilateral filter (PBF) from data. PBF is a pseudo-linear filter that is signal-dependent with a graph spectral interpretation common in the graph signal processing (GSP) field. We demonstrate PBF's predictive performance over a linear predictor inspired by MPEG standardization over a wide range of point cloud datasets.

Volumetric Attribute Compression for 3D Point Clouds using Feedforward Network with Geometric Attention

We study 3D point cloud attribute compression using a volumetric approach: given a target volumetric attribute function $f : \mathbb{R}^3 \rightarrow \mathbb{R}$, we quantize and encode parameter vector $\theta$ that characterizes $f$ at the encoder, for reconstruction $f_{\hat{\theta}}(\mathbf{x})$ at known 3D points $\mathbf{x}$'s at the decoder. Extending a previous work Region Adaptive Hierarchical Transform (RAHT) that employs piecewise constant functions to span a nested sequence of function spaces, we propose a feedforward linear network that implements higher-order B-spline bases spanning function spaces without eigen-decomposition. Feedforward network architecture means that the system is amenable to end-to-end neural learning. The key to our network is space-varying convolution, similar to a graph operator, whose weights are computed from the known 3D geometry for normalization. We show that the number of layers in the normalization at the encoder is equivalent to the number of terms in a matrix inverse Taylor series. Experimental results on real-world 3D point clouds show up to 2-3 dB gain over RAHT in energy compaction and 20-30% bitrate reduction.

Sandwiched Video Compression: Efficiently Extending the Reach of Standard Codecs with Neural Wrappers

We propose sandwiched video compression -- a video compression system that wraps neural networks around a standard video codec. The sandwich framework consists of a neural pre- and post-processor with a standard video codec between them. The networks are trained jointly to optimize a rate-distortion loss function with the goal of significantly improving over the standard codec in various compression scenarios. End-to-end training in this setting requires a differentiable proxy for the standard video codec, which incorporates temporal processing with motion compensation, inter/intra mode decisions, and in-loop filtering. We propose differentiable approximations to key video codec components and demonstrate that the neural codes of the sandwich lead to significantly better rate-distortion performance compared to compressing the original frames of the input video in two important scenarios. When transporting high-resolution video via low-resolution HEVC, the sandwich system obtains 6.5 dB improvements over standard HEVC. More importantly, using the well-known perceptual similarity metric, LPIPS, we observe $~30 \%$ improvements in rate at the same quality over HEVC. Last but not least we show that pre- and post-processors formed by very modestly-parameterized, light-weight networks can closely approximate these results.

Two Channel Filter Banks on Arbitrary Graphs with Positive Semi Definite Variation Operators

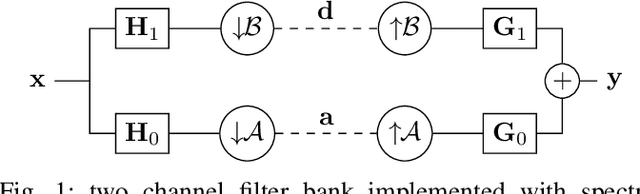
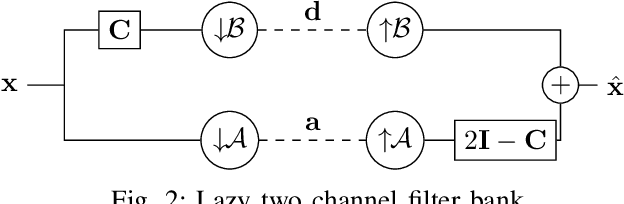
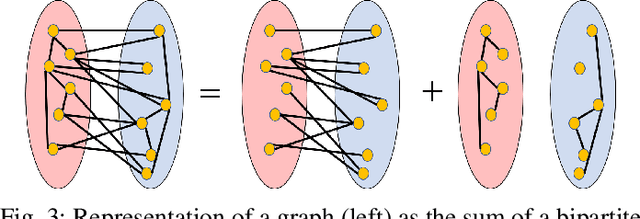
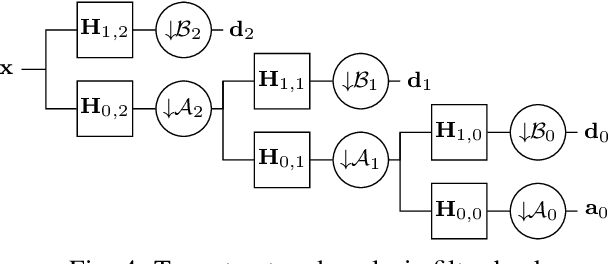
We study the design of filter banks for signals defined on the nodes of graphs. We propose novel two channel filter banks, that can be applied to arbitrary graphs, given a positive semi definite variation operator, while using downsampling operators on arbitrary vertex partitions. The proposed filter banks also satisfy several desirable properties, including perfect reconstruction, and critical sampling, while having efficient implementations. Our results generalize previous approaches only valid for the normalized Laplacian of bipartite graphs. We consider graph Fourier transforms (GFTs) given by the generalized eigenvectors of the variation operator. This GFT basis is orthogonal in an alternative inner product space, which depends on the choices of downsampling sets and variation operators. We show that the spectral folding property of the normalized Laplacian of bipartite graphs, at the core of bipartite filter bank theory, can be generalized for the proposed GFT if the inner product matrix is chosen properly. We give a probabilistic interpretation to the proposed filter banks using Gaussian graphical models. We also study orthogonality properties of tree structured filter banks, and propose a vertex partition algorithm for downsampling. We show that the proposed filter banks can be implemented efficiently on 3D point clouds, with hundreds of thousands of points (nodes), while also improving the color signal representation quality over competing state of the art approaches.

LVAC: Learned Volumetric Attribute Compression for Point Clouds using Coordinate Based Networks

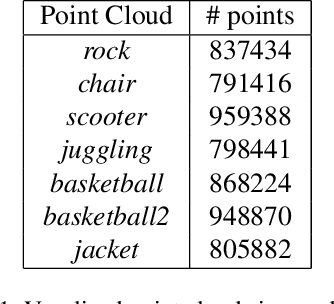
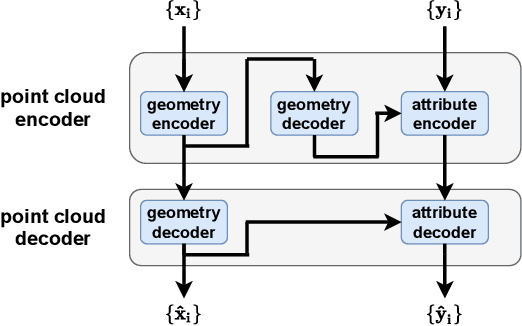
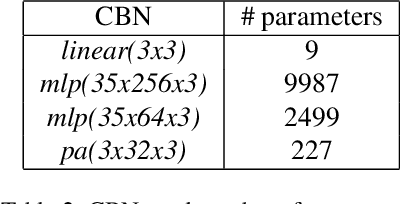
We consider the attributes of a point cloud as samples of a vector-valued volumetric function at discrete positions. To compress the attributes given the positions, we compress the parameters of the volumetric function. We model the volumetric function by tiling space into blocks, and representing the function over each block by shifts of a coordinate-based, or implicit, neural network. Inputs to the network include both spatial coordinates and a latent vector per block. We represent the latent vectors using coefficients of the region-adaptive hierarchical transform (RAHT) used in the MPEG geometry-based point cloud codec G-PCC. The coefficients, which are highly compressible, are rate-distortion optimized by back-propagation through a rate-distortion Lagrangian loss in an auto-decoder configuration. The result outperforms RAHT by 2--4 dB. This is the first work to compress volumetric functions represented by local coordinate-based neural networks. As such, we expect it to be applicable beyond point clouds, for example to compression of high-resolution neural radiance fields.

3D Scene Compression through Entropy Penalized Neural Representation Functions

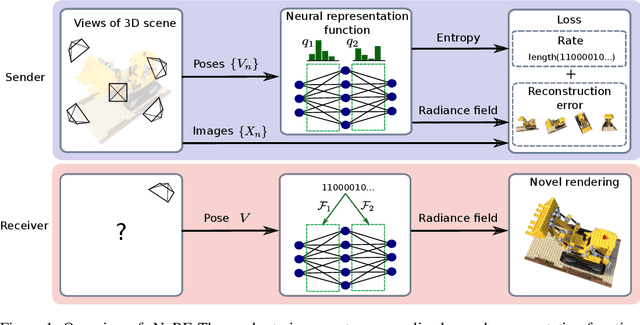
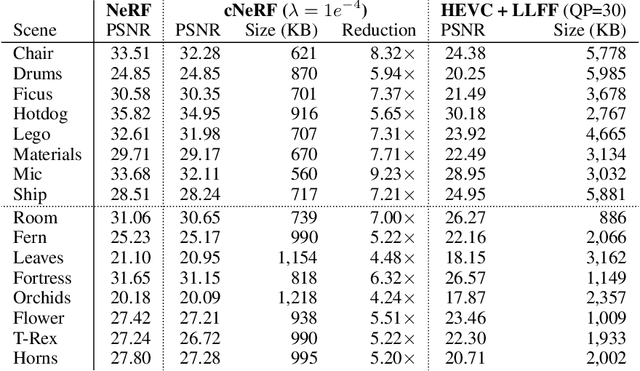
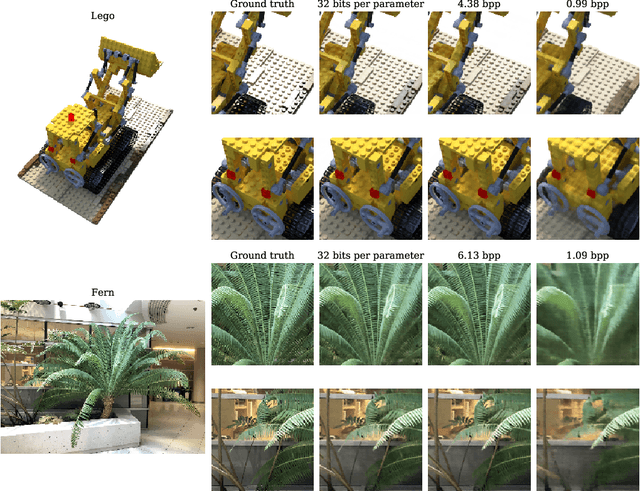
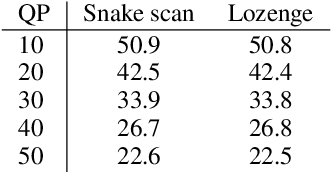
Some forms of novel visual media enable the viewer to explore a 3D scene from arbitrary viewpoints, by interpolating between a discrete set of original views. Compared to 2D imagery, these types of applications require much larger amounts of storage space, which we seek to reduce. Existing approaches for compressing 3D scenes are based on a separation of compression and rendering: each of the original views is compressed using traditional 2D image formats; the receiver decompresses the views and then performs the rendering. We unify these steps by directly compressing an implicit representation of the scene, a function that maps spatial coordinates to a radiance vector field, which can then be queried to render arbitrary viewpoints. The function is implemented as a neural network and jointly trained for reconstruction as well as compressibility, in an end-to-end manner, with the use of an entropy penalty on the parameters. Our method significantly outperforms a state-of-the-art conventional approach for scene compression, achieving simultaneously higher quality reconstructions and lower bitrates. Furthermore, we show that the performance at lower bitrates can be improved by jointly representing multiple scenes using a soft form of parameter sharing.

Deep Implicit Volume Compression

We describe a novel approach for compressing truncated signed distance fields (TSDF) stored in 3D voxel grids, and their corresponding textures. To compress the TSDF, our method relies on a block-based neural network architecture trained end-to-end, achieving state-of-the-art rate-distortion trade-off. To prevent topological errors, we losslessly compress the signs of the TSDF, which also upper bounds the reconstruction error by the voxel size. To compress the corresponding texture, we designed a fast block-based UV parameterization, generating coherent texture maps that can be effectively compressed using existing video compression algorithms. We demonstrate the performance of our algorithms on two 4D performance capture datasets, reducing bitrate by 66% for the same distortion, or alternatively reducing the distortion by 50% for the same bitrate, compared to the state-of-the-art.