A note on generalization bounds for losses with finite moments

This paper studies the truncation method from Alquier [1] to derive high-probability PAC-Bayes bounds for unbounded losses with heavy tails. Assuming that the $p$-th moment is bounded, the resulting bounds interpolate between a slow rate $1 / \sqrt{n}$ when $p=2$, and a fast rate $1 / n$ when $p \to \infty$ and the loss is essentially bounded. Moreover, the paper derives a high-probability PAC-Bayes bound for losses with a bounded variance. This bound has an exponentially better dependence on the confidence parameter and the dependency measure than previous bounds in the literature. Finally, the paper extends all results to guarantees in expectation and single-draw PAC-Bayes. In order to so, it obtains analogues of the PAC-Bayes fast rate bound for bounded losses from [2] in these settings.

A Note on the Convergence of Denoising Diffusion Probabilistic Models

Diffusion models are one of the most important families of deep generative models. In this note, we derive a quantitative upper bound on the Wasserstein distance between the data-generating distribution and the distribution learned by a diffusion model. Unlike previous works in this field, our result does not make assumptions on the learned score function. Moreover, our bound holds for arbitrary data-generating distributions on bounded instance spaces, even those without a density w.r.t. the Lebesgue measure, and the upper bound does not suffer from exponential dependencies. Our main result builds upon the recent work of Mbacke et al. (2023) and our proofs are elementary.

Semi-Counterfactual Risk Minimization Via Neural Networks

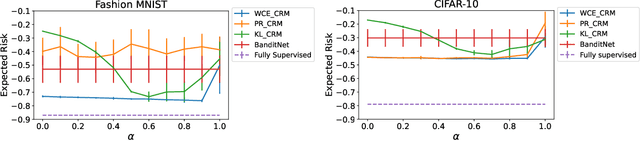
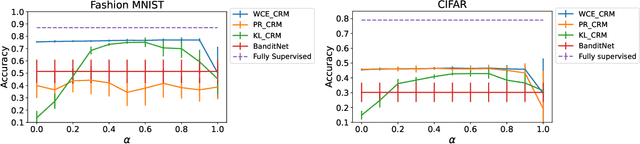
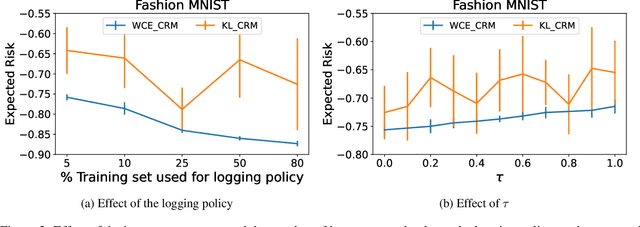
Counterfactual risk minimization is a framework for offline policy optimization with logged data which consists of context, action, propensity score, and reward for each sample point. In this work, we build on this framework and propose a learning method for settings where the rewards for some samples are not observed, and so the logged data consists of a subset of samples with unknown rewards and a subset of samples with known rewards. This setting arises in many application domains, including advertising and healthcare. While reward feedback is missing for some samples, it is possible to leverage the unknown-reward samples in order to minimize the risk, and we refer to this setting as semi-counterfactual risk minimization. To approach this kind of learning problem, we derive new upper bounds on the true risk under the inverse propensity score estimator. We then build upon these bounds to propose a regularized counterfactual risk minimization method, where the regularization term is based on the logged unknown-rewards dataset only; hence it is reward-independent. We also propose another algorithm based on generating pseudo-rewards for the logged unknown-rewards dataset. Experimental results with neural networks and benchmark datasets indicate that these algorithms can leverage the logged unknown-rewards dataset besides the logged known-reward dataset.

Progress in Self-Certified Neural Networks

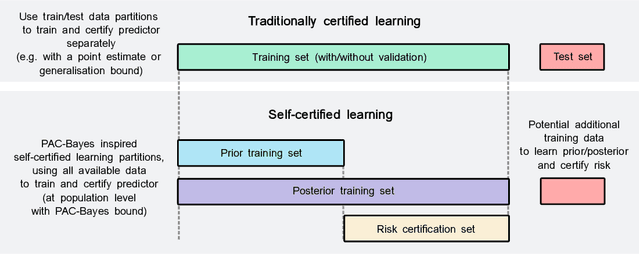
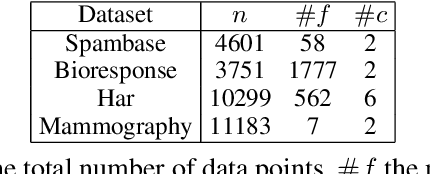
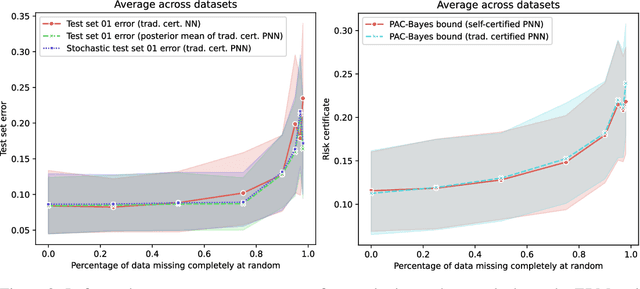
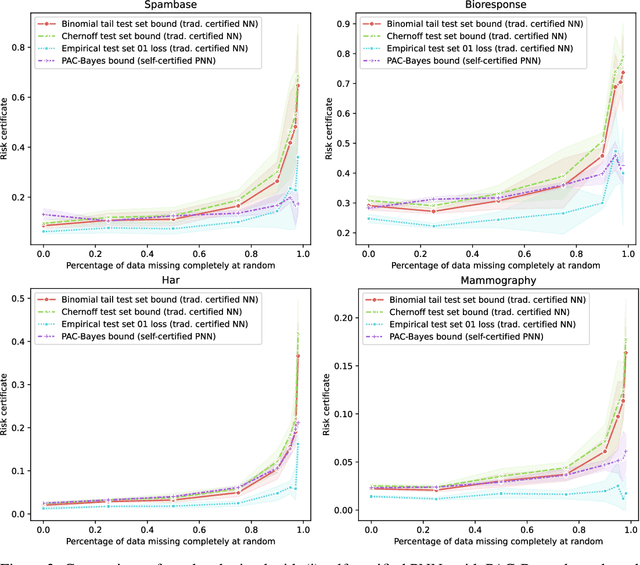
A learning method is self-certified if it uses all available data to simultaneously learn a predictor and certify its quality with a tight statistical certificate that is valid on unseen data. Recent work has shown that neural network models trained by optimising PAC-Bayes bounds lead not only to accurate predictors, but also to tight risk certificates, bearing promise towards achieving self-certified learning. In this context, learning and certification strategies based on PAC-Bayes bounds are especially attractive due to their ability to leverage all data to learn a posterior and simultaneously certify its risk with a tight numerical certificate. In this paper, we assess the progress towards self-certification in probabilistic neural networks learnt by PAC-Bayes inspired objectives. We empirically compare (on 4 classification datasets) classical test set bounds for deterministic predictors and a PAC-Bayes bound for randomised self-certified predictors. We first show that both of these generalisation bounds are not too far from out-of-sample test set errors. We then show that in data starvation regimes, holding out data for the test set bounds adversely affects generalisation performance, while self-certified strategies based on PAC-Bayes bounds do not suffer from this drawback, proving that they might be a suitable choice for the small data regime. We also find that probabilistic neural networks learnt by PAC-Bayes inspired objectives lead to certificates that can be surprisingly competitive with commonly used test set bounds.

Learning PAC-Bayes Priors for Probabilistic Neural Networks

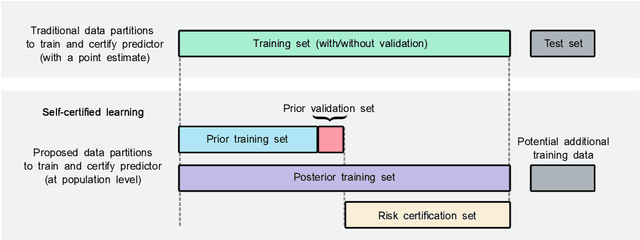
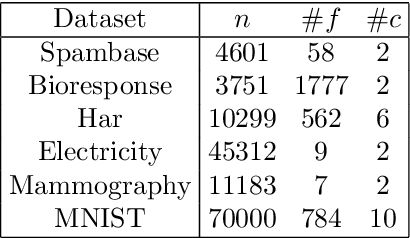
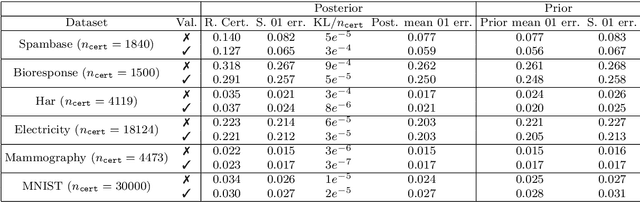
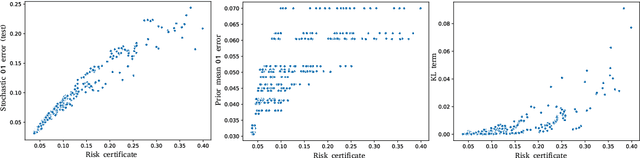
Recent works have investigated deep learning models trained by optimising PAC-Bayes bounds, with priors that are learnt on subsets of the data. This combination has been shown to lead not only to accurate classifiers, but also to remarkably tight risk certificates, bearing promise towards self-certified learning (i.e. use all the data to learn a predictor and certify its quality). In this work, we empirically investigate the role of the prior. We experiment on 6 datasets with different strategies and amounts of data to learn data-dependent PAC-Bayes priors, and we compare them in terms of their effect on test performance of the learnt predictors and tightness of their risk certificate. We ask what is the optimal amount of data which should be allocated for building the prior and show that the optimum may be dataset dependent. We demonstrate that using a small percentage of the prior-building data for validation of the prior leads to promising results. We include a comparison of underparameterised and overparameterised models, along with an empirical study of different training objectives and regularisation strategies to learn the prior distribution.

On the Role of Optimization in Double Descent: A Least Squares Study

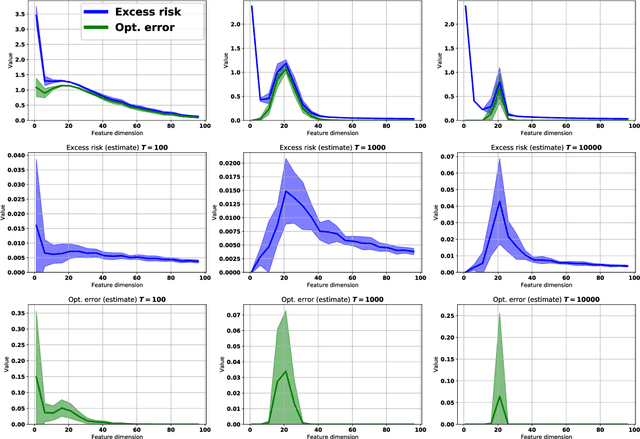
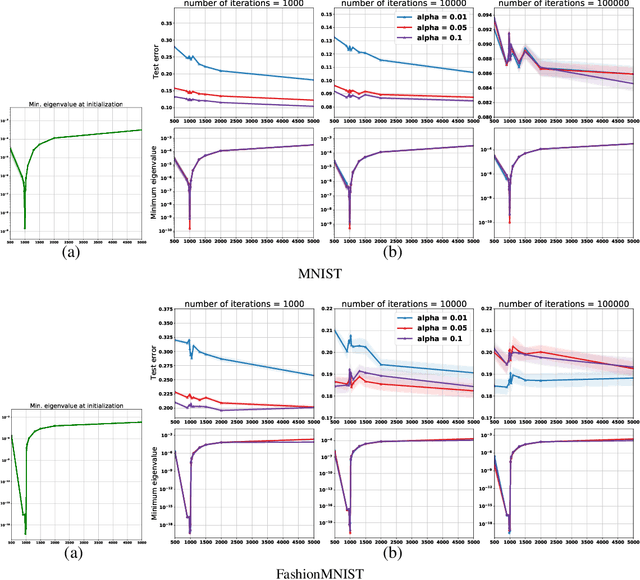
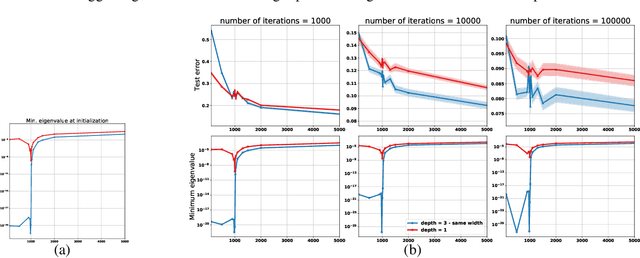
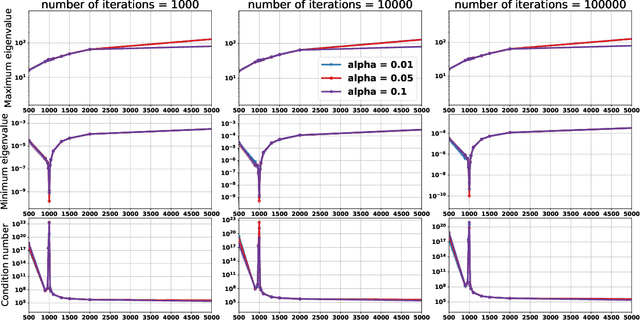
Empirically it has been observed that the performance of deep neural networks steadily improves as we increase model size, contradicting the classical view on overfitting and generalization. Recently, the double descent phenomena has been proposed to reconcile this observation with theory, suggesting that the test error has a second descent when the model becomes sufficiently overparameterized, as the model size itself acts as an implicit regularizer. In this paper we add to the growing body of work in this space, providing a careful study of learning dynamics as a function of model size for the least squares scenario. We show an excess risk bound for the gradient descent solution of the least squares objective. The bound depends on the smallest non-zero eigenvalue of the covariance matrix of the input features, via a functional form that has the double descent behavior. This gives a new perspective on the double descent curves reported in the literature. Our analysis of the excess risk allows to decouple the effect of optimization and generalization error. In particular, we find that in case of noiseless regression, double descent is explained solely by optimization-related quantities, which was missed in studies focusing on the Moore-Penrose pseudoinverse solution. We believe that our derivation provides an alternative view compared to existing work, shedding some light on a possible cause of this phenomena, at least in the considered least squares setting. We empirically explore if our predictions hold for neural networks, in particular whether the covariance of intermediary hidden activations has a similar behavior as the one predicted by our derivations.

A note on a confidence bound of Kuzborskij and Szepesvári

In an interesting recent work, Kuzborskij and Szepesv\'ari derived a confidence bound for functions of independent random variables, which is based on an inequality that relates concentration to squared perturbations of the chosen function. Kuzborskij and Szepesv\'ari also established the PAC-Bayes-ification of their confidence bound. Two important aspects of their work are that the random variables could be of unbounded range, and not necessarily of an identical distribution. The purpose of this note is to advertise/discuss these interesting results, with streamlined proofs. This expository note is written for persons who, metaphorically speaking, enjoy the "featured movie" but prefer to skip the preview sequence.

Upper and Lower Bounds on the Performance of Kernel PCA

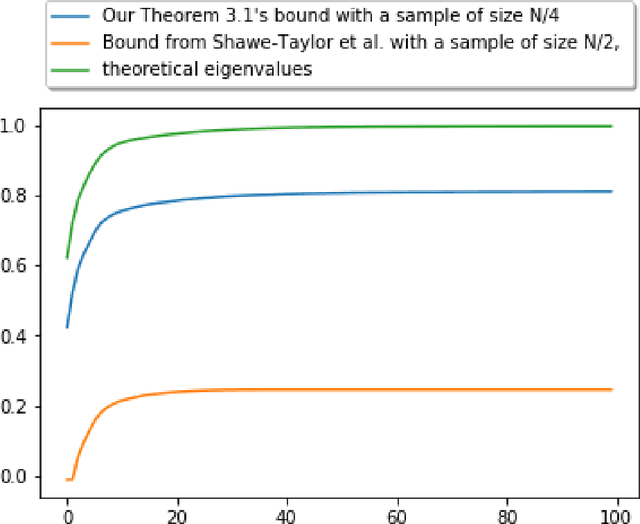
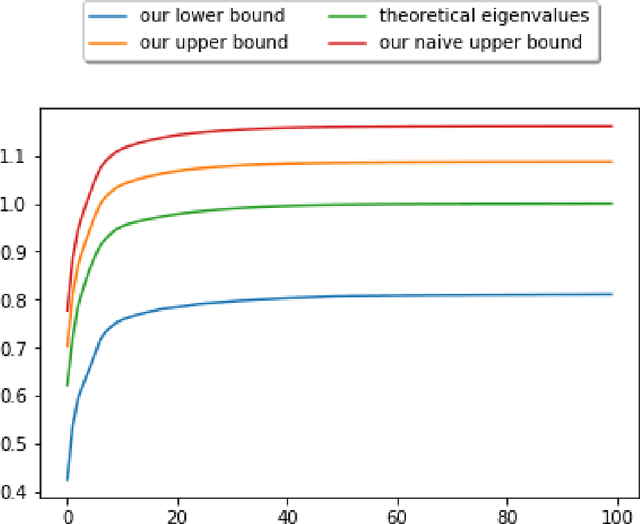
Principal Component Analysis (PCA) is a popular method for dimension reduction and has attracted an unfailing interest for decades. Recently, kernel PCA has emerged as an extension of PCA but, despite its use in practice, a sound theoretical understanding of kernel PCA is missing. In this paper, we contribute lower and upper bounds on the efficiency of kernel PCA, involving the empirical eigenvalues of the kernel Gram matrix. Two bounds are for fixed estimators, and two are for randomized estimators through the PAC-Bayes theory. We control how much information is captured by kernel PCA on average, and we dissect the bounds to highlight strengths and limitations of the kernel PCA algorithm. Therefore, we contribute to the better understanding of kernel PCA. Our bounds are briefly illustrated on a toy numerical example.

Tighter risk certificates for neural networks

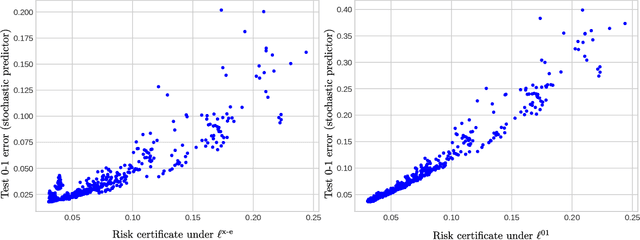
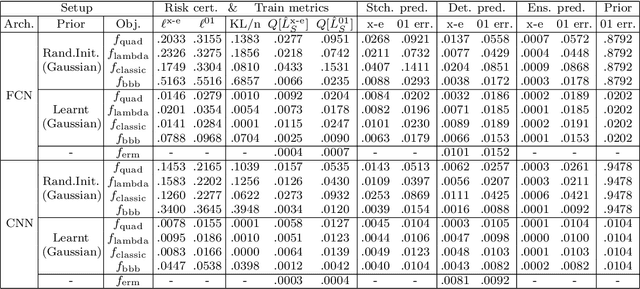
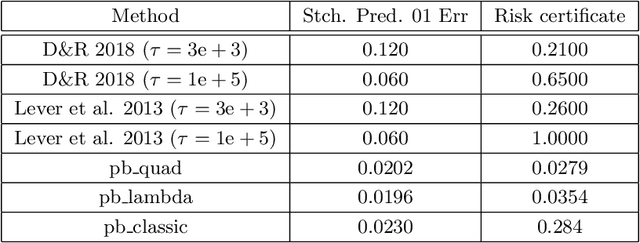
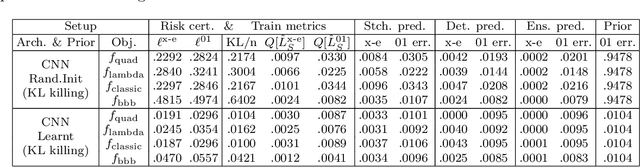
This paper presents an empirical study regarding training probabilistic neural networks using training objectives derived from PAC-Bayes bounds. In the context of probabilistic neural networks, the output of training is a probability distribution over network weights. We present two training objectives, used here for the first time in connection with training neural networks. These two training objectives are derived from tight PAC-Bayes bounds. We also re-implement a previously used training objective based on a classical PAC-Bayes bound, to compare the properties of the predictors learned using the different training objectives. We compute risk certificates that are valid on any unseen examples for the learnt predictors. We further experiment with different types of priors on the weights (both data-free and data-dependent priors) and neural network architectures. Our experiments on MNIST and CIFAR-10 show that our training methods produce competitive test set errors and non-vacuous risk bounds with much tighter values than previous results in the literature, showing promise not only to guide the learning algorithm through bounding the risk but also for model selection. These observations suggest that the methods studied here might be good candidates for self-certified learning, in the sense of certifying the risk on any unseen data without the need for data-splitting protocols.

PAC-Bayes Analysis Beyond the Usual Bounds

We focus on a stochastic learning model where the learner observes a finite set of training examples and the output of the learning process is a data-dependent distribution over a space of hypotheses. The learned data-dependent distribution is then used to make randomized predictions, and the high-level theme addressed here is guaranteeing the quality of predictions on examples that were not seen during training, i.e. generalization. In this setting the unknown quantity of interest is the expected risk of the data-dependent randomized predictor, for which upper bounds can be derived via a PAC-Bayes analysis, leading to PAC-Bayes bounds. Specifically, we present a basic PAC-Bayes inequality for stochastic kernels, from which one may derive extensions of various known PAC-Bayes bounds as well as novel bounds. We clarify the role of the requirement of fixed `data-free' priors and illustrate the use of data-dependent priors. We also present a simple bound that is valid for a loss function with unbounded range. Our analysis clarifies that those two requirements were used to upper-bound an exponential moment term, while the basic PAC-Bayes inequality remains valid with those restrictions removed.