Modeling and Forecasting COVID-19 Cases using Latent Subpopulations

Classical epidemiological models assume homogeneous populations. There have been important extensions to model heterogeneous populations, when the identity of the sub-populations is known, such as age group or geographical location. Here, we propose two new methods to model the number of people infected with COVID-19 over time, each as a linear combination of latent sub-populations -- i.e., when we do not know which person is in which sub-population, and the only available observations are the aggregates across all sub-populations. Method #1 is a dictionary-based approach, which begins with a large number of pre-defined sub-population models (each with its own starting time, shape, etc), then determines the (positive) weight of small (learned) number of sub-populations. Method #2 is a mixture-of-$M$ fittable curves, where $M$, the number of sub-populations to use, is given by the user. Both methods are compatible with any parametric model; here we demonstrate their use with first (a)~Gaussian curves and then (b)~SIR trajectories. We empirically show the performance of the proposed methods, first in (i) modeling the observed data and then in (ii) forecasting the number of infected people 1 to 4 weeks in advance. Across 187 countries, we show that the dictionary approach had the lowest mean absolute percentage error and also the lowest variance when compared with classical SIR models and moreover, it was a strong baseline that outperforms many of the models developed for COVID-19 forecasting.

Semi-Counterfactual Risk Minimization Via Neural Networks

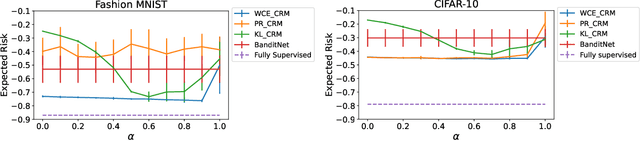
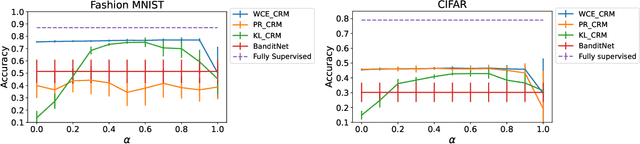
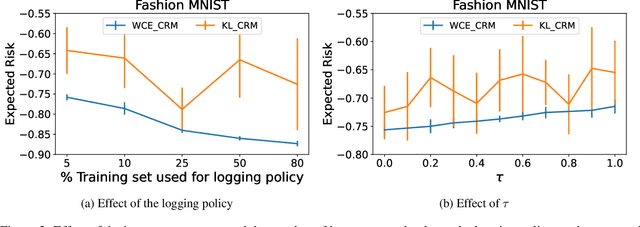
Counterfactual risk minimization is a framework for offline policy optimization with logged data which consists of context, action, propensity score, and reward for each sample point. In this work, we build on this framework and propose a learning method for settings where the rewards for some samples are not observed, and so the logged data consists of a subset of samples with unknown rewards and a subset of samples with known rewards. This setting arises in many application domains, including advertising and healthcare. While reward feedback is missing for some samples, it is possible to leverage the unknown-reward samples in order to minimize the risk, and we refer to this setting as semi-counterfactual risk minimization. To approach this kind of learning problem, we derive new upper bounds on the true risk under the inverse propensity score estimator. We then build upon these bounds to propose a regularized counterfactual risk minimization method, where the regularization term is based on the logged unknown-rewards dataset only; hence it is reward-independent. We also propose another algorithm based on generating pseudo-rewards for the logged unknown-rewards dataset. Experimental results with neural networks and benchmark datasets indicate that these algorithms can leverage the logged unknown-rewards dataset besides the logged known-reward dataset.

Domain-shift adaptation via linear transformations

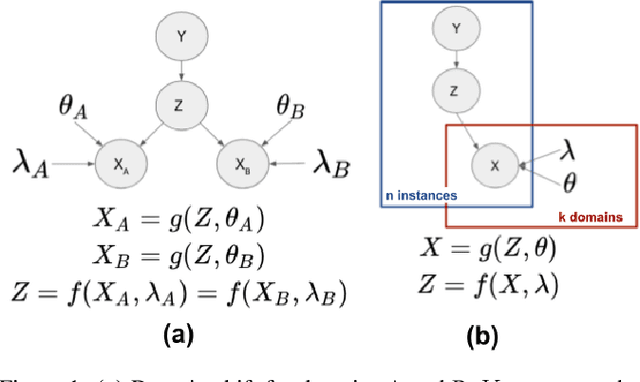
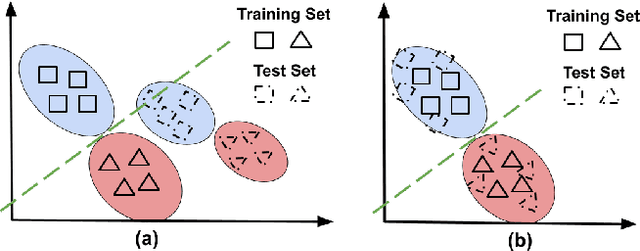
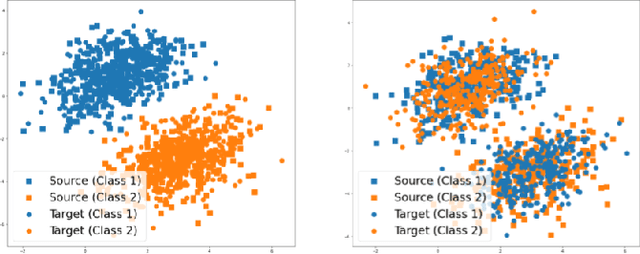
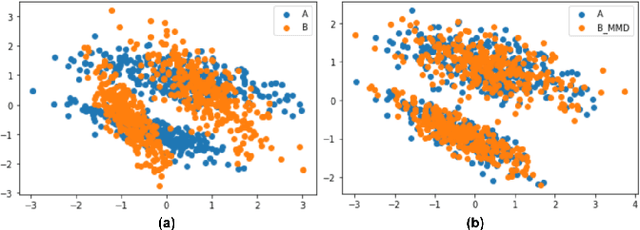
A predictor, $f_A : X \to Y$, learned with data from a source domain (A) might not be accurate on a target domain (B) when their distributions are different. Domain adaptation aims to reduce the negative effects of this distribution mismatch. Here, we analyze the case where $P_A(Y\ |\ X) \neq P_B(Y\ |\ X)$, $P_A(X) \neq P_B(X)$ but $P_A(Y) = P_B(Y)$; where there are affine transformations of $X$ that makes all distributions equivalent. We propose an approach to project the source and target domains into a lower-dimensional, common space, by (1) projecting the domains into the eigenvectors of the empirical covariance matrices of each domain, then (2) finding an orthogonal matrix that minimizes the maximum mean discrepancy between the projections of both domains. For arbitrary affine transformations, there is an inherent unidentifiability problem when performing unsupervised domain adaptation that can be alleviated in the semi-supervised case. We show the effectiveness of our approach in simulated data and in binary digit classification tasks, obtaining improvements up to 48% accuracy when correcting for the domain shift in the data.

SIMLR: Machine Learning inside the SIR model for COVID-19 Forecasting

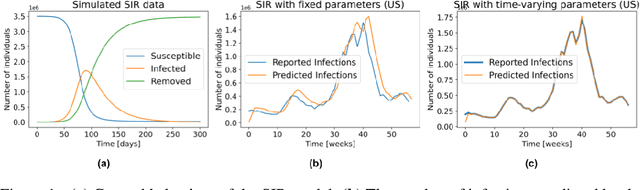
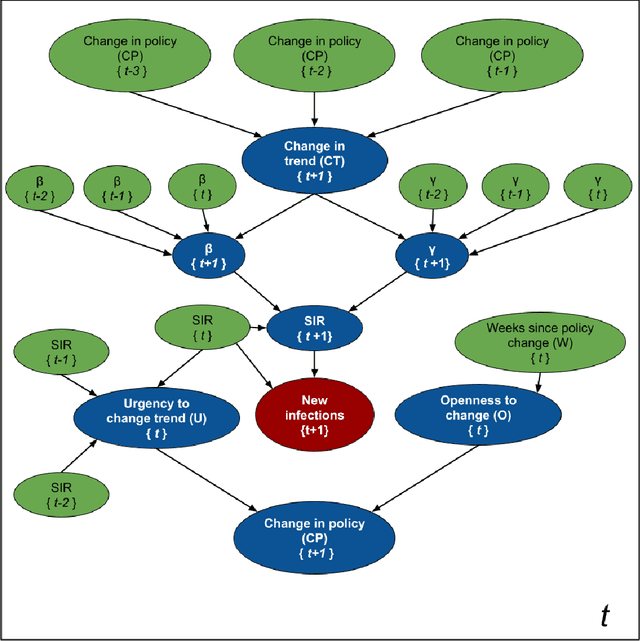
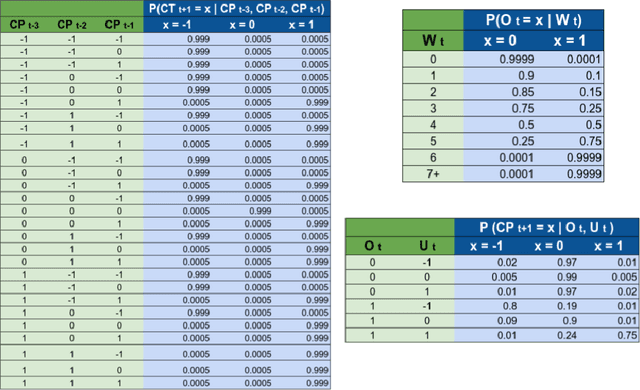
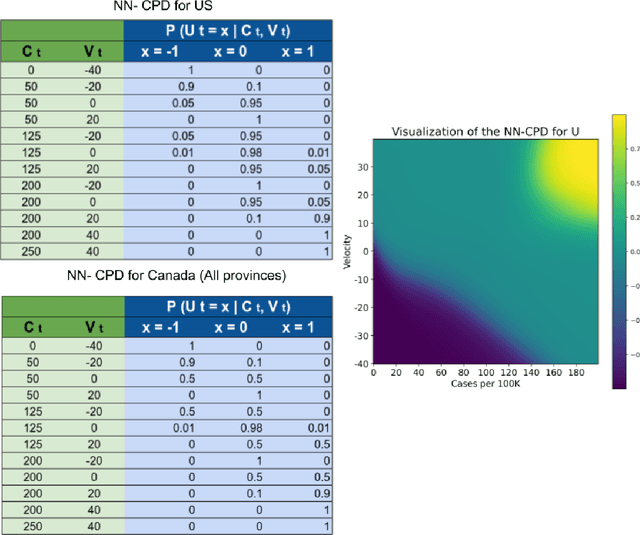
Accurate forecasts of the number of newly infected people during an epidemic are critical for making effective timely decisions. This paper addresses this challenge using the SIMLR model, which incorporates machine learning (ML) into the epidemiological SIR model. For each region, SIMLR tracks the changes in the policies implemented at the government level, which it uses to estimate the time-varying parameters of an SIR model for forecasting the number of new infections 1- to 4-weeks in advance.It also forecasts the probability of changes in those government policies at each of these future times, which is essential for the longer-range forecasts. We applied SIMLR to data from regions in Canada and in the United States,and show that its MAPE (mean average percentage error) performance is as good as SOTA forecasting models, with the added advantage of being an interpretable model. We expect that this approach will be useful not only for forecasting COVID-19 infections, but also in predicting the evolution of other infectious diseases.

Sample Efficient Learning of Image-Based Diagnostic Classifiers Using Probabilistic Labels

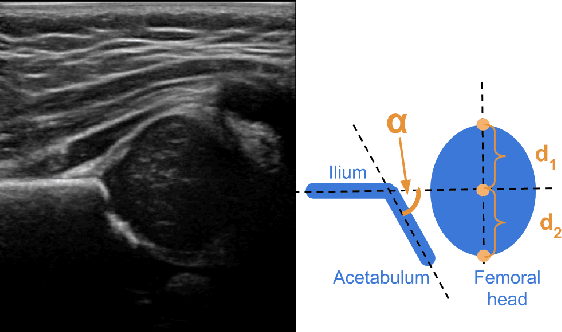
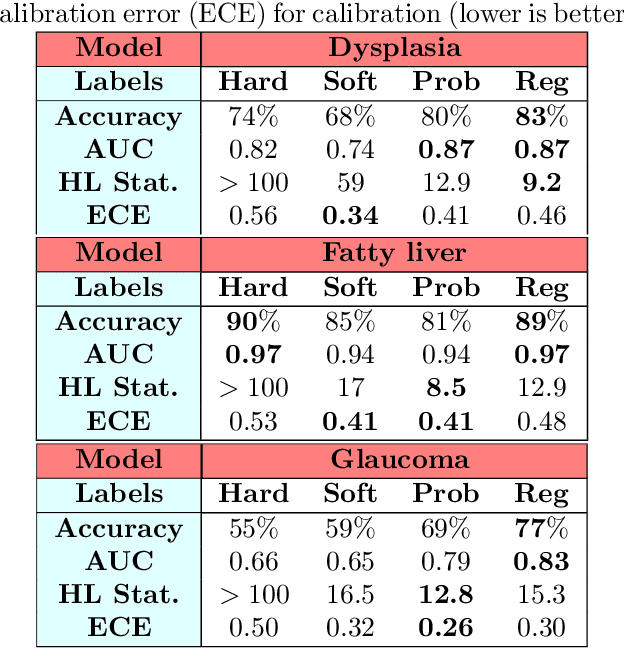
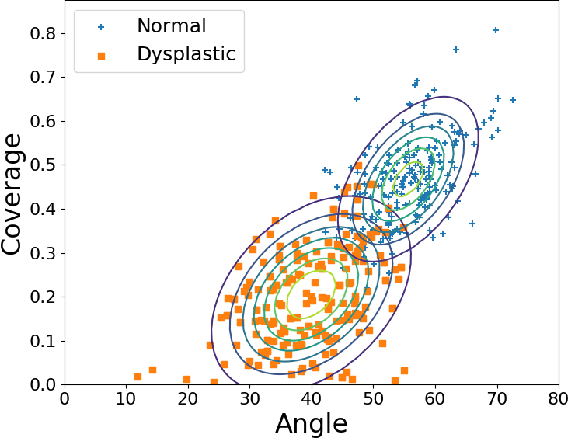
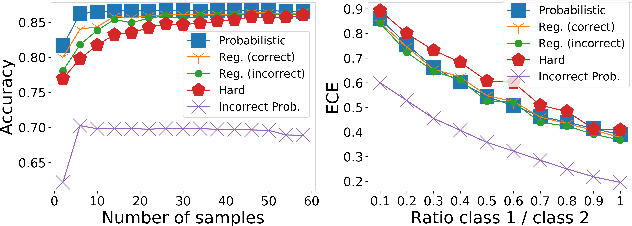
Deep learning approaches often require huge datasets to achieve good generalization. This complicates its use in tasks like image-based medical diagnosis, where the small training datasets are usually insufficient to learn appropriate data representations. For such sensitive tasks it is also important to provide the confidence in the predictions. Here, we propose a way to learn and use probabilistic labels to train accurate and calibrated deep networks from relatively small datasets. We observe gains of up to 22% in the accuracy of models trained with these labels, as compared with traditional approaches, in three classification tasks: diagnosis of hip dysplasia, fatty liver, and glaucoma. The outputs of models trained with probabilistic labels are calibrated, allowing the interpretation of its predictions as proper probabilities. We anticipate this approach will apply to other tasks where few training instances are available and expert knowledge can be encoded as probabilities.