Better-than-KL PAC-Bayes Bounds

Let $f(\theta, X_1),$ $ \dots,$ $ f(\theta, X_n)$ be a sequence of random elements, where $f$ is a fixed scalar function, $X_1, \dots, X_n$ are independent random variables (data), and $\theta$ is a random parameter distributed according to some data-dependent posterior distribution $P_n$. In this paper, we consider the problem of proving concentration inequalities to estimate the mean of the sequence. An example of such a problem is the estimation of the generalization error of some predictor trained by a stochastic algorithm, such as a neural network where $f$ is a loss function. Classically, this problem is approached through a PAC-Bayes analysis where, in addition to the posterior, we choose a prior distribution which captures our belief about the inductive bias of the learning problem. Then, the key quantity in PAC-Bayes concentration bounds is a divergence that captures the complexity of the learning problem where the de facto standard choice is the KL divergence. However, the tightness of this choice has rarely been questioned. In this paper, we challenge the tightness of the KL-divergence-based bounds by showing that it is possible to achieve a strictly tighter bound. In particular, we demonstrate new high-probability PAC-Bayes bounds with a novel and better-than-KL divergence that is inspired by Zhang et al. (2022). Our proof is inspired by recent advances in regret analysis of gambling algorithms, and its use to derive concentration inequalities. Our result is first-of-its-kind in that existing PAC-Bayes bounds with non-KL divergences are not known to be strictly better than KL. Thus, we believe our work marks the first step towards identifying optimal rates of PAC-Bayes bounds.

Mixture Weight Estimation and Model Prediction in Multi-source Multi-target Domain Adaptation

We consider the problem of learning a model from multiple heterogeneous sources with the goal of performing well on a new target distribution. The goal of learner is to mix these data sources in a target-distribution aware way and simultaneously minimize the empirical risk on the mixed source. The literature has made some tangible advancements in establishing theory of learning on mixture domain. However, there are still two unsolved problems. Firstly, how to estimate the optimal mixture of sources, given a target domain; Secondly, when there are numerous target domains, how to solve empirical risk minimization (ERM) for each target using possibly unique mixture of data sources in a computationally efficient manner. In this paper we address both problems efficiently and with guarantees. We cast the first problem, mixture weight estimation, as a convex-nonconcave compositional minimax problem, and propose an efficient stochastic algorithm with provable stationarity guarantees. Next, for the second problem, we identify that for certain regimes, solving ERM for each target domain individually can be avoided, and instead parameters for a target optimal model can be viewed as a non-linear function on a space of the mixture coefficients. Building upon this, we show that in the offline setting, a GD-trained overparameterized neural network can provably learn such function to predict the model of target domain instead of solving a designated ERM problem. Finally, we also consider an online setting and propose a label efficient online algorithm, which predicts parameters for new targets given an arbitrary sequence of mixing coefficients, while enjoying regret guarantees.

Tighter PAC-Bayes Bounds Through Coin-Betting

We consider the problem of estimating the mean of a sequence of random elements $f(X_1, \theta)$ $, \ldots, $ $f(X_n, \theta)$ where $f$ is a fixed scalar function, $S=(X_1, \ldots, X_n)$ are independent random variables, and $\theta$ is a possibly $S$-dependent parameter. An example of such a problem would be to estimate the generalization error of a neural network trained on $n$ examples where $f$ is a loss function. Classically, this problem is approached through concentration inequalities holding uniformly over compact parameter sets of functions $f$, for example as in Rademacher or VC type analysis. However, in many problems, such inequalities often yield numerically vacuous estimates. Recently, the \emph{PAC-Bayes} framework has been proposed as a better alternative for this class of problems for its ability to often give numerically non-vacuous bounds. In this paper, we show that we can do even better: we show how to refine the proof strategy of the PAC-Bayes bounds and achieve \emph{even tighter} guarantees. Our approach is based on the \emph{coin-betting} framework that derives the numerically tightest known time-uniform concentration inequalities from the regret guarantees of online gambling algorithms. In particular, we derive the first PAC-Bayes concentration inequality based on the coin-betting approach that holds simultaneously for all sample sizes. We demonstrate its tightness showing that by \emph{relaxing} it we obtain a number of previous results in a closed form including Bernoulli-KL and empirical Bernstein inequalities. Finally, we propose an efficient algorithm to numerically calculate confidence sequences from our bound, which often generates nonvacuous confidence bounds even with one sample, unlike the state-of-the-art PAC-Bayes bounds.

Learning Lipschitz Functions by GD-trained Shallow Overparameterized ReLU Neural Networks

We explore the ability of overparameterized shallow ReLU neural networks to learn Lipschitz, non-differentiable, bounded functions with additive noise when trained by Gradient Descent (GD). To avoid the problem that in the presence of noise, neural networks trained to nearly zero training error are inconsistent in this class, we focus on the early-stopped GD which allows us to show consistency and optimal rates. In particular, we explore this problem from the viewpoint of the Neural Tangent Kernel (NTK) approximation of a GD-trained finite-width neural network. We show that whenever some early stopping rule is guaranteed to give an optimal rate (of excess risk) on the Hilbert space of the kernel induced by the ReLU activation function, the same rule can be used to achieve minimax optimal rate for learning on the class of considered Lipschitz functions by neural networks. We discuss several data-free and data-dependent practically appealing stopping rules that yield optimal rates.

Stability & Generalisation of Gradient Descent for Shallow Neural Networks without the Neural Tangent Kernel

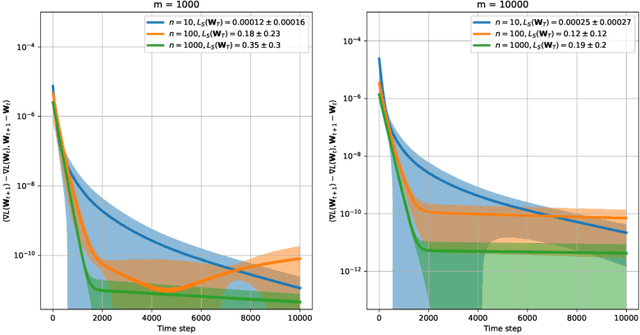
We revisit on-average algorithmic stability of Gradient Descent (GD) for training overparameterised shallow neural networks and prove new generalisation and excess risk bounds without the Neural Tangent Kernel (NTK) or Polyak-{\L}ojasiewicz (PL) assumptions. In particular, we show oracle type bounds which reveal that the generalisation and excess risk of GD is controlled by an interpolating network with the shortest GD path from initialisation (in a sense, an interpolating network with the smallest relative norm). While this was known for kernelised interpolants, our proof applies directly to networks trained by GD without intermediate kernelisation. At the same time, by relaxing oracle inequalities developed here we recover existing NTK-based risk bounds in a straightforward way, which demonstrates that our analysis is tighter. Finally, unlike most of the NTK-based analyses we focus on regression with label noise and show that GD with early stopping is consistent.

On the Role of Optimization in Double Descent: A Least Squares Study

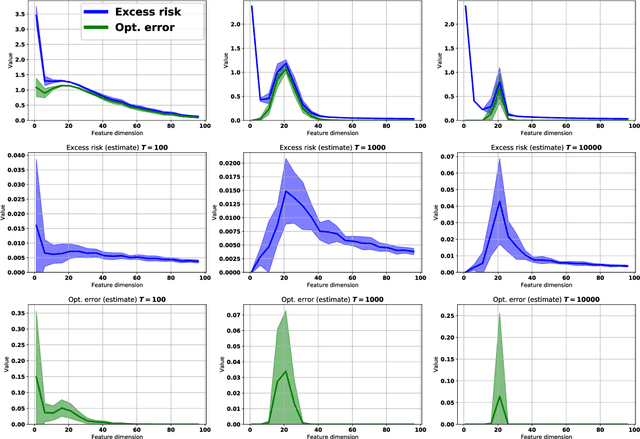
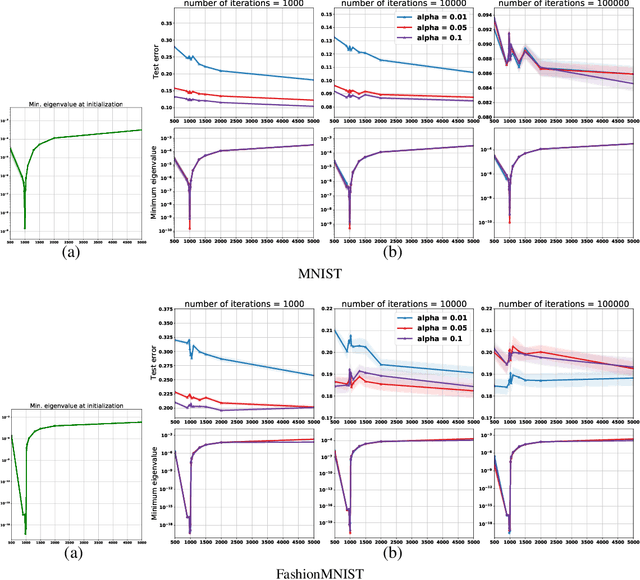
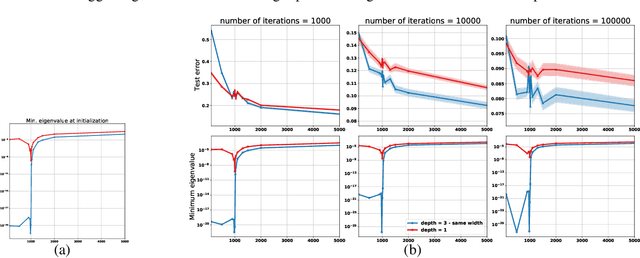
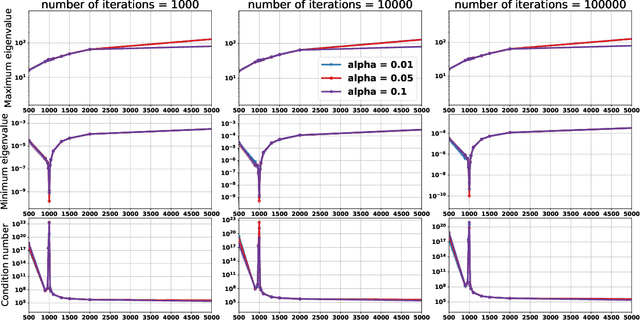
Empirically it has been observed that the performance of deep neural networks steadily improves as we increase model size, contradicting the classical view on overfitting and generalization. Recently, the double descent phenomena has been proposed to reconcile this observation with theory, suggesting that the test error has a second descent when the model becomes sufficiently overparameterized, as the model size itself acts as an implicit regularizer. In this paper we add to the growing body of work in this space, providing a careful study of learning dynamics as a function of model size for the least squares scenario. We show an excess risk bound for the gradient descent solution of the least squares objective. The bound depends on the smallest non-zero eigenvalue of the covariance matrix of the input features, via a functional form that has the double descent behavior. This gives a new perspective on the double descent curves reported in the literature. Our analysis of the excess risk allows to decouple the effect of optimization and generalization error. In particular, we find that in case of noiseless regression, double descent is explained solely by optimization-related quantities, which was missed in studies focusing on the Moore-Penrose pseudoinverse solution. We believe that our derivation provides an alternative view compared to existing work, shedding some light on a possible cause of this phenomena, at least in the considered least squares setting. We empirically explore if our predictions hold for neural networks, in particular whether the covariance of intermediary hidden activations has a similar behavior as the one predicted by our derivations.

Nonparametric Regression with Shallow Overparameterized Neural Networks Trained by GD with Early Stopping

We explore the ability of overparameterized shallow neural networks to learn Lipschitz regression functions with and without label noise when trained by Gradient Descent (GD). To avoid the problem that in the presence of noisy labels, neural networks trained to nearly zero training error are inconsistent on this class, we propose an early stopping rule that allows us to show optimal rates. This provides an alternative to the result of Hu et al. (2021) who studied the performance of $\ell 2$ -regularized GD for training shallow networks in nonparametric regression which fully relied on the infinite-width network (Neural Tangent Kernel (NTK)) approximation. Here we present a simpler analysis which is based on a partitioning argument of the input space (as in the case of 1-nearest-neighbor rule) coupled with the fact that trained neural networks are smooth with respect to their inputs when trained by GD. In the noise-free case the proof does not rely on any kernelization and can be regarded as a finite-width result. In the case of label noise, by slightly modifying the proof, the noise is controlled using a technique of Yao, Rosasco, and Caponnetto (2007).

On Optimality of Meta-Learning in Fixed-Design Regression with Weighted Biased Regularization

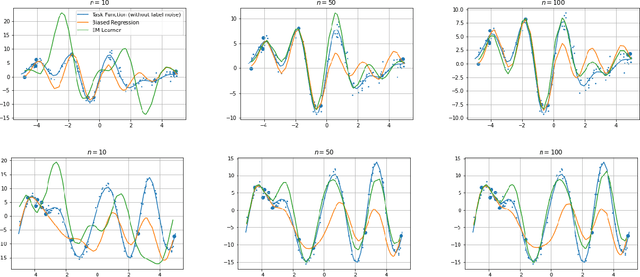
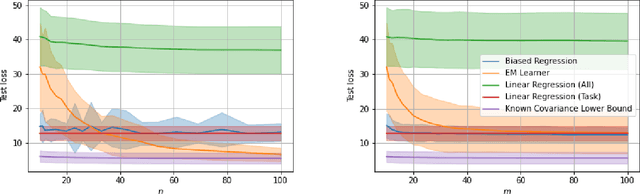
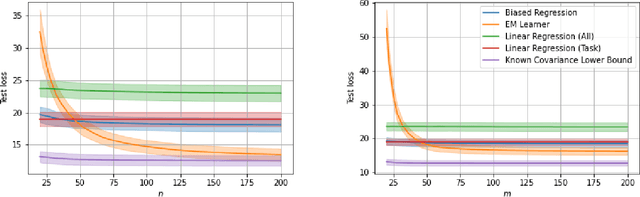
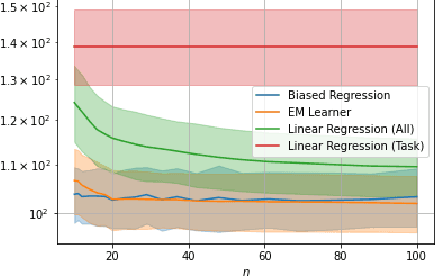
We consider a fixed-design linear regression in the meta-learning model of Baxter (2000) and establish a problem-dependent finite-sample lower bound on the transfer risk (risk on a newly observed task) valid for all estimators. Moreover, we prove that a weighted form of a biased regularization - a popular technique in transfer and meta-learning - is optimal, i.e. it enjoys a problem-dependent upper bound on the risk matching our lower bound up to a constant. Thus, our bounds characterize meta-learning linear regression problems and reveal a fine-grained dependency on the task structure. Our characterization suggests that in the non-asymptotic regime, for a sufficiently large number of tasks, meta-learning can be considerably superior to a single-task learning. Finally, we propose a practical adaptation of the optimal estimator through Expectation-Maximization procedure and show its effectiveness in series of experiments.

PAC-Bayes Analysis Beyond the Usual Bounds

We focus on a stochastic learning model where the learner observes a finite set of training examples and the output of the learning process is a data-dependent distribution over a space of hypotheses. The learned data-dependent distribution is then used to make randomized predictions, and the high-level theme addressed here is guaranteeing the quality of predictions on examples that were not seen during training, i.e. generalization. In this setting the unknown quantity of interest is the expected risk of the data-dependent randomized predictor, for which upper bounds can be derived via a PAC-Bayes analysis, leading to PAC-Bayes bounds. Specifically, we present a basic PAC-Bayes inequality for stochastic kernels, from which one may derive extensions of various known PAC-Bayes bounds as well as novel bounds. We clarify the role of the requirement of fixed `data-free' priors and illustrate the use of data-dependent priors. We also present a simple bound that is valid for a loss function with unbounded range. Our analysis clarifies that those two requirements were used to upper-bound an exponential moment term, while the basic PAC-Bayes inequality remains valid with those restrictions removed.

Confident Off-Policy Evaluation and Selection through Self-Normalized Importance Weighting

We consider off-policy evaluation in the contextual bandit setting for the purpose of obtaining a robust off-policy selection strategy, where the selection strategy is evaluated based on the value of the chosen policy in a set of proposal (target) policies. We propose a new method to compute a lower bound on the value of an arbitrary target policy given some logged data in contextual bandits for a desired coverage. The lower bound is built around the so-called Self-normalized Importance Weighting (SN) estimator. It combines the use of a semi-empirical Efron-Stein tail inequality to control the concentration and Harris' inequality to control the bias. The new approach is evaluated on a number of synthetic and real datasets and is found to be superior to its main competitors, both in terms of tightness of the confidence intervals and the quality of the policies chosen.