Almost Linear Convergence under Minimal Score Assumptions: Quantized Transition Diffusion

Continuous diffusion models have demonstrated remarkable performance in data generation across various domains, yet their efficiency remains constrained by two critical limitations: (1) the local adjacency structure of the forward Markov process, which restricts long-range transitions in the data space, and (2) inherent biases introduced during the simulation of time-inhomogeneous reverse denoising processes. To address these challenges, we propose Quantized Transition Diffusion (QTD), a novel approach that integrates data quantization with discrete diffusion dynamics. Our method first transforms the continuous data distribution $p_*$ into a discrete one $q_*$ via histogram approximation and binary encoding, enabling efficient representation in a structured discrete latent space. We then design a continuous-time Markov chain (CTMC) with Hamming distance-based transitions as the forward process, which inherently supports long-range movements in the original data space. For reverse-time sampling, we introduce a \textit{truncated uniformization} technique to simulate the reverse CTMC, which can provably provide unbiased generation from $q_*$ under minimal score assumptions. Through a novel KL dynamic analysis of the reverse CTMC, we prove that QTD can generate samples with $O(d\ln^2(d/\epsilon))$ score evaluations in expectation to approximate the $d$--dimensional target distribution $p_*$ within an $\epsilon$ error tolerance. Our method not only establishes state-of-the-art inference efficiency but also advances the theoretical foundations of diffusion-based generative modeling by unifying discrete and continuous diffusion paradigms.

Log-concave Sampling over a Convex Body with a Barrier: a Robust and Unified Dikin Walk

We consider the problem of sampling from a $d$-dimensional log-concave distribution $\pi(\theta) \propto \exp(-f(\theta))$ for $L$-Lipschitz $f$, constrained to a convex body with an efficiently computable self-concordant barrier function, contained in a ball of radius $R$ with a $w$-warm start. We propose a \emph{robust} sampling framework that computes spectral approximations to the Hessian of the barrier functions in each iteration. We prove that for polytopes that are described by $n$ hyperplanes, sampling with the Lee-Sidford barrier function mixes within $\widetilde O((d^2+dL^2R^2)\log(w/\delta))$ steps with a per step cost of $\widetilde O(nd^{\omega-1})$, where $\omega\approx 2.37$ is the fast matrix multiplication exponent. Compared to the prior work of Mangoubi and Vishnoi, our approach gives faster mixing time as we are able to design a generalized soft-threshold Dikin walk beyond log-barrier. We further extend our result to show how to sample from a $d$-dimensional spectrahedron, the constrained set of a semidefinite program, specified by the set $\{x\in \mathbb{R}^d: \sum_{i=1}^d x_i A_i \succeq C \}$ where $A_1,\ldots,A_d, C$ are $n\times n$ real symmetric matrices. We design a walk that mixes in $\widetilde O((nd+dL^2R^2)\log(w/\delta))$ steps with a per iteration cost of $\widetilde O(n^\omega+n^2d^{3\omega-5})$. We improve the mixing time bound of prior best Dikin walk due to Narayanan and Rakhlin that mixes in $\widetilde O((n^2d^3+n^2dL^2R^2)\log(w/\delta))$ steps.

Diff-BBO: Diffusion-Based Inverse Modeling for Black-Box Optimization

Black-box optimization (BBO) aims to optimize an objective function by iteratively querying a black-box oracle. This process demands sample-efficient optimization due to the high computational cost of function evaluations. While prior studies focus on forward approaches to learn surrogates for the unknown objective function, they struggle with high-dimensional inputs where valid inputs form a small subspace (e.g., valid protein sequences), which is common in real-world tasks. Recently, diffusion models have demonstrated impressive capability in learning the high-dimensional data manifold. They have shown promising performance in black-box optimization tasks but only in offline settings. In this work, we propose diffusion-based inverse modeling for black-box optimization (Diff-BBO), the first inverse approach leveraging diffusion models for online BBO problem. Diff-BBO distinguishes itself from forward approaches through the design of acquisition function. Instead of proposing candidates in the design space, Diff-BBO employs a novel acquisition function Uncertainty-aware Exploration (UaE) to propose objective function values, which leverages the uncertainty of a conditional diffusion model to generate samples in the design space. Theoretically, we prove that using UaE leads to optimal optimization outcomes. Empirically, we redesign experiments on the Design-Bench benchmark for online settings and show that Diff-BBO achieves state-of-the-art performance.

Posterior Sampling with Delayed Feedback for Reinforcement Learning with Linear Function Approximation

Recent studies in reinforcement learning (RL) have made significant progress by leveraging function approximation to alleviate the sample complexity hurdle for better performance. Despite the success, existing provably efficient algorithms typically rely on the accessibility of immediate feedback upon taking actions. The failure to account for the impact of delay in observations can significantly degrade the performance of real-world systems due to the regret blow-up. In this work, we tackle the challenge of delayed feedback in RL with linear function approximation by employing posterior sampling, which has been shown to empirically outperform the popular UCB algorithms in a wide range of regimes. We first introduce Delayed-PSVI, an optimistic value-based algorithm that effectively explores the value function space via noise perturbation with posterior sampling. We provide the first analysis for posterior sampling algorithms with delayed feedback in RL and show our algorithm achieves $\widetilde{O}(\sqrt{d^3H^3 T} + d^2H^2 E[\tau])$ worst-case regret in the presence of unknown stochastic delays. Here $E[\tau]$ is the expected delay. To further improve its computational efficiency and to expand its applicability in high-dimensional RL problems, we incorporate a gradient-based approximate sampling scheme via Langevin dynamics for Delayed-LPSVI, which maintains the same order-optimal regret guarantee with $\widetilde{O}(dHK)$ computational cost. Empirical evaluations are performed to demonstrate the statistical and computational efficacy of our algorithms.

Langevin Thompson Sampling with Logarithmic Communication: Bandits and Reinforcement Learning

Thompson sampling (TS) is widely used in sequential decision making due to its ease of use and appealing empirical performance. However, many existing analytical and empirical results for TS rely on restrictive assumptions on reward distributions, such as belonging to conjugate families, which limits their applicability in realistic scenarios. Moreover, sequential decision making problems are often carried out in a batched manner, either due to the inherent nature of the problem or to serve the purpose of reducing communication and computation costs. In this work, we jointly study these problems in two popular settings, namely, stochastic multi-armed bandits (MABs) and infinite-horizon reinforcement learning (RL), where TS is used to learn the unknown reward distributions and transition dynamics, respectively. We propose batched $\textit{Langevin Thompson Sampling}$ algorithms that leverage MCMC methods to sample from approximate posteriors with only logarithmic communication costs in terms of batches. Our algorithms are computationally efficient and maintain the same order-optimal regret guarantees of $\mathcal{O}(\log T)$ for stochastic MABs, and $\mathcal{O}(\sqrt{T})$ for RL. We complement our theoretical findings with experimental results.

Statistical and Computational Trade-offs in Variational Inference: A Case Study in Inferential Model Selection

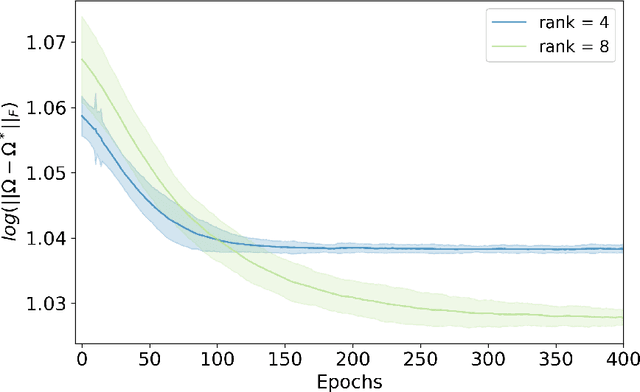
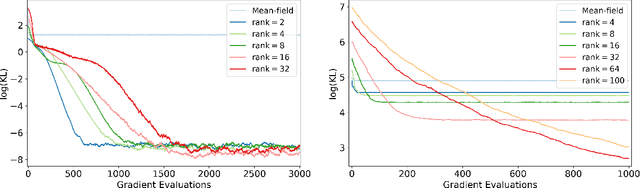
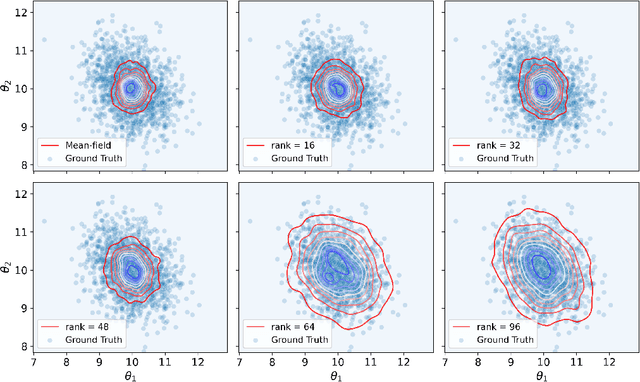
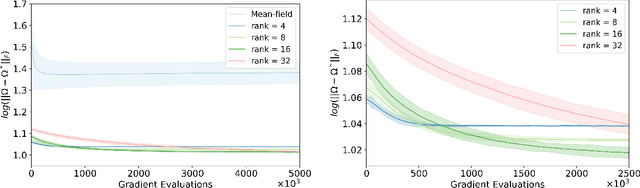
Variational inference has recently emerged as a popular alternative to the classical Markov chain Monte Carlo (MCMC) in large-scale Bayesian inference. The core idea of variational inference is to trade statistical accuracy for computational efficiency. It aims to approximate the posterior, reducing computation costs but potentially compromising its statistical accuracy. In this work, we study this statistical and computational trade-off in variational inference via a case study in inferential model selection. Focusing on Gaussian inferential models (a.k.a. variational approximating families) with diagonal plus low-rank precision matrices, we initiate a theoretical study of the trade-offs in two aspects, Bayesian posterior inference error and frequentist uncertainty quantification error. From the Bayesian posterior inference perspective, we characterize the error of the variational posterior relative to the exact posterior. We prove that, given a fixed computation budget, a lower-rank inferential model produces variational posteriors with a higher statistical approximation error, but a lower computational error; it reduces variances in stochastic optimization and, in turn, accelerates convergence. From the frequentist uncertainty quantification perspective, we consider the precision matrix of the variational posterior as an uncertainty estimate. We find that, relative to the true asymptotic precision, the variational approximation suffers from an additional statistical error originating from the sampling uncertainty of the data. Moreover, this statistical error becomes the dominant factor as the computation budget increases. As a consequence, for small datasets, the inferential model need not be full-rank to achieve optimal estimation error. We finally demonstrate these statistical and computational trade-offs inference across empirical studies, corroborating the theoretical findings.

Performance Effectiveness of Multimedia Information Search Using the Epsilon-Greedy Algorithm

In the search and retrieval of multimedia objects, it is impractical to either manually or automatically extract the contents for indexing since most of the multimedia contents are not machine extractable, while manual extraction tends to be highly laborious and time-consuming. However, by systematically capturing and analyzing the feedback patterns of human users, vital information concerning the multimedia contents can be harvested for effective indexing and subsequent search. By learning from the human judgment and mental evaluation of users, effective search indices can be gradually developed and built up, and subsequently be exploited to find the most relevant multimedia objects. To avoid hovering around a local maximum, we apply the epsilon-greedy method to systematically explore the search space. Through such methodic exploration, we show that the proposed approach is able to guarantee that the most relevant objects can always be discovered, even though initially it may have been overlooked or not regarded as relevant. The search behavior of the present approach is quantitatively analyzed, and closed-form expressions are obtained for the performance of two variants of the epsilon-greedy algorithm, namely EGSE-A and EGSE-B. Simulations and experiments on real data set have been performed which show good agreement with the theoretical findings. The present method is able to leverage exploration in an effective way to significantly raise the performance of multimedia information search, and enables the certain discovery of relevant objects which may be otherwise undiscoverable.

Analysis of Evolutionary Behavior in Self-Learning Media Search Engines

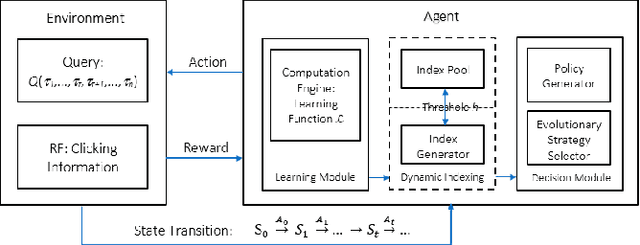
The diversity of intrinsic qualities of multimedia entities tends to impede their effective retrieval. In a SelfLearning Search Engine architecture, the subtle nuances of human perceptions and deep knowledge are taught and captured through unsupervised reinforcement learning, where the degree of reinforcement may be suitably calibrated. Such architectural paradigm enables indexes to evolve naturally while accommodating the dynamic changes of user interests. It operates by continuously constructing indexes over time, while injecting progressive improvement in search performance. For search operations to be effective, convergence of index learning is of crucial importance to ensure efficiency and robustness. In this paper, we develop a Self-Learning Search Engine architecture based on reinforcement learning using a Markov Decision Process framework. The balance between exploration and exploitation is achieved through evolutionary exploration Strategies. The evolutionary index learning behavior is then studied and formulated using stochastic analysis. Experimental results are presented which corroborate the steady convergence of the index evolution mechanism. Index Term

Leveraging Reinforcement Learning Techniques for Effective Policy Adoption and Validation

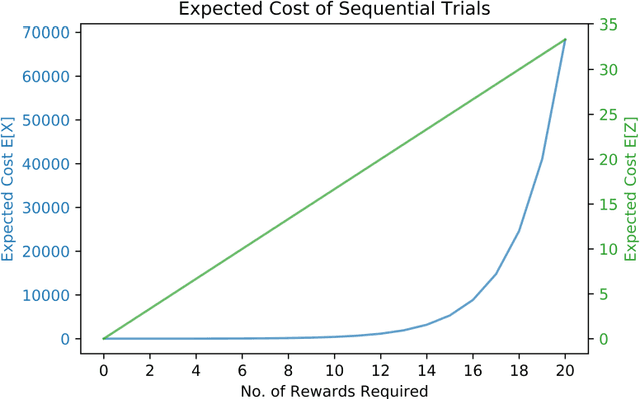
Rewards and punishments in different forms are pervasive and present in a wide variety of decision-making scenarios. By observing the outcome of a sufficient number of repeated trials, one would gradually learn the value and usefulness of a particular policy or strategy. However, in a given environment, the outcomes resulting from different trials are subject to chance influence and variations. In learning about the usefulness of a given policy, significant costs are involved in systematically undertaking the sequential trials; therefore, in most learning episodes, one would wish to keep the cost within bounds by adopting learning stopping rules. In this paper, we examine the deployment of different stopping strategies in given learning environments which vary from highly stringent for mission critical operations to highly tolerant for non-mission critical operations, and emphasis is placed on the former with particular application to aviation safety. In policy evaluation, two sequential phases of learning are identified, and we describe the outcomes variations using a probabilistic model, with closedform expressions obtained for the key measures of performance. Decision rules that map the trial observations to policy choices are also formulated. In addition, simulation experiments are performed, which corroborate the validity of the theoretical results.

Performance Dynamics and Termination Errors in Reinforcement Learning: A Unifying Perspective

In reinforcement learning, a decision needs to be made at some point as to whether it is worthwhile to carry on with the learning process or to terminate it. In many such situations, stochastic elements are often present which govern the occurrence of rewards, with the sequential occurrences of positive rewards randomly interleaved with negative rewards. For most practical learners, the learning is considered useful if the number of positive rewards always exceeds the negative ones. A situation that often calls for learning termination is when the number of negative rewards exceeds the number of positive rewards. However, while this seems reasonable, the error of premature termination, whereby termination is enacted along with the conclusion of learning failure despite the positive rewards eventually far outnumber the negative ones, can be significant. In this paper, using combinatorial analysis we study the error probability in wrongly terminating a reinforcement learning activity which undermines the effectiveness of an optimal policy, and we show that the resultant error can be quite high. Whilst we demonstrate mathematically that such errors can never be eliminated, we propose some practical mechanisms that can effectively reduce such errors. Simulation experiments have been carried out, the results of which are in close agreement with our theoretical findings.