Dual Low-Rank Adaptation for Continual Learning with Pre-Trained Models

In the era of foundation models, we revisit continual learning~(CL), which aims to enable vision transformers (ViTs) to learn new tasks over time. However, as the scale of these models increases, catastrophic forgetting remains a persistent challenge, particularly in the presence of significant domain shifts across tasks. Recent studies highlight a crossover between CL techniques and parameter-efficient fine-tuning (PEFT), which focuses on fine-tuning only a small set of trainable parameters to adapt to downstream tasks, such as low-rank adaptation (LoRA). While LoRA achieves faster convergence and requires fewer trainable parameters, it has seldom been explored in the context of continual learning. To address this gap, we propose a novel PEFT-CL method called Dual Low-Rank Adaptation (DualLoRA), which introduces both an orthogonal LoRA adapter and a residual LoRA adapter parallel to pre-trained weights in each layer. These components are orchestrated by a dynamic memory mechanism to strike a balance between stability and plasticity. The orthogonal LoRA adapter's parameters are updated in an orthogonal subspace of previous tasks to mitigate catastrophic forgetting, while the residual LoRA adapter's parameters are updated in the residual subspace spanned by task-specific bases without interaction across tasks, offering complementary capabilities for fine-tuning new tasks. On ViT-based models, we demonstrate that DualLoRA offers significant advantages in accuracy, inference speed, and memory efficiency over existing CL methods across multiple benchmarks.

FedP3: Federated Personalized and Privacy-friendly Network Pruning under Model Heterogeneity

The interest in federated learning has surged in recent research due to its unique ability to train a global model using privacy-secured information held locally on each client. This paper pays particular attention to the issue of client-side model heterogeneity, a pervasive challenge in the practical implementation of FL that escalates its complexity. Assuming a scenario where each client possesses varied memory storage, processing capabilities and network bandwidth - a phenomenon referred to as system heterogeneity - there is a pressing need to customize a unique model for each client. In response to this, we present an effective and adaptable federated framework FedP3, representing Federated Personalized and Privacy-friendly network Pruning, tailored for model heterogeneity scenarios. Our proposed methodology can incorporate and adapt well-established techniques to its specific instances. We offer a theoretical interpretation of FedP3 and its locally differential-private variant, DP-FedP3, and theoretically validate their efficiencies.

Privacy Assessment on Reconstructed Images: Are Existing Evaluation Metrics Faithful to Human Perception?

Hand-crafted image quality metrics, such as PSNR and SSIM, are commonly used to evaluate model privacy risk under reconstruction attacks. Under these metrics, reconstructed images that are determined to resemble the original one generally indicate more privacy leakage. Images determined as overall dissimilar, on the other hand, indicate higher robustness against attack. However, there is no guarantee that these metrics well reflect human opinions, which, as a judgement for model privacy leakage, are more trustworthy. In this paper, we comprehensively study the faithfulness of these hand-crafted metrics to human perception of privacy information from the reconstructed images. On 5 datasets ranging from natural images, faces, to fine-grained classes, we use 4 existing attack methods to reconstruct images from many different classification models and, for each reconstructed image, we ask multiple human annotators to assess whether this image is recognizable. Our studies reveal that the hand-crafted metrics only have a weak correlation with the human evaluation of privacy leakage and that even these metrics themselves often contradict each other. These observations suggest risks of current metrics in the community. To address this potential risk, we propose a learning-based measure called SemSim to evaluate the Semantic Similarity between the original and reconstructed images. SemSim is trained with a standard triplet loss, using an original image as an anchor, one of its recognizable reconstructed images as a positive sample, and an unrecognizable one as a negative. By training on human annotations, SemSim exhibits a greater reflection of privacy leakage on the semantic level. We show that SemSim has a significantly higher correlation with human judgment compared with existing metrics. Moreover, this strong correlation generalizes to unseen datasets, models and attack methods.

On the Hardness of Robustness Transfer: A Perspective from Rademacher Complexity over Symmetric Difference Hypothesis Space

Recent studies demonstrated that the adversarially robust learning under $\ell_\infty$ attack is harder to generalize to different domains than standard domain adaptation. How to transfer robustness across different domains has been a key question in domain adaptation field. To investigate the fundamental difficulty behind adversarially robust domain adaptation (or robustness transfer), we propose to analyze a key complexity measure that controls the cross-domain generalization: the adversarial Rademacher complexity over {\em symmetric difference hypothesis space} $\mathcal{H} \Delta \mathcal{H}$. For linear models, we show that adversarial version of this complexity is always greater than the non-adversarial one, which reveals the intrinsic hardness of adversarially robust domain adaptation. We also establish upper bounds on this complexity measure. Then we extend them to the ReLU neural network class by upper bounding the adversarial Rademacher complexity in the binary classification setting. Finally, even though the robust domain adaptation is provably harder, we do find positive relation between robust learning and standard domain adaptation. We explain \emph{how adversarial training helps domain adaptation in terms of standard risk}. We believe our results initiate the study of the generalization theory of adversarially robust domain adaptation, and could shed lights on distributed adversarially robust learning from heterogeneous sources, e.g., federated learning scenario.

Cutting Some Slack for SGD with Adaptive Polyak Stepsizes

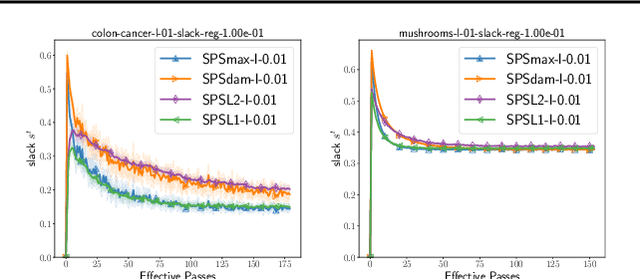
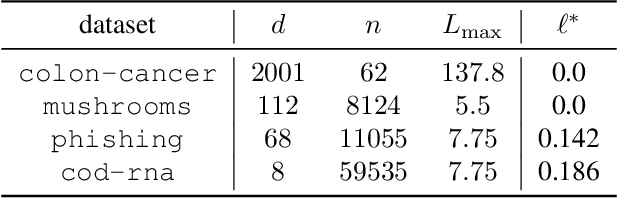
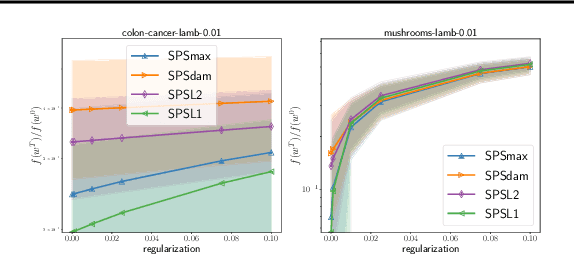
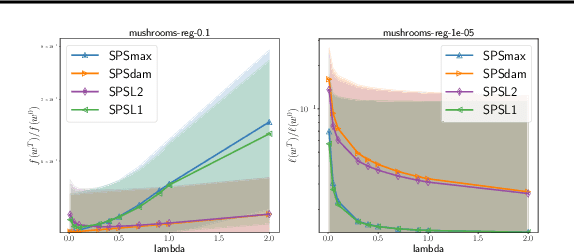
Tuning the step size of stochastic gradient descent is tedious and error prone. This has motivated the development of methods that automatically adapt the step size using readily available information. In this paper, we consider the family of SPS (Stochastic gradient with a Polyak Stepsize) adaptive methods. These are methods that make use of gradient and loss value at the sampled points to adaptively adjust the step size. We first show that SPS and its recent variants can all be seen as extensions of the Passive-Aggressive methods applied to nonlinear problems. We use this insight to develop new variants of the SPS method that are better suited to nonlinear models. Our new variants are based on introducing a slack variable into the interpolation equations. This single slack variable tracks the loss function across iterations and is used in setting a stable step size. We provide extensive numerical results supporting our new methods and a convergence theory.

Towards closing the gap between the theory and practice of SVRG

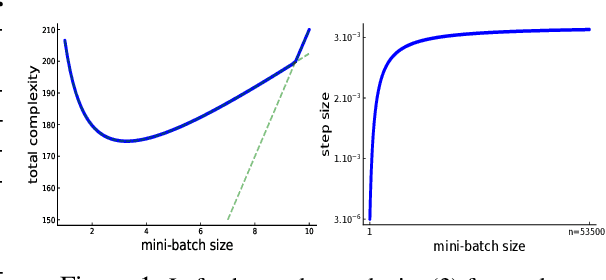
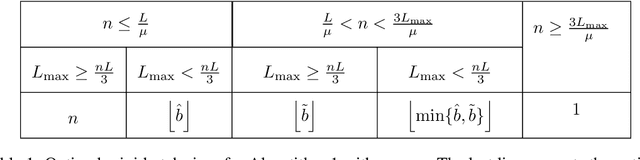
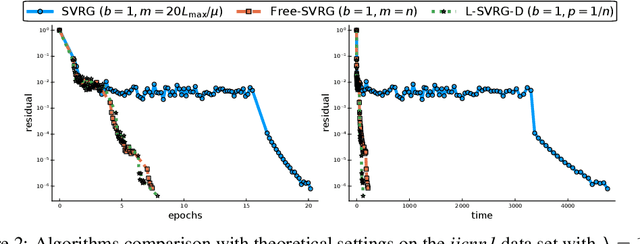
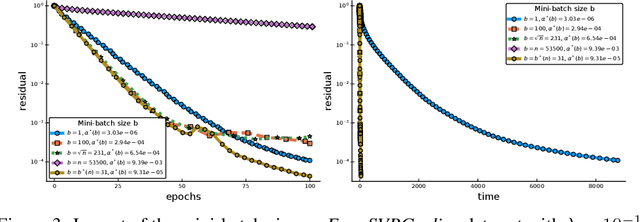
Among the very first variance reduced stochastic methods for solving the empirical risk minimization problem was the SVRG method (Johnson & Zhang 2013). SVRG is an inner-outer loop based method, where in the outer loop a reference full gradient is evaluated, after which $m \in \mathbb{N}$ steps of an inner loop are executed where the reference gradient is used to build a variance reduced estimate of the current gradient. The simplicity of the SVRG method and its analysis has lead to multiple extensions and variants for even non-convex optimization. Yet there is a significant gap between the parameter settings that the analysis suggests and what is known to work well in practice. Our first contribution is that we take several steps towards closing this gap. In particular, the current analysis shows that $m$ should be of the order of the condition number so that the resulting method has a favorable complexity. Yet in practice $m =n$ works well irregardless of the condition number, where $n$ is the number of data points. Furthermore, the current analysis shows that the inner iterates have to be reset using averaging after every outer loop. Yet in practice SVRG works best when the inner iterates are updated continuously and not reset. We provide an analysis of these aforementioned practical settings and show that they achieve the same favorable complexity as the original analysis (with slightly better constants). Our second contribution is to provide a more general analysis than had been previously done by using arbitrary sampling, which allows us to analyse virtually all forms of mini-batching through a single theorem. Since our setup and analysis reflects what is done in practice, we are able to set the parameters such as the mini-batch size and step size using our theory in such a way that produces a more efficient algorithm in practice, as we show in extensive numerical experiments.

Optimal mini-batch and step sizes for SAGA

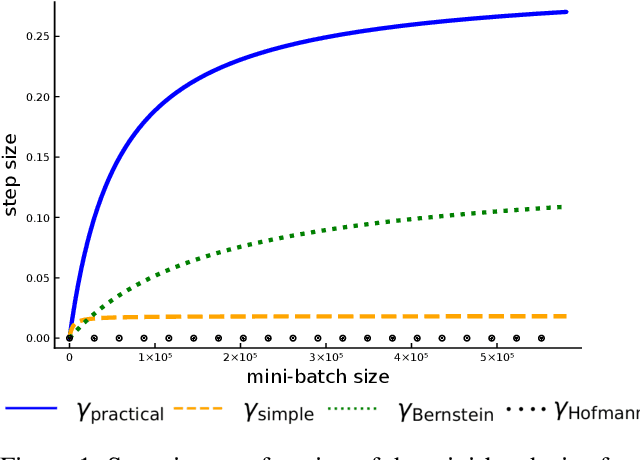
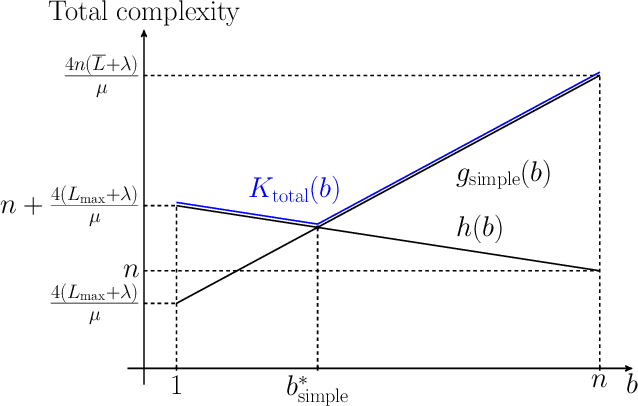
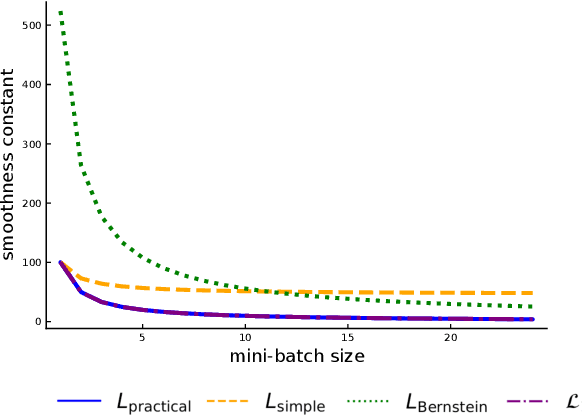
Recently it has been shown that the step sizes of a family of variance reduced gradient methods called the JacSketch methods depend on the expected smoothness constant. In particular, if this expected smoothness constant could be calculated a priori, then one could safely set much larger step sizes which would result in a much faster convergence rate. We fill in this gap, and provide simple closed form expressions for the expected smoothness constant and careful numerical experiments verifying these bounds. Using these bounds, and since the SAGA algorithm is part of this JacSketch family, we suggest a new standard practice for setting the step sizes and mini-batch size for SAGA that are competitive with a numerical grid search. Furthermore, we can now show that the total complexity of the SAGA algorithm decreases linearly in the mini-batch size up to a pre-defined value: the optimal mini-batch size. This is a rare result in the stochastic variance reduced literature, only previously shown for the Katyusha algorithm. Finally we conjecture that this is the case for many other stochastic variance reduced methods and that our bounds and analysis of the expected smoothness constant is key to extending these results.