Othmane Sebbouh
Structured Transforms Across Spaces with Cost-Regularized Optimal Transport
Nov 23, 2023



Abstract:Matching a source to a target probability measure is often solved by instantiating a linear optimal transport (OT) problem, parameterized by a ground cost function that quantifies discrepancy between points. When these measures live in the same metric space, the ground cost often defaults to its distance. When instantiated across two different spaces, however, choosing that cost in the absence of aligned data is a conundrum. As a result, practitioners often resort to solving instead a quadratic Gromow-Wasserstein (GW) problem. We exploit in this work a parallel between GW and cost-regularized OT, the regularized minimization of a linear OT objective parameterized by a ground cost. We use this cost-regularized formulation to match measures across two different Euclidean spaces, where the cost is evaluated between transformed source points and target points. We show that several quadratic OT problems fall in this category, and consider enforcing structure in linear transform (e.g. sparsity), by introducing structure-inducing regularizers. We provide a proximal algorithm to extract such transforms from unaligned data, and demonstrate its applicability to single-cell spatial transcriptomics/multiomics matching tasks.
Randomized Stochastic Gradient Descent Ascent
Nov 25, 2021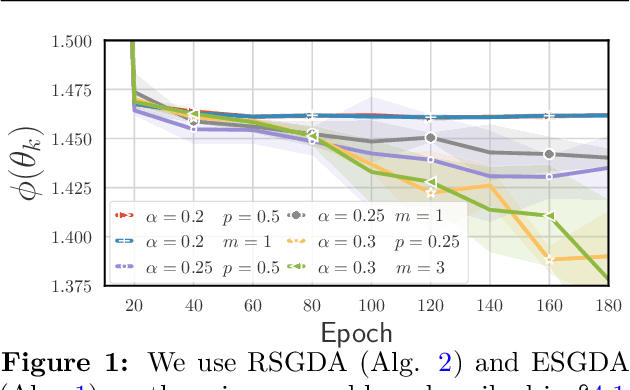
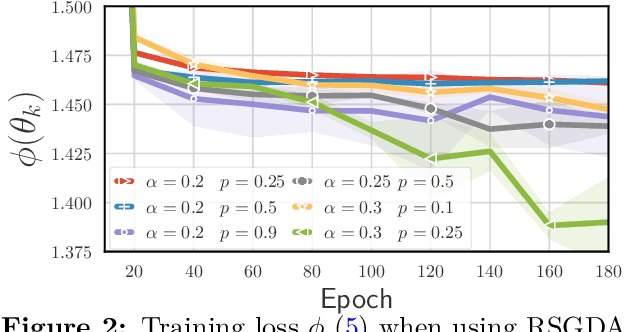
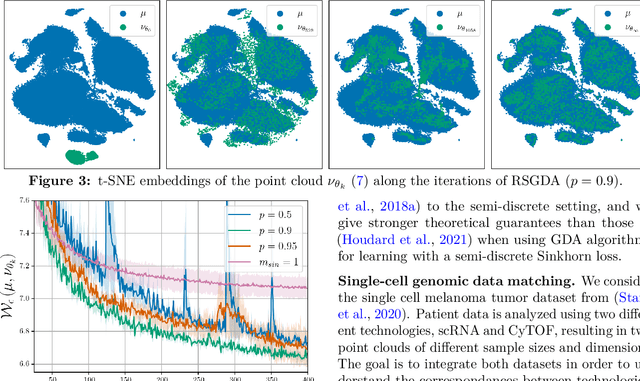
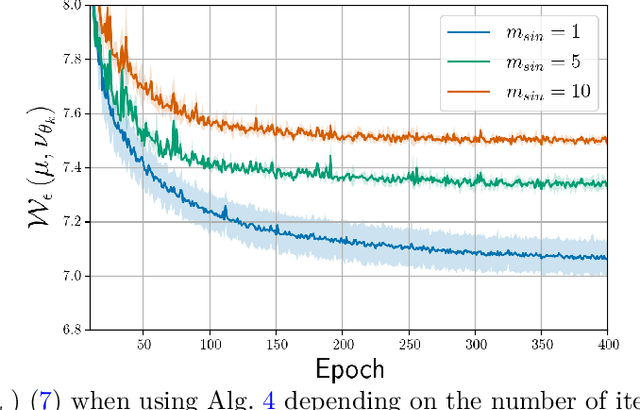
Abstract:An increasing number of machine learning problems, such as robust or adversarial variants of existing algorithms, require minimizing a loss function that is itself defined as a maximum. Carrying a loop of stochastic gradient ascent (SGA) steps on the (inner) maximization problem, followed by an SGD step on the (outer) minimization, is known as Epoch Stochastic Gradient \textit{Descent Ascent} (ESGDA). While successful in practice, the theoretical analysis of ESGDA remains challenging, with no clear guidance on choices for the inner loop size nor on the interplay between inner/outer step sizes. We propose RSGDA (Randomized SGDA), a variant of ESGDA with stochastic loop size with a simpler theoretical analysis. RSGDA comes with the first (among SGDA algorithms) almost sure convergence rates when used on nonconvex min/strongly-concave max settings. RSGDA can be parameterized using optimal loop sizes that guarantee the best convergence rates known to hold for SGDA. We test RSGDA on toy and larger scale problems, using distributionally robust optimization and single-cell data matching using optimal transport as a testbed.
Unified Analysis of Stochastic Gradient Methods for Composite Convex and Smooth Optimization
Jun 20, 2020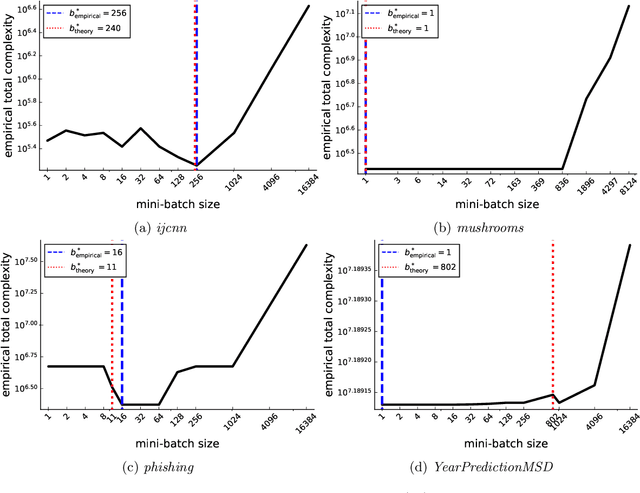
Abstract:We present a unified theorem for the convergence analysis of stochastic gradient algorithms for minimizing a smooth and convex loss plus a convex regularizer. We do this by extending the unified analysis of Gorbunov, Hanzely \& Richt\'arik (2020) and dropping the requirement that the loss function be strongly convex. Instead, we only rely on convexity of the loss function. Our unified analysis applies to a host of existing algorithms such as proximal SGD, variance reduced methods, quantization and some coordinate descent type methods. For the variance reduced methods, we recover the best known convergence rates as special cases. For proximal SGD, the quantization and coordinate type methods, we uncover new state-of-the-art convergence rates. Our analysis also includes any form of sampling and minibatching. As such, we are able to determine the minibatch size that optimizes the total complexity of variance reduced methods. We showcase this by obtaining a simple formula for the optimal minibatch size of two variance reduced methods (\textit{L-SVRG} and \textit{SAGA}). This optimal minibatch size not only improves the theoretical total complexity of the methods but also improves their convergence in practice, as we show in several experiments.
SGD for Structured Nonconvex Functions: Learning Rates, Minibatching and Interpolation
Jun 19, 2020
Abstract:We provide several convergence theorems for SGD for two large classes of structured non-convex functions: (i) the Quasar (Strongly) Convex functions and (ii) the functions satisfying the Polyak-Lojasiewicz condition. Our analysis relies on the Expected Residual condition which we show is a strictly weaker assumption as compared to previously used growth conditions, expected smoothness or bounded variance assumptions. We provide theoretical guarantees for the convergence of SGD for different step size selections including constant, decreasing and the recently proposed stochastic Polyak step size. In addition, all of our analysis holds for the arbitrary sampling paradigm, and as such, we are able to give insights into the complexity of minibatching and determine an optimal minibatch size. In particular we recover the best known convergence rates of full gradient descent and single element sampling SGD as a special case. Finally, we show that for models that interpolate the training data, we can dispense of our Expected Residual condition and give state-of-the-art results in this setting.
On the convergence of the Stochastic Heavy Ball Method
Jun 14, 2020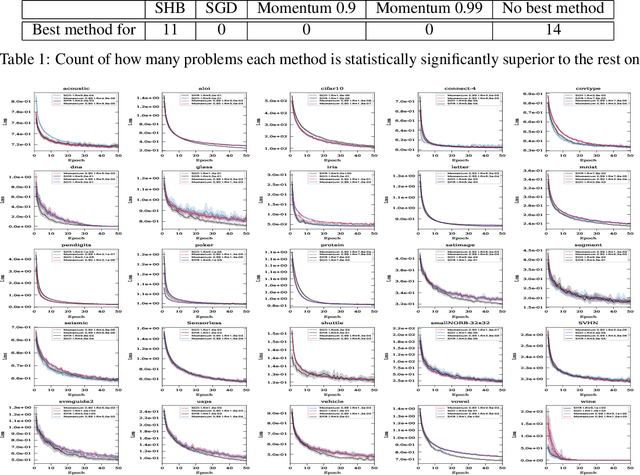
Abstract:We provide a comprehensive analysis of the Stochastic Heavy Ball (SHB) method (otherwise known as the momentum method), including a convergence of the last iterate of SHB, establishing a faster rate of convergence than existing bounds on the last iterate of Stochastic Gradient Descent (SGD) in the convex setting. Our analysis shows that unlike SGD, no final iterate averaging is necessary with the SHB method. We detail new iteration dependent step sizes (learning rates) and momentum parameters for the SHB that result in this fast convergence. Moreover, assuming only smoothness and convexity, we prove that the iterates of SHB converge \textit{almost surely} to a minimizer, and that the convergence of the function values of (S)HB is asymptotically faster than that of (S)GD in the overparametrized and in the deterministic settings. Our analysis is general, in that it includes all forms of mini-batching and non-uniform samplings as a special case, using an arbitrary sampling framework. Furthermore, our analysis does not rely on the bounded gradient assumptions. Instead, it only relies on smoothness, which is an assumption that can be more readily verified. Finally, we present extensive numerical experiments that show that our theoretically motivated parameter settings give a statistically significant faster convergence across a diverse collection of datasets.
Towards closing the gap between the theory and practice of SVRG
Jul 31, 2019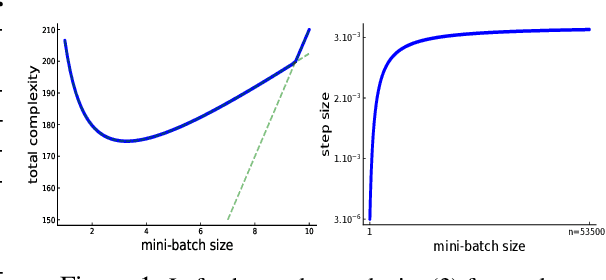
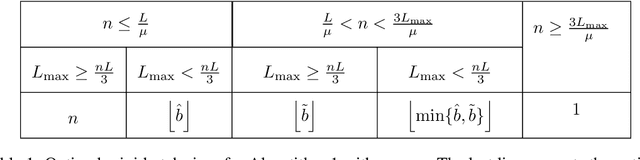
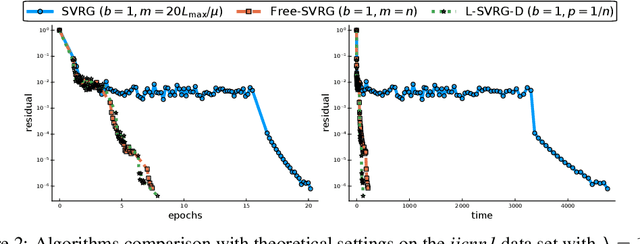
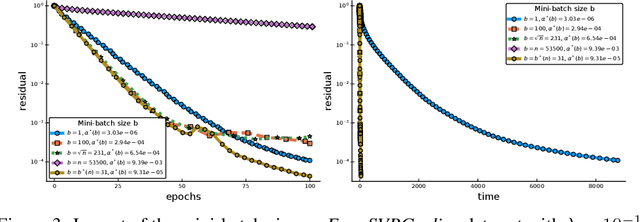
Abstract:Among the very first variance reduced stochastic methods for solving the empirical risk minimization problem was the SVRG method (Johnson & Zhang 2013). SVRG is an inner-outer loop based method, where in the outer loop a reference full gradient is evaluated, after which $m \in \mathbb{N}$ steps of an inner loop are executed where the reference gradient is used to build a variance reduced estimate of the current gradient. The simplicity of the SVRG method and its analysis has lead to multiple extensions and variants for even non-convex optimization. Yet there is a significant gap between the parameter settings that the analysis suggests and what is known to work well in practice. Our first contribution is that we take several steps towards closing this gap. In particular, the current analysis shows that $m$ should be of the order of the condition number so that the resulting method has a favorable complexity. Yet in practice $m =n$ works well irregardless of the condition number, where $n$ is the number of data points. Furthermore, the current analysis shows that the inner iterates have to be reset using averaging after every outer loop. Yet in practice SVRG works best when the inner iterates are updated continuously and not reset. We provide an analysis of these aforementioned practical settings and show that they achieve the same favorable complexity as the original analysis (with slightly better constants). Our second contribution is to provide a more general analysis than had been previously done by using arbitrary sampling, which allows us to analyse virtually all forms of mini-batching through a single theorem. Since our setup and analysis reflects what is done in practice, we are able to set the parameters such as the mini-batch size and step size using our theory in such a way that produces a more efficient algorithm in practice, as we show in extensive numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge