Reverse Markov Learning: Multi-Step Generative Models for Complex Distributions

Learning complex distributions is a fundamental challenge in contemporary applications. Generative models, such as diffusion models, have demonstrated remarkable success in overcoming many limitations of traditional statistical methods. Shen and Meinshausen (2024) introduced engression, a generative approach based on scoring rules that maps noise (and covariates, if available) directly to data. While effective, engression struggles with highly complex distributions, such as those encountered in image data. In this work, we extend engression to improve its capability in learning complex distributions. We propose a framework that defines a general forward process transitioning from the target distribution to a known distribution (e.g., Gaussian) and then learns a reverse Markov process using multiple engression models. This reverse process reconstructs the target distribution step by step. Our approach supports general forward processes, allows for dimension reduction, and naturally discretizes the generative process. As a special case, when using a diffusion-based forward process, our framework offers a method to discretize the training and inference of diffusion models efficiently. Empirical evaluations on simulated and climate data validate our theoretical insights, demonstrating the effectiveness of our approach in capturing complex distributions.

Distributional Instrumental Variable Method

The instrumental variable (IV) approach is commonly used to infer causal effects in the presence of unmeasured confounding. Conventional IV models commonly make the additive noise assumption, which is hard to ensure in practice, but also typically lack flexibility if the causal effects are complex. Further, the vast majority of the existing methods aims to estimate the mean causal effects only, a few other methods focus on the quantile effects. This work aims for estimation of the entire interventional distribution. We propose a novel method called distributional instrumental variables (DIV), which leverages generative modelling in a nonlinear instrumental variable setting. We establish identifiability of the interventional distribution under general assumptions and demonstrate an `under-identified' case where DIV can identify the causal effects while two-step least squares fails to. Our empirical results show that the DIV method performs well for a broad range of simulated data, exhibiting advantages over existing IV approaches in terms of the identifiability and estimation error of the mean or quantile treatment effects. Furthermore, we apply DIV to an economic data set to examine the causal relation between institutional quality and economic development and our results that closely align with the original study. We also apply DIV to a single-cell data set, where we study the generalizability and stability in predicting gene expression under unseen interventions. The software implementations of DIV are available in R and Python.

Distributional Principal Autoencoders

Dimension reduction techniques usually lose information in the sense that reconstructed data are not identical to the original data. However, we argue that it is possible to have reconstructed data identically distributed as the original data, irrespective of the retained dimension or the specific mapping. This can be achieved by learning a distributional model that matches the conditional distribution of data given its low-dimensional latent variables. Motivated by this, we propose Distributional Principal Autoencoder (DPA) that consists of an encoder that maps high-dimensional data to low-dimensional latent variables and a decoder that maps the latent variables back to the data space. For reducing the dimension, the DPA encoder aims to minimise the unexplained variability of the data with an adaptive choice of the latent dimension. For reconstructing data, the DPA decoder aims to match the conditional distribution of all data that are mapped to a certain latent value, thus ensuring that the reconstructed data retains the original data distribution. Our numerical results on climate data, single-cell data, and image benchmarks demonstrate the practical feasibility and success of the approach in reconstructing the original distribution of the data. DPA embeddings are shown to preserve meaningful structures of data such as the seasonal cycle for precipitations and cell types for gene expression.

Engression: Extrapolation for Nonlinear Regression?

Extrapolation is crucial in many statistical and machine learning applications, as it is common to encounter test data outside the training support. However, extrapolation is a considerable challenge for nonlinear models. Conventional models typically struggle in this regard: while tree ensembles provide a constant prediction beyond the support, neural network predictions tend to become uncontrollable. This work aims at providing a nonlinear regression methodology whose reliability does not break down immediately at the boundary of the training support. Our primary contribution is a new method called `engression' which, at its core, is a distributional regression technique for pre-additive noise models, where the noise is added to the covariates before applying a nonlinear transformation. Our experimental results indicate that this model is typically suitable for many real data sets. We show that engression can successfully perform extrapolation under some assumptions such as a strictly monotone function class, whereas traditional regression approaches such as least-squares regression and quantile regression fall short under the same assumptions. We establish the advantages of engression over existing approaches in terms of extrapolation, showing that engression consistently provides a meaningful improvement. Our empirical results, from both simulated and real data, validate these findings, highlighting the effectiveness of the engression method. The software implementations of engression are available in both R and Python.

Confidence and Uncertainty Assessment for Distributional Random Forests

The Distributional Random Forest (DRF) is a recently introduced Random Forest algorithm to estimate multivariate conditional distributions. Due to its general estimation procedure, it can be employed to estimate a wide range of targets such as conditional average treatment effects, conditional quantiles, and conditional correlations. However, only results about the consistency and convergence rate of the DRF prediction are available so far. We characterize the asymptotic distribution of DRF and develop a bootstrap approximation of it. This allows us to derive inferential tools for quantifying standard errors and the construction of confidence regions that have asymptotic coverage guarantees. In simulation studies, we empirically validate the developed theory for inference of low-dimensional targets and for testing distributional differences between two populations.

Robust detection and attribution of climate change under interventions

Fingerprints are key tools in climate change detection and attribution (D&A) that are used to determine whether changes in observations are different from internal climate variability (detection), and whether observed changes can be assigned to specific external drivers (attribution). We propose a direct D&A approach based on supervised learning to extract fingerprints that lead to robust predictions under relevant interventions on exogenous variables, i.e., climate drivers other than the target. We employ anchor regression, a distributionally-robust statistical learning method inspired by causal inference that extrapolates well to perturbed data under the interventions considered. The residuals from the prediction achieve either uncorrelatedness or mean independence with the exogenous variables, thus guaranteeing robustness. We define D&A as a unified hypothesis testing framework that relies on the same statistical model but uses different targets and test statistics. In the experiments, we first show that the CO2 forcing can be robustly predicted from temperature spatial patterns under strong interventions on the solar forcing. Second, we illustrate attribution to the greenhouse gases and aerosols while protecting against interventions on the aerosols and CO2 forcing, respectively. Our study shows that incorporating robustness constraints against relevant interventions may significantly benefit detection and attribution of climate change.

Scalable Sensitivity and Uncertainty Analysis for Causal-Effect Estimates of Continuous-Valued Interventions

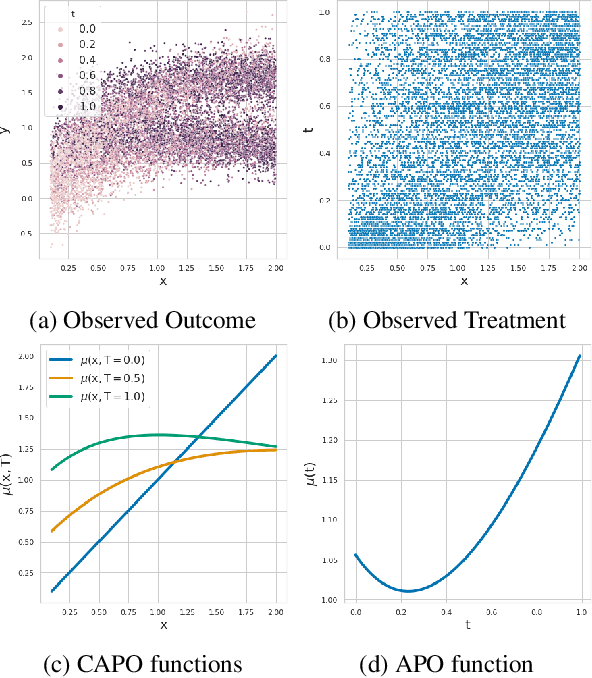
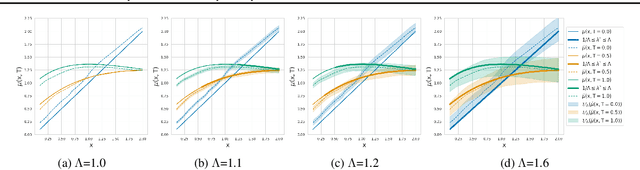
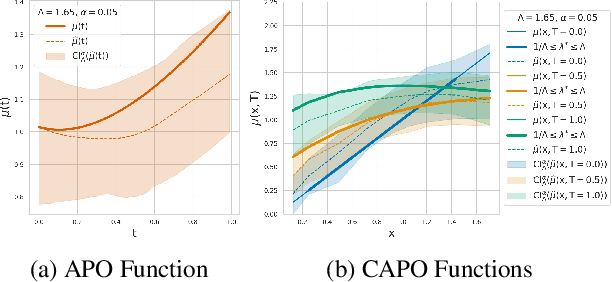
Estimating the effects of continuous-valued interventions from observational data is critically important in fields such as climate science, healthcare, and economics. Recent work focuses on designing neural-network architectures and regularization functions to allow for scalable estimation of average and individual-level dose response curves from high-dimensional, large-sample data. Such methodologies assume ignorability (all confounding variables are observed) and positivity (all levels of treatment can be observed for every unit described by a given covariate value), which are especially challenged in the continuous treatment regime. Developing scalable sensitivity and uncertainty analyses that allow us to understand the ignorance induced in our estimates when these assumptions are relaxed receives less attention. Here, we develop a continuous treatment-effect marginal sensitivity model (CMSM) and derive bounds that agree with both the observed data and a researcher-defined level of hidden confounding. We introduce a scalable algorithm to derive the bounds and uncertainty-aware deep models to efficiently estimate these bounds for high-dimensional, large-sample observational data. We validate our methods using both synthetic and real-world experiments. For the latter, we work in concert with climate scientists interested in evaluating the climatological impacts of human emissions on cloud properties using satellite observations from the past 15 years: a finite-data problem known to be complicated by the presence of a multitude of unobserved confounders.

fairadapt: Causal Reasoning for Fair Data Pre-processing

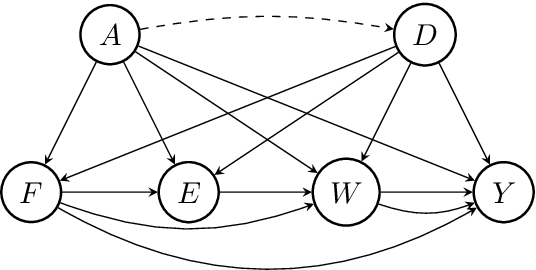
Machine learning algorithms are useful for various predictions tasks, but they can also learn how to discriminate, based on gender, race or other sensitive attributes. This realization gave rise to the field of fair machine learning, which aims to measure and mitigate such algorithmic bias. This manuscript describes the R-package fairadapt, which implements a causal inference pre-processing method. By making use of a causal graphical model and the observed data, the method can be used to address hypothetical questions of the form "What would my salary have been, had I been of a different gender/race?". Such individual level counterfactual reasoning can help eliminate discrimination and help justify fair decisions. We also discuss appropriate relaxations which assume certain causal pathways from the sensitive attribute to the outcome are not discriminatory.

Predicting sepsis in multi-site, multi-national intensive care cohorts using deep learning

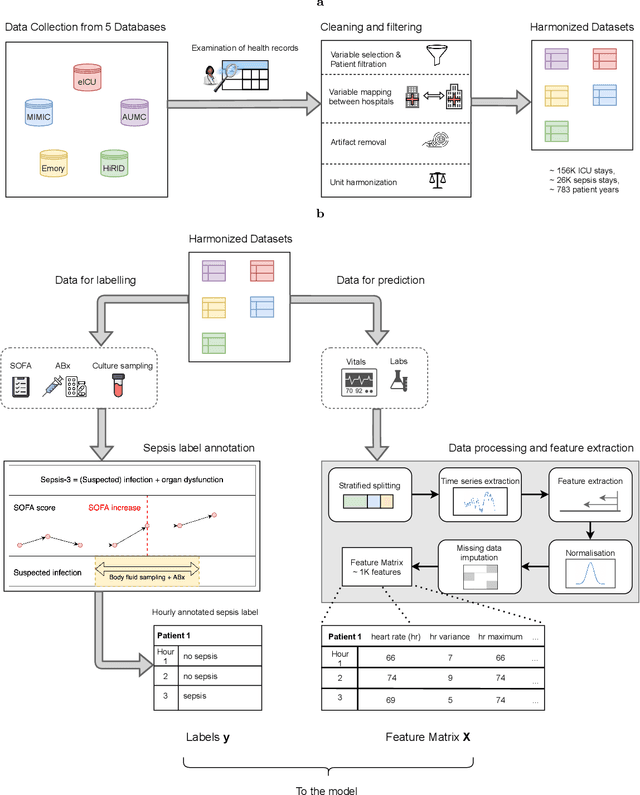
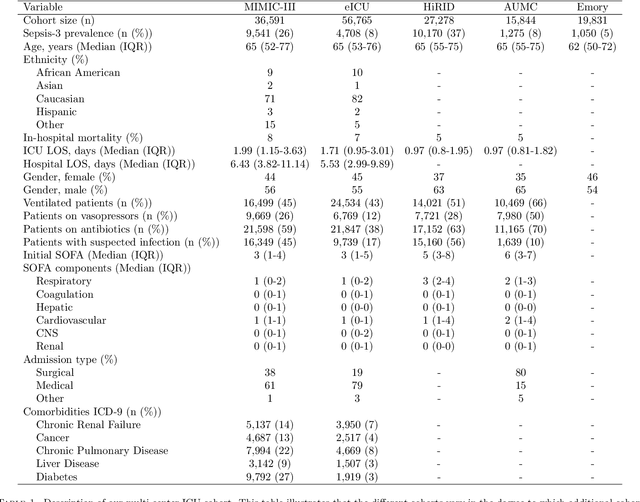
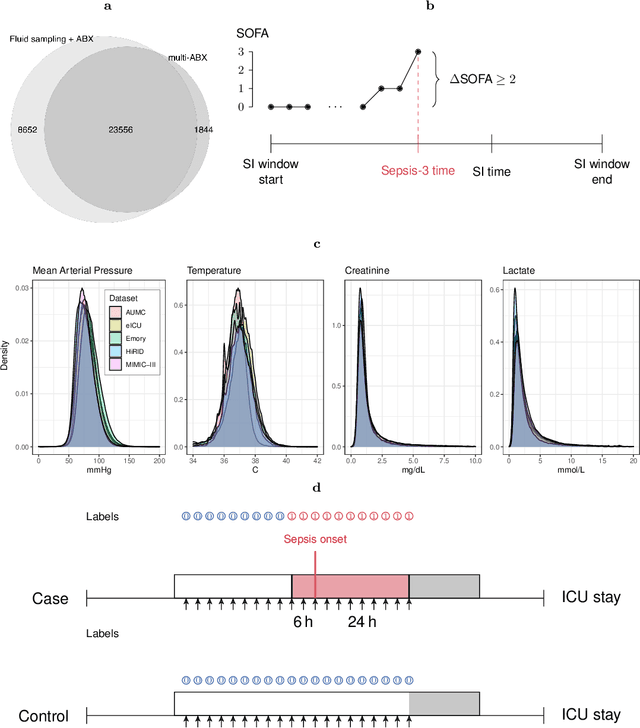
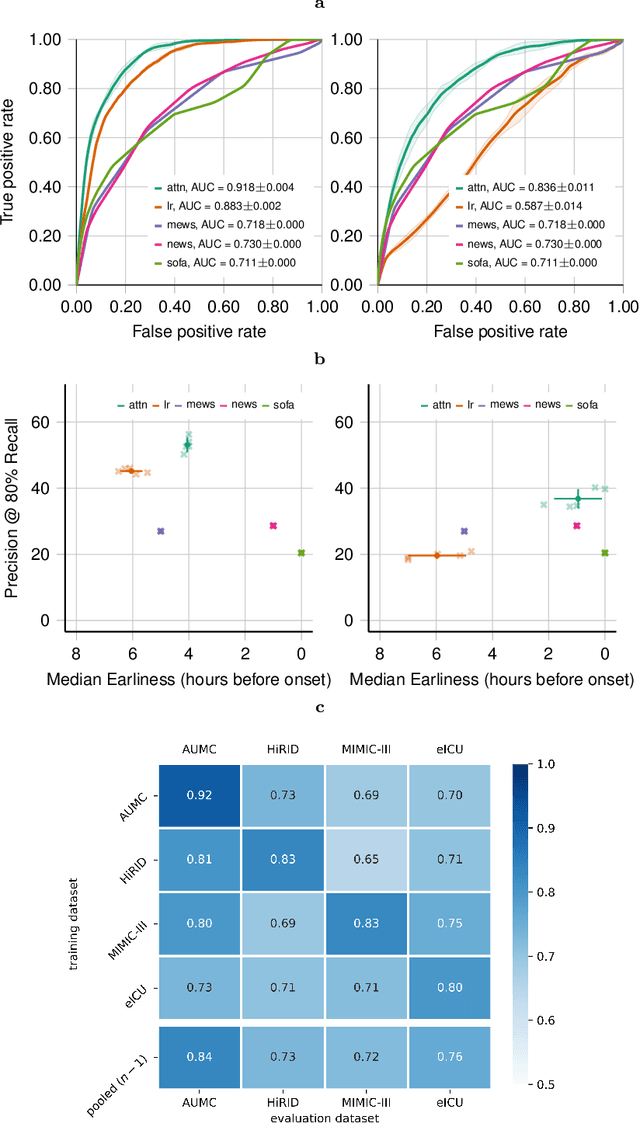
Despite decades of clinical research, sepsis remains a global public health crisis with high mortality, and morbidity. Currently, when sepsis is detected and the underlying pathogen is identified, organ damage may have already progressed to irreversible stages. Effective sepsis management is therefore highly time-sensitive. By systematically analysing trends in the plethora of clinical data available in the intensive care unit (ICU), an early prediction of sepsis could lead to earlier pathogen identification, resistance testing, and effective antibiotic and supportive treatment, and thereby become a life-saving measure. Here, we developed and validated a machine learning (ML) system for the prediction of sepsis in the ICU. Our analysis represents the largest multi-national, multi-centre in-ICU study for sepsis prediction using ML to date. Our dataset contains $156,309$ unique ICU admissions, which represent a refined and harmonised subset of five large ICU databases originating from three countries. Using the international consensus definition Sepsis-3, we derived hourly-resolved sepsis label annotations, amounting to $26,734$ ($17.1\%$) septic stays. We compared our approach, a deep self-attention model, to several clinical baselines as well as ML baselines and performed an extensive internal and external validation within and across databases. On average, our model was able to predict sepsis with an AUROC of $0.847 \pm 0.050$ (internal out-of sample validation) and $0.761 \pm 0.052$ (external validation). For a harmonised prevalence of $17\%$, at $80\%$ recall our model detects septic patients with $39\%$ precision 3.7 hours in advance.

Distributional Random Forests: Heterogeneity Adjustment and Multivariate Distributional Regression

We propose an adaptation of the Random Forest algorithm to estimate the conditional distribution of a possibly multivariate response. We suggest a new splitting criterion based on the MMD two-sample test, which is suitable for detecting heterogeneity in multivariate distributions. The weights provided by the forest can be conveniently used as an input to other methods in order to locally solve various learning problems. The code is available as \texttt{R}-package \texttt{drf}.