Robust detection and attribution of climate change under interventions

Fingerprints are key tools in climate change detection and attribution (D&A) that are used to determine whether changes in observations are different from internal climate variability (detection), and whether observed changes can be assigned to specific external drivers (attribution). We propose a direct D&A approach based on supervised learning to extract fingerprints that lead to robust predictions under relevant interventions on exogenous variables, i.e., climate drivers other than the target. We employ anchor regression, a distributionally-robust statistical learning method inspired by causal inference that extrapolates well to perturbed data under the interventions considered. The residuals from the prediction achieve either uncorrelatedness or mean independence with the exogenous variables, thus guaranteeing robustness. We define D&A as a unified hypothesis testing framework that relies on the same statistical model but uses different targets and test statistics. In the experiments, we first show that the CO2 forcing can be robustly predicted from temperature spatial patterns under strong interventions on the solar forcing. Second, we illustrate attribution to the greenhouse gases and aerosols while protecting against interventions on the aerosols and CO2 forcing, respectively. Our study shows that incorporating robustness constraints against relevant interventions may significantly benefit detection and attribution of climate change.

An information-geometric approach to feature extraction and moment reconstruction in dynamical systems

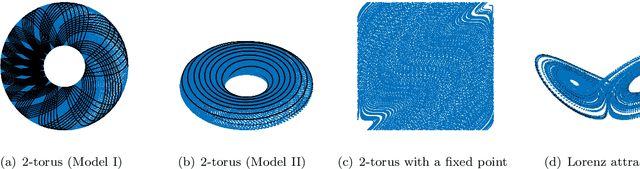
We propose a dimension reduction framework for feature extraction and moment reconstruction in dynamical systems that operates on spaces of probability measures induced by observables of the system rather than directly in the original data space of the observables themselves as in more conventional methods. Our approach is based on the fact that orbits of a dynamical system induce probability measures over the measurable space defined by (partial) observations of the system. We equip the space of these probability measures with a divergence, i.e., a distance between probability distributions, and use this divergence to define a kernel integral operator. The eigenfunctions of this operator create an orthonormal basis of functions that capture different timescales of the dynamical system. One of our main results shows that the evolution of the moments of the dynamics-dependent probability measures can be related to a time-averaging operator on the original dynamical system. Using this result, we show that the moments can be expanded in the eigenfunction basis, thus opening up the avenue for nonparametric forecasting of the moments. If the collection of probability measures is itself a manifold, we can in addition equip the statistical manifold with the Riemannian metric and use techniques from information geometry. We present applications to ergodic dynamical systems on the 2-torus and the Lorenz 63 system, and show on a real-world example that a small number of eigenvectors is sufficient to reconstruct the moments (here the first four moments) of an atmospheric time series, i.e., the realtime multivariate Madden-Julian oscillation index.