Efficient algorithms for regularized Poisson Non-negative Matrix Factorization

We consider the problem of regularized Poisson Non-negative Matrix Factorization (NMF) problem, encompassing various regularization terms such as Lipschitz and relatively smooth functions, alongside linear constraints. This problem holds significant relevance in numerous Machine Learning applications, particularly within the domain of physical linear unmixing problems. A notable challenge arises from the main loss term in the Poisson NMF problem being a KL divergence, which is non-Lipschitz, rendering traditional gradient descent-based approaches inefficient. In this contribution, we explore the utilization of Block Successive Upper Minimization (BSUM) to overcome this challenge. We build approriate majorizing function for Lipschitz and relatively smooth functions, and show how to introduce linear constraints into the problem. This results in the development of two novel algorithms for regularized Poisson NMF. We conduct numerical simulations to showcase the effectiveness of our approach.

Laue Indexing with Optimal Transport

Laue tomography experiments retrieve the positions and orientations of crystal grains in a polycrystalline samples from diffraction patterns recorded at multiple viewing angles. The use of a broad wavelength spectrum beam can greatly reduce the experimental time, but poses a difficult challenge for the indexing of diffraction peaks in polycrystalline samples; the information about the wavelength of these Bragg peaks is absent and the diffraction patterns from multiple grains are superimposed. To date, no algorithms exist capable of indexing samples with more than about 500 grains efficiently. To address this need we present a novel method: Laue indexing with Optimal Transport (LaueOT). We create a probabilistic description of the multi-grain indexing problem and propose a solution based on Sinkhorn Expectation-Maximization method, which allows to efficiently find the maximum of the likelihood thanks to the assignments being calculated using Optimal Transport. This is a non-convex optimization problem, where the orientations and positions of grains are optimized simultaneously with grain-to-spot assignments, while robustly handling the outliers. The selection of initial prototype grains to consider in the optimization problem are also calculated within the Optimal Transport framework. LaueOT can rapidly and effectively index up to 1000 grains on a single large memory GPU within less than 30 minutes. We demonstrate the performance of LaueOT on simulations with variable numbers of grains, spot position measurement noise levels, and outlier fractions. The algorithm recovers the correct number of grains even for high noise levels and up to 70% outliers in our experiments. We compare the results of indexing with LaueOT to existing algorithms both on synthetic and real neutron diffraction data from well-characterized samples.

An evaluation of deep learning models for predicting water depth evolution in urban floods

In this technical report we compare different deep learning models for prediction of water depth rasters at high spatial resolution. Efficient, accurate, and fast methods for water depth prediction are nowadays important as urban floods are increasing due to higher rainfall intensity caused by climate change, expansion of cities and changes in land use. While hydrodynamic models models can provide reliable forecasts by simulating water depth at every location of a catchment, they also have a high computational burden which jeopardizes their application to real-time prediction in large urban areas at high spatial resolution. Here, we propose to address this issue by using data-driven techniques. Specifically, we evaluate deep learning models which are trained to reproduce the data simulated by the CADDIES cellular-automata flood model, providing flood forecasts that can occur at different future time horizons. The advantage of using such models is that they can learn the underlying physical phenomena a priori, preventing manual parameter setting and computational burden. We perform experiments on a dataset consisting of two catchments areas within Switzerland with 18 simpler, short rainfall patterns and 4 long, more complex ones. Our results show that the deep learning models present in general lower errors compared to the other methods, especially for water depths $>0.5m$. However, when testing on more complex rainfall events or unseen catchment areas, the deep models do not show benefits over the simpler ones.

Optirank: classification for RNA-Seq data with optimal ranking reference genes

Classification algorithms using RNA-Sequencing (RNA-Seq) data as input are used in a variety of biological applications. By nature, RNA-Seq data is subject to uncontrolled fluctuations both within and especially across datasets, which presents a major difficulty for a trained classifier to generalize to an external dataset. Replacing raw gene counts with the rank of gene counts inside an observation has proven effective to mitigate this problem. However, the rank of a feature is by definition relative to all other features, including highly variable features that introduce noise in the ranking. To address this problem and obtain more robust ranks, we propose a logistic regression model, optirank, which learns simultaneously the parameters of the model and the genes to use as a reference set in the ranking. We show the effectiveness of this method on simulated data. We also consider real classification tasks, which present different kinds of distribution shifts between train and test data. Those tasks concern a variety of applications, such as cancer of unknown primary classification, identification of specific gene signatures, and determination of cell type in single-cell RNA-Seq datasets. On those real tasks, optirank performs at least as well as the vanilla logistic regression on classical ranks, while producing sparser solutions. In addition, to increase the robustness against dataset shifts, we propose a multi-source learning scheme and demonstrate its effectiveness when used in combination with rank-based classifiers.

Robust detection and attribution of climate change under interventions

Fingerprints are key tools in climate change detection and attribution (D&A) that are used to determine whether changes in observations are different from internal climate variability (detection), and whether observed changes can be assigned to specific external drivers (attribution). We propose a direct D&A approach based on supervised learning to extract fingerprints that lead to robust predictions under relevant interventions on exogenous variables, i.e., climate drivers other than the target. We employ anchor regression, a distributionally-robust statistical learning method inspired by causal inference that extrapolates well to perturbed data under the interventions considered. The residuals from the prediction achieve either uncorrelatedness or mean independence with the exogenous variables, thus guaranteeing robustness. We define D&A as a unified hypothesis testing framework that relies on the same statistical model but uses different targets and test statistics. In the experiments, we first show that the CO2 forcing can be robustly predicted from temperature spatial patterns under strong interventions on the solar forcing. Second, we illustrate attribution to the greenhouse gases and aerosols while protecting against interventions on the aerosols and CO2 forcing, respectively. Our study shows that incorporating robustness constraints against relevant interventions may significantly benefit detection and attribution of climate change.

Empirical Bayes Transductive Meta-Learning with Synthetic Gradients

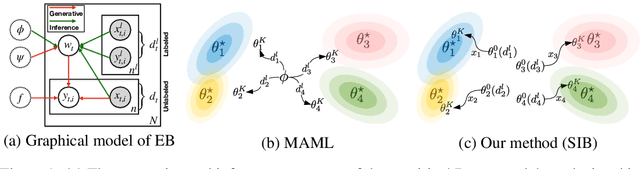
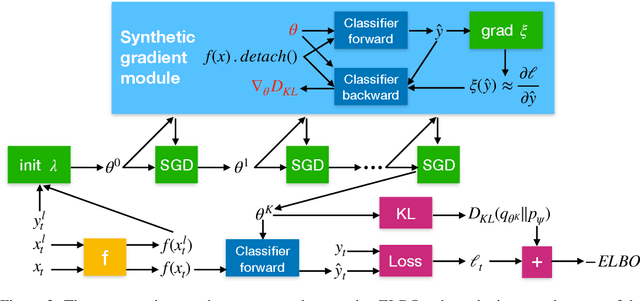
We propose a meta-learning approach that learns from multiple tasks in a transductive setting, by leveraging the unlabeled query set in addition to the support set to generate a more powerful model for each task. To develop our framework, we revisit the empirical Bayes formulation for multi-task learning. The evidence lower bound of the marginal log-likelihood of empirical Bayes decomposes as a sum of local KL divergences between the variational posterior and the true posterior on the query set of each task. We derive a novel amortized variational inference that couples all the variational posteriors via a meta-model, which consists of a synthetic gradient network and an initialization network. Each variational posterior is derived from synthetic gradient descent to approximate the true posterior on the query set, although where we do not have access to the true gradient. Our results on the Mini-ImageNet and CIFAR-FS benchmarks for episodic few-shot classification outperform previous state-of-the-art methods. Besides, we conduct two zero-shot learning experiments to further explore the potential of the synthetic gradient.

Tensor Decompositions for temporal knowledge base completion

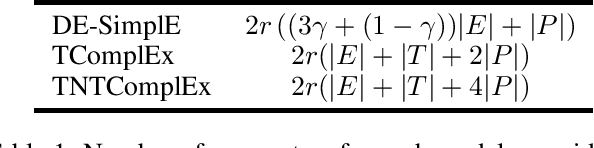
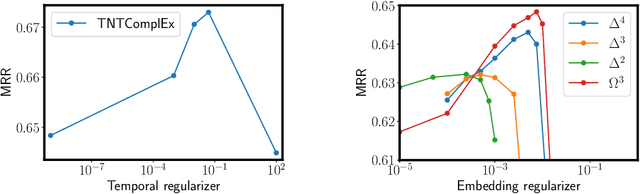
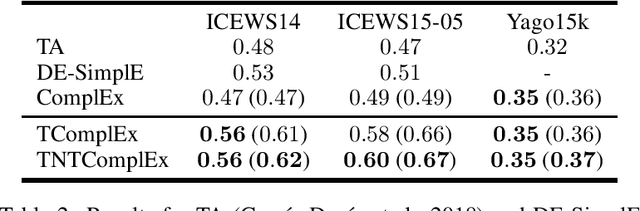
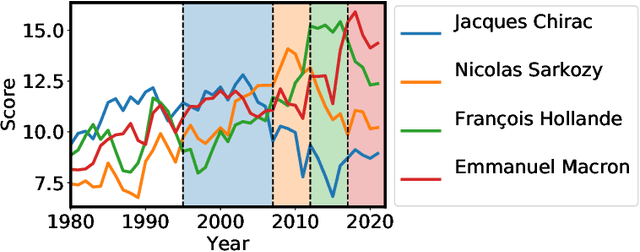
Most algorithms for representation learning and link prediction in relational data have been designed for static data. However, the data they are applied to usually evolves with time, such as friend graphs in social networks or user interactions with items in recommender systems. This is also the case for knowledge bases, which contain facts such as (US, has president, B. Obama, [2009-2017]) that are valid only at certain points in time. For the problem of link prediction under temporal constraints, i.e., answering queries such as (US, has president, ?, 2012), we propose a solution inspired by the canonical decomposition of tensors of order 4. We introduce new regularization schemes and present an extension of ComplEx (Trouillon et al., 2016) that achieves state-of-the-art performance. Additionally, we propose a new dataset for knowledge base completion constructed from Wikidata, larger than previous benchmarks by an order of magnitude, as a new reference for evaluating temporal and non-temporal link prediction methods.

Learning the effect of latent variables in Gaussian Graphical models with unobserved variables

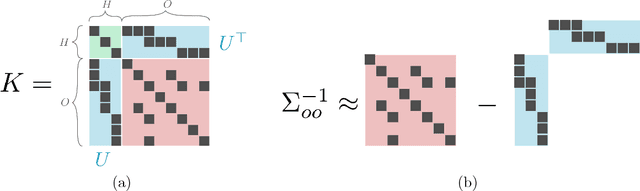
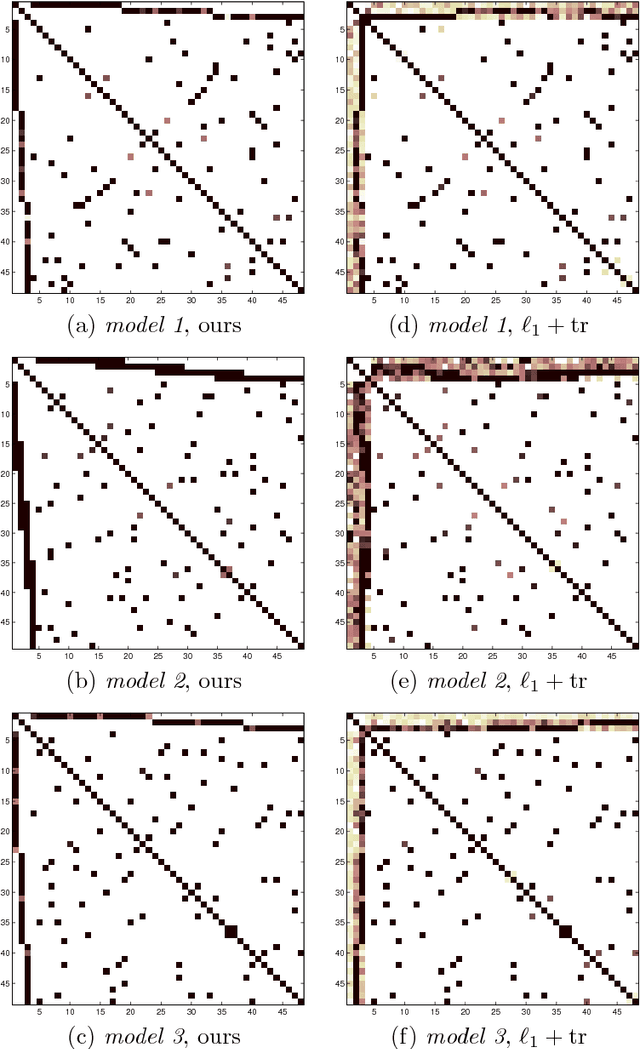
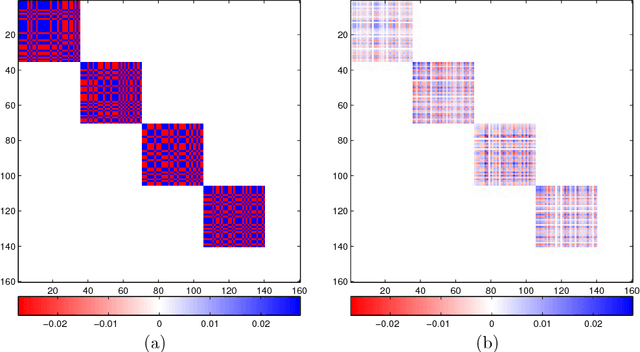
The edge structure of the graph defining an undirected graphical model describes precisely the structure of dependence between the variables in the graph. In many applications, the dependence structure is unknown and it is desirable to learn it from data, often because it is a preliminary step to be able to ascertain causal effects. This problem, known as structure learning, is hard in general, but for Gaussian graphical models it is slightly easier because the structure of the graph is given by the sparsity pattern of the precision matrix of the joint distribution, and because independence coincides with decorrelation. A major difficulty too often ignored in structure learning is the fact that if some variables are not observed, the marginal dependence graph over the observed variables will possibly be significantly more complex and no longer reflect the direct dependencies that are potentially associated with causal effects. In this work, we consider a family of latent variable Gaussian graphical models in which the graph of the joint distribution between observed and unobserved variables is sparse, and the unobserved variables are conditionally independent given the others. Prior work was able to recover the connectivity between observed variables, but could only identify the subspace spanned by unobserved variables, whereas we propose a convex optimization formulation based on structured matrix sparsity to estimate the complete connectivity of the complete graph including unobserved variables, given the knowledge of the number of missing variables, and a priori knowledge of their level of connectivity. Our formulation is supported by a theoretical result of identifiability of the latent dependence structure for sparse graphs in the infinite data limit. We propose an algorithm leveraging recent active set methods, which performs well in the experiments on synthetic data.

Canonical Tensor Decomposition for Knowledge Base Completion

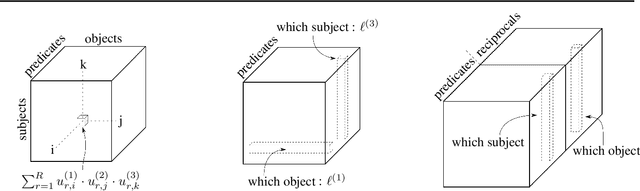
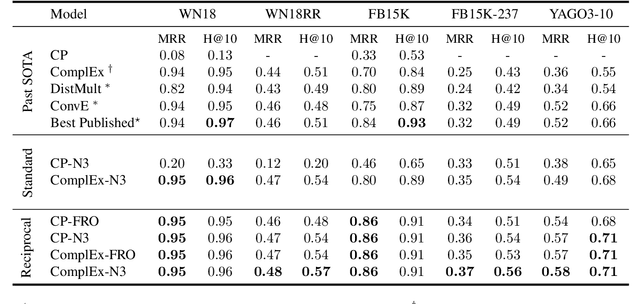
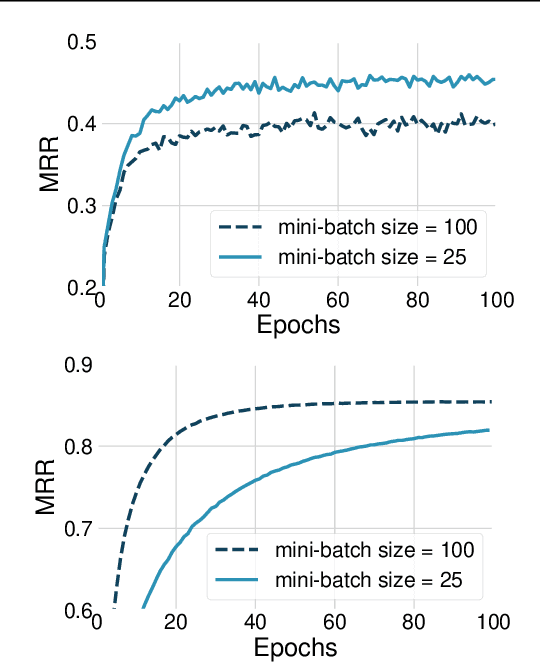
The problem of Knowledge Base Completion can be framed as a 3rd-order binary tensor completion problem. In this light, the Canonical Tensor Decomposition (CP) (Hitchcock, 1927) seems like a natural solution; however, current implementations of CP on standard Knowledge Base Completion benchmarks are lagging behind their competitors. In this work, we attempt to understand the limits of CP for knowledge base completion. First, we motivate and test a novel regularizer, based on tensor nuclear $p$-norms. Then, we present a reformulation of the problem that makes it invariant to arbitrary choices in the inclusion of predicates or their reciprocals in the dataset. These two methods combined allow us to beat the current state of the art on several datasets with a CP decomposition, and obtain even better results using the more advanced ComplEx model.

Tight convex relaxations for sparse matrix factorization

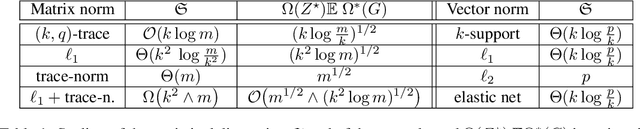
Based on a new atomic norm, we propose a new convex formulation for sparse matrix factorization problems in which the number of nonzero elements of the factors is assumed fixed and known. The formulation counts sparse PCA with multiple factors, subspace clustering and low-rank sparse bilinear regression as potential applications. We compute slow rates and an upper bound on the statistical dimension of the suggested norm for rank 1 matrices, showing that its statistical dimension is an order of magnitude smaller than the usual $\ell\_1$-norm, trace norm and their combinations. Even though our convex formulation is in theory hard and does not lead to provably polynomial time algorithmic schemes, we propose an active set algorithm leveraging the structure of the convex problem to solve it and show promising numerical results.