A Regret Minimization Approach to Iterative Learning Control

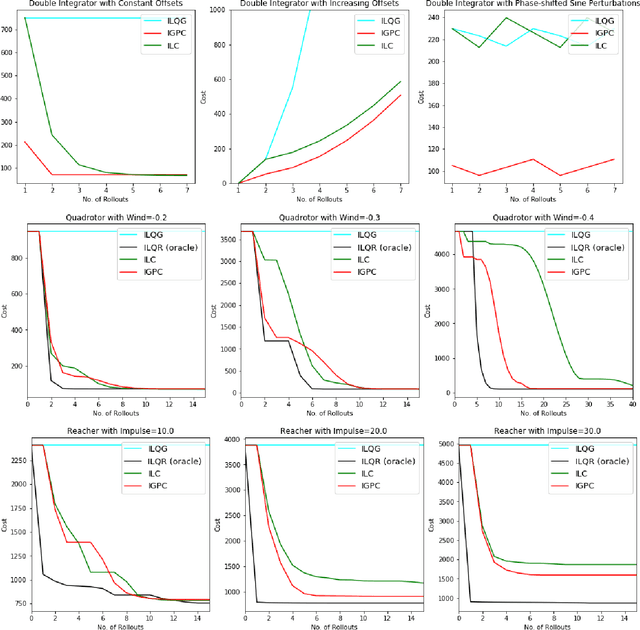
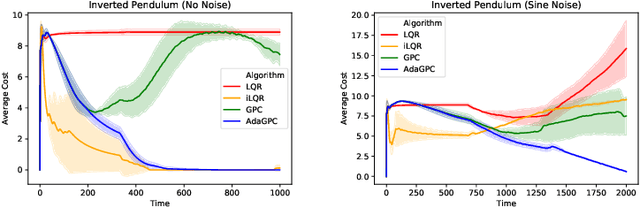
We consider the setting of iterative learning control, or model-based policy learning in the presence of uncertain, time-varying dynamics. In this setting, we propose a new performance metric, planning regret, which replaces the standard stochastic uncertainty assumptions with worst case regret. Based on recent advances in non-stochastic control, we design a new iterative algorithm for minimizing planning regret that is more robust to model mismatch and uncertainty. We provide theoretical and empirical evidence that the proposed algorithm outperforms existing methods on several benchmarks.

Deluca -- A Differentiable Control Library: Environments, Methods, and Benchmarking

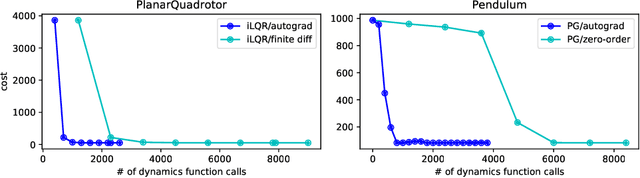
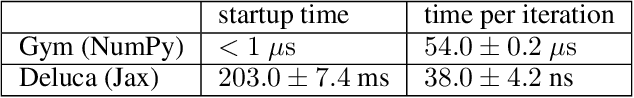
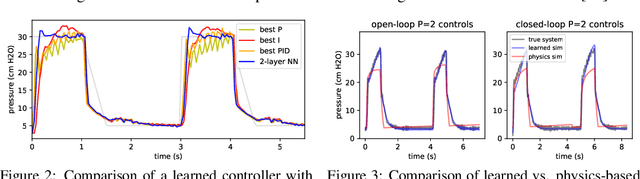
We present an open-source library of natively differentiable physics and robotics environments, accompanied by gradient-based control methods and a benchmark-ing suite. The introduced environments allow auto-differentiation through the simulation dynamics, and thereby permit fast training of controllers. The library features several popular environments, including classical control settings from OpenAI Gym. We also provide a novel differentiable environment, based on deep neural networks, that simulates medical ventilation. We give several use-cases of new scientific results obtained using the library. This includes a medical ventilator simulator and controller, an adaptive control method for time-varying linear dynamical systems, and new gradient-based methods for control of linear dynamical systems with adversarial perturbations.

Stochastic Optimization with Laggard Data Pipelines

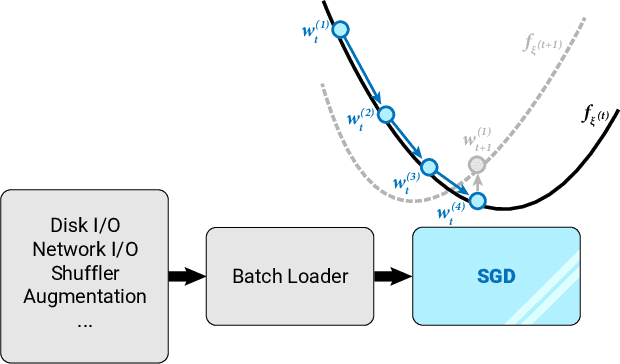
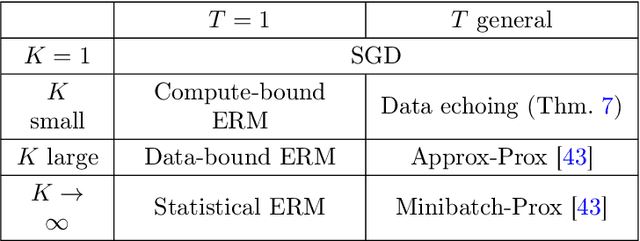
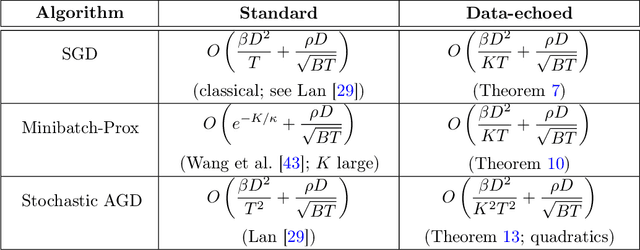
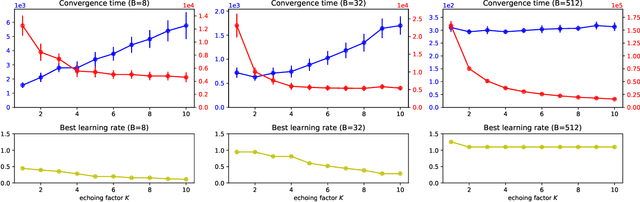
State-of-the-art optimization is steadily shifting towards massively parallel pipelines with extremely large batch sizes. As a consequence, CPU-bound preprocessing and disk/memory/network operations have emerged as new performance bottlenecks, as opposed to hardware-accelerated gradient computations. In this regime, a recently proposed approach is data echoing (Choi et al., 2019), which takes repeated gradient steps on the same batch while waiting for fresh data to arrive from upstream. We provide the first convergence analyses of "data-echoed" extensions of common optimization methods, showing that they exhibit provable improvements over their synchronous counterparts. Specifically, we show that in convex optimization with stochastic minibatches, data echoing affords speedups on the curvature-dominated part of the convergence rate, while maintaining the optimal statistical rate.

Disentangling Adaptive Gradient Methods from Learning Rates

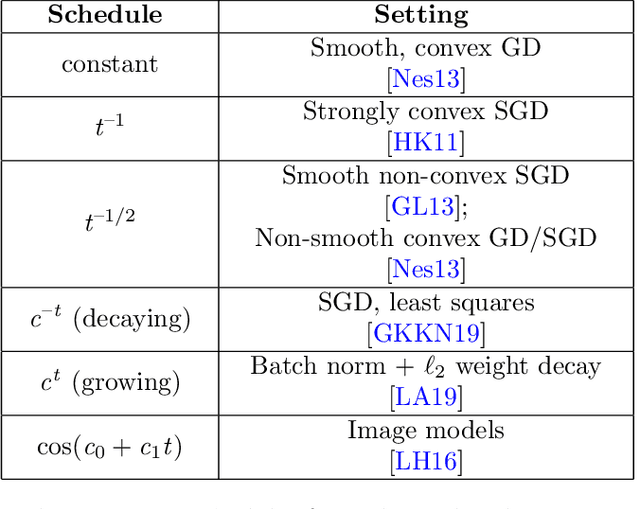
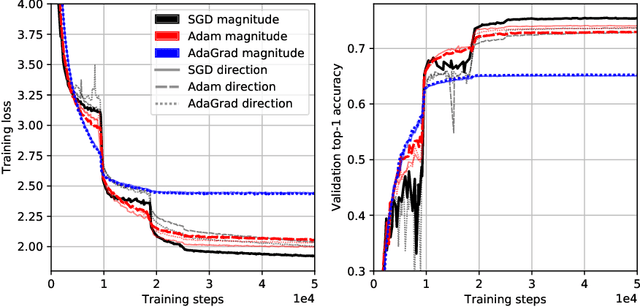
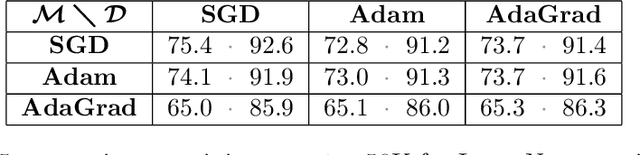
We investigate several confounding factors in the evaluation of optimization algorithms for deep learning. Primarily, we take a deeper look at how adaptive gradient methods interact with the learning rate schedule, a notoriously difficult-to-tune hyperparameter which has dramatic effects on the convergence and generalization of neural network training. We introduce a "grafting" experiment which decouples an update's magnitude from its direction, finding that many existing beliefs in the literature may have arisen from insufficient isolation of the implicit schedule of step sizes. Alongside this contribution, we present some empirical and theoretical retrospectives on the generalization of adaptive gradient methods, aimed at bringing more clarity to this space.

A Deep Conditioning Treatment of Neural Networks

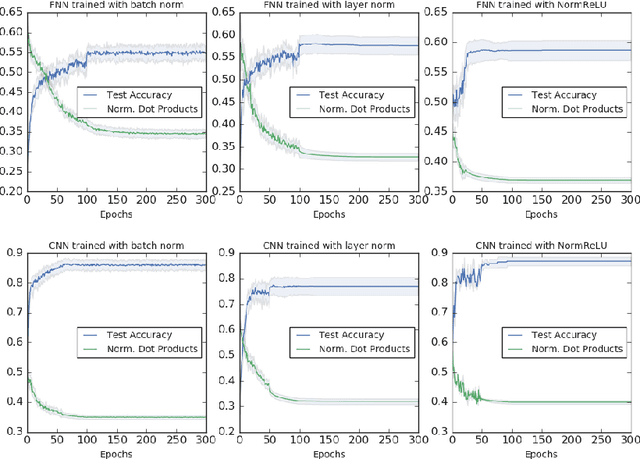
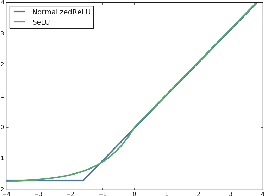
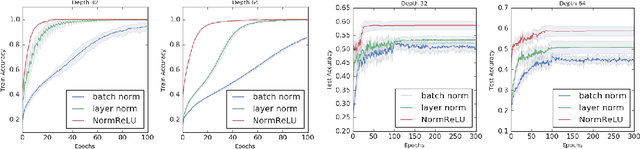
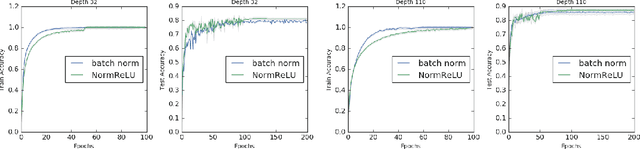
We study the role of depth in training randomly initialized overparameterized neural networks. We give the first general result showing that depth improves trainability of neural networks by improving the {\em conditioning} of certain kernel matrices of the input data. This result holds for arbitrary non-linear activation functions, and we provide a characterization of the improvement in conditioning as a function of the degree of non-linearity and the depth of the network. We provide versions of the result that hold for training just the top layer of the neural network, as well as for training all layers, via the neural tangent kernel. As applications of these general results, we provide a generalization of the results of Das et al. (2019) showing that learnability of deep random neural networks with arbitrary non-linear activations (under mild assumptions) degrades exponentially with depth. Additionally, we show how benign overfitting can occur in deep neural networks via the results of Bartlett et al. (2019b).

Logarithmic Regret for Online Control

We study optimal regret bounds for control in linear dynamical systems under adversarially changing strongly convex cost functions, given the knowledge of transition dynamics. This includes several well studied and fundamental frameworks such as the Kalman filter and the linear quadratic regulator. State of the art methods achieve regret which scales as $O(\sqrt{T})$, where $T$ is the time horizon. We show that the optimal regret in this setting can be significantly smaller, scaling as $O(\text{poly}(\log T))$. This regret bound is achieved by two different efficient iterative methods, online gradient descent and online natural gradient.

Boosting for Dynamical Systems

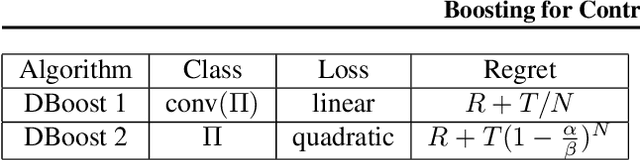
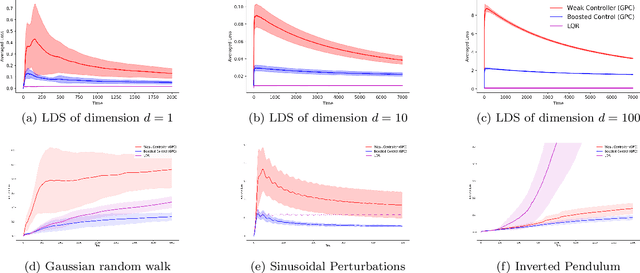
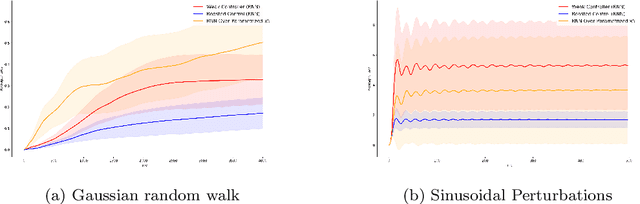
We propose a framework of boosting for learning and control in environments that maintain a state. Leveraging methods for online learning with memory and for online boosting, we design an efficient online algorithm that can provably improve the accuracy of weak-learners in stateful environments. As a consequence, we give efficient boosting algorithms for both prediction and the control of dynamical systems. Empirical evaluation on simulated and real data for both control and prediction supports our theoretical findings.

Design and Development of Underwater Vehicle: ANAHITA

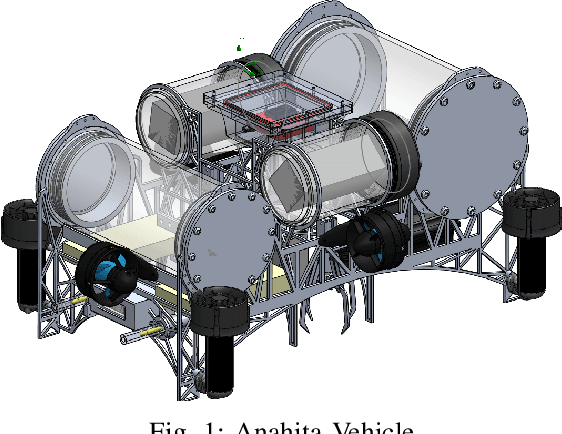
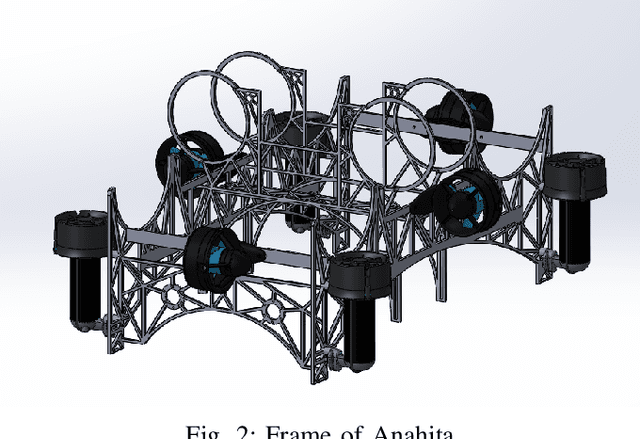
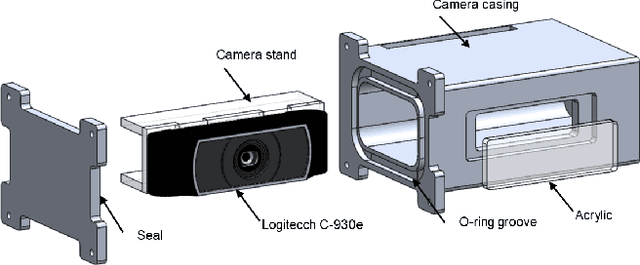
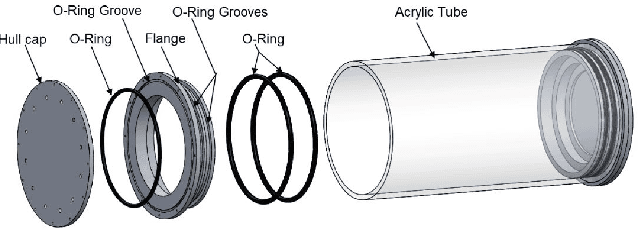
Anahita is an autonomous underwater vehicle which is currently being developed by interdisciplinary team of students at Indian Institute of Technology(IIT) Kanpur with aim to provide a platform for research in AUV to undergraduate students. This is the second vehicle which is being designed by AUV-IITK team to participate in 6th NIOT-SAVe competition organized by the National Institute of Ocean Technology, Chennai. The Vehicle has been completely redesigned with the major improvements in modularity and ease of access of all the components, keeping the design very compact and efficient. New advancements in the vehicle include, power distribution system and monitoring system. The sensors include the inertial measurement units (IMU), hydrophone array, a depth sensor, and two RGB cameras. The current vehicle features hot swappable battery pods giving a huge advantage over the previous vehicle, for longer runtime.

Online Control with Adversarial Disturbances

We study the control of a linear dynamical system with adversarial disturbances (as opposed to statistical noise). The objective we consider is one of regret: we desire an online control procedure that can do nearly as well as that of a procedure that has full knowledge of the disturbances in hindsight. Our main result is an efficient algorithm that provides nearly tight regret bounds for this problem. From a technical standpoint, this work generalizes upon previous work in two main aspects: our model allows for adversarial noise in the dynamics, and allows for general convex costs.

Extreme Tensoring for Low-Memory Preconditioning

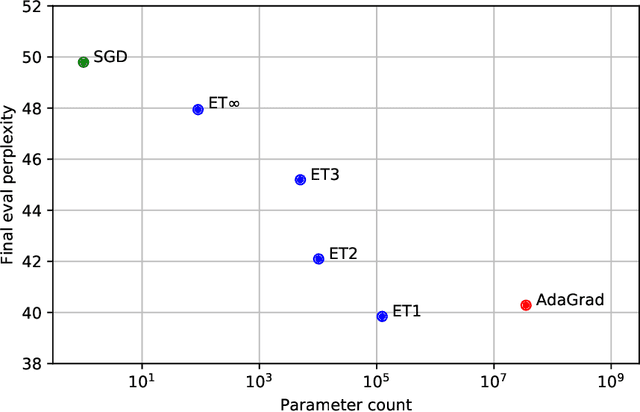
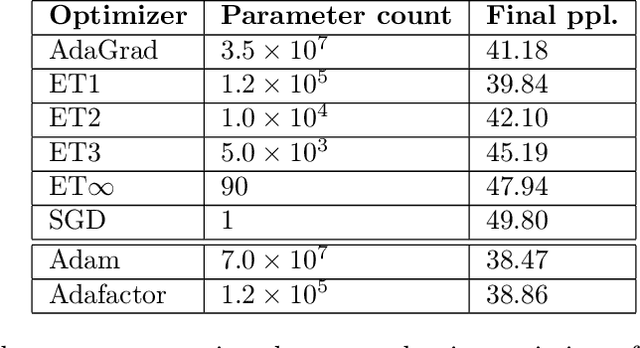
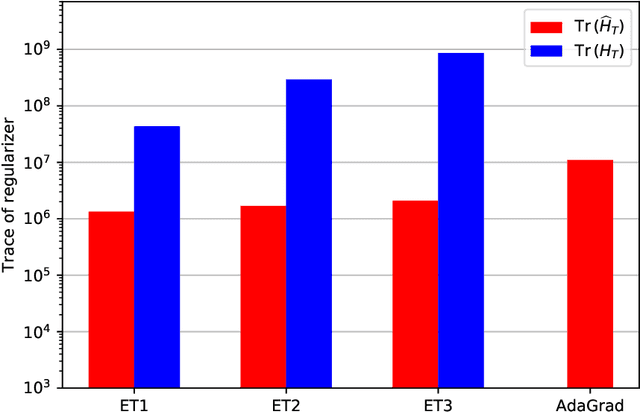
State-of-the-art models are now trained with billions of parameters, reaching hardware limits in terms of memory consumption. This has created a recent demand for memory-efficient optimizers. To this end, we investigate the limits and performance tradeoffs of memory-efficient adaptively preconditioned gradient methods. We propose extreme tensoring for high-dimensional stochastic optimization, showing that an optimizer needs very little memory to benefit from adaptive preconditioning. Our technique applies to arbitrary models (not necessarily with tensor-shaped parameters), and is accompanied by regret and convergence guarantees, which shed light on the tradeoffs between preconditioner quality and expressivity. On a large-scale NLP model, we reduce the optimizer memory overhead by three orders of magnitude, without degrading performance.