Training-Free Self-Correction for Multimodal Masked Diffusion Models

Masked diffusion models have emerged as a powerful framework for text and multimodal generation. However, their sampling procedure updates multiple tokens simultaneously and treats generated tokens as immutable, which may lead to error accumulation when early mistakes cannot be revised. In this work, we revisit existing self-correction methods and identify limitations stemming from additional training requirements or reliance on misaligned likelihood estimates. We propose a training-free self-correction framework that exploits the inductive biases of pre-trained masked diffusion models. Without modifying model parameters or introducing auxiliary evaluators, our method significantly improves generation quality on text-to-image generation and multimodal understanding tasks with reduced sampling steps. Moreover, the proposed framework generalizes across different masked diffusion architectures, highlighting its robustness and practical applicability. Code can be found in https://github.com/huge123/FreeCorrection.

Corrected Samplers for Discrete Flow Models

Discrete flow models (DFMs) have been proposed to learn the data distribution on a finite state space, offering a flexible framework as an alternative to discrete diffusion models. A line of recent work has studied samplers for discrete diffusion models, such as tau-leaping and Euler solver. However, these samplers require a large number of iterations to control discretization error, since the transition rates are frozen in time and evaluated at the initial state within each time interval. Moreover, theoretical results for these samplers often require boundedness conditions of the transition rate or they focus on a specific type of source distributions. To address those limitations, we establish non-asymptotic discretization error bounds for those samplers without any restriction on transition rates and source distributions, under the framework of discrete flow models. Furthermore, by analyzing a one-step lower bound of the Euler sampler, we propose two corrected samplers: \textit{time-corrected sampler} and \textit{location-corrected sampler}, which can reduce the discretization error of tau-leaping and Euler solver with almost no additional computational cost. We rigorously show that the location-corrected sampler has a lower iteration complexity than existing parallel samplers. We validate the effectiveness of the proposed method by demonstrating improved generation quality and reduced inference time on both simulation and text-to-image generation tasks. Code can be found in https://github.com/WanZhengyan/Corrected-Samplers-for-Discrete-Flow-Models.

Error Analysis of Discrete Flow with Generator Matching

Discrete flow models offer a powerful framework for learning distributions over discrete state spaces and have demonstrated superior performance compared to the discrete diffusion model. However, their convergence properties and error analysis remain largely unexplored. In this work, we develop a unified framework grounded in stochastic calculus theory to systematically investigate the theoretical properties of discrete flow. Specifically, we derive the KL divergence of two path measures regarding two continuous-time Markov chains (CTMCs) with different transition rates by developing a novel Girsanov-type theorem, and provide a comprehensive analysis that encompasses the error arising from transition rate estimation and early stopping, where the first type of error has rarely been analyzed by existing works. Unlike discrete diffusion models, discrete flow incurs no truncation error caused by truncating the time horizon in the noising process. Building on generator matching and uniformization, we establish non-asymptotic error bounds for distribution estimation. Our results provide the first error analysis for discrete flow models.

Discrete Guidance Matching: Exact Guidance for Discrete Flow Matching

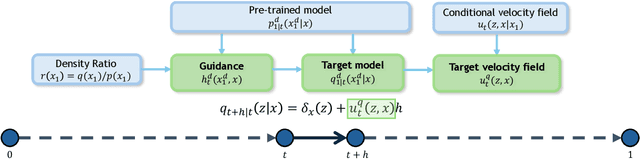
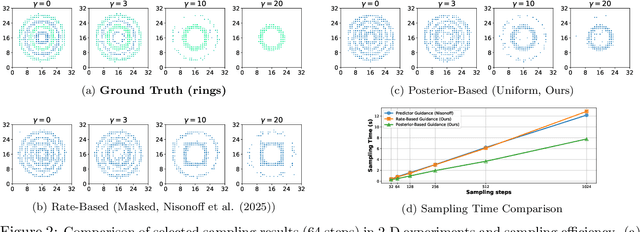
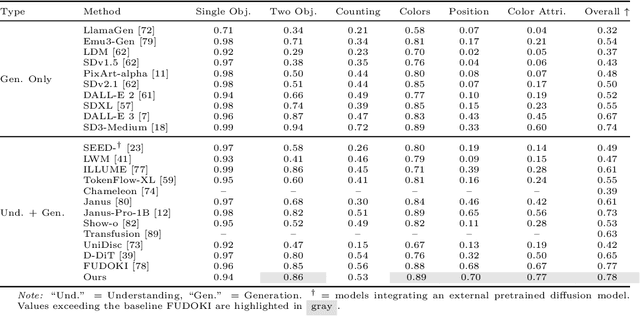
Guidance provides a simple and effective framework for posterior sampling by steering the generation process towards the desired distribution. When modeling discrete data, existing approaches mostly focus on guidance with the first-order Taylor approximation to improve the sampling efficiency. However, such an approximation is inappropriate in discrete state spaces since the approximation error could be large. A novel guidance framework for discrete data is proposed to address this problem: We derive the exact transition rate for the desired distribution given a learned discrete flow matching model, leading to guidance that only requires a single forward pass in each sampling step, significantly improving efficiency. This unified novel framework is general enough, encompassing existing guidance methods as special cases, and it can also be seamlessly applied to the masked diffusion model. We demonstrate the effectiveness of our proposed guidance on energy-guided simulations and preference alignment on text-to-image generation and multimodal understanding tasks. The code is available through https://github.com/WanZhengyan/Discrete-Guidance-Matching/tree/main.