Results of the Big ANN: NeurIPS'23 competition

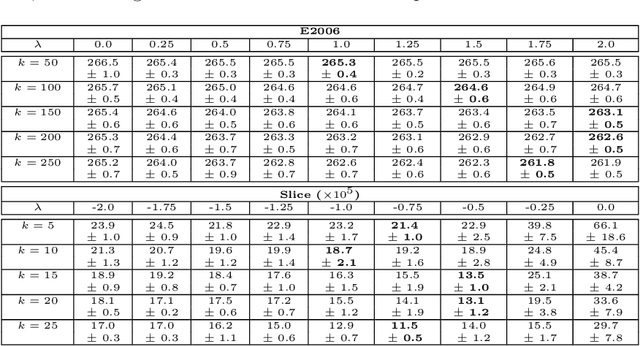
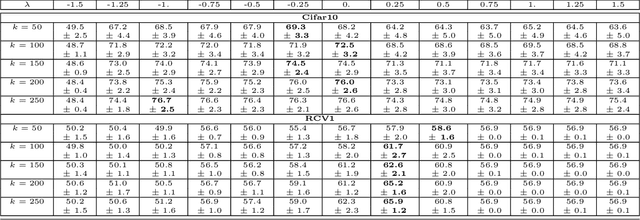
The 2023 Big ANN Challenge, held at NeurIPS 2023, focused on advancing the state-of-the-art in indexing data structures and search algorithms for practical variants of Approximate Nearest Neighbor (ANN) search that reflect the growing complexity and diversity of workloads. Unlike prior challenges that emphasized scaling up classical ANN search ~\cite{DBLP:conf/nips/SimhadriWADBBCH21}, this competition addressed filtered search, out-of-distribution data, sparse and streaming variants of ANNS. Participants developed and submitted innovative solutions that were evaluated on new standard datasets with constrained computational resources. The results showcased significant improvements in search accuracy and efficiency over industry-standard baselines, with notable contributions from both academic and industrial teams. This paper summarizes the competition tracks, datasets, evaluation metrics, and the innovative approaches of the top-performing submissions, providing insights into the current advancements and future directions in the field of approximate nearest neighbor search.

Bridging Dense and Sparse Maximum Inner Product Search

Maximum inner product search (MIPS) over dense and sparse vectors have progressed independently in a bifurcated literature for decades; the latter is better known as top-$k$ retrieval in Information Retrieval. This duality exists because sparse and dense vectors serve different end goals. That is despite the fact that they are manifestations of the same mathematical problem. In this work, we ask if algorithms for dense vectors could be applied effectively to sparse vectors, particularly those that violate the assumptions underlying top-$k$ retrieval methods. We study IVF-based retrieval where vectors are partitioned into clusters and only a fraction of clusters are searched during retrieval. We conduct a comprehensive analysis of dimensionality reduction for sparse vectors, and examine standard and spherical KMeans for partitioning. Our experiments demonstrate that IVF serves as an efficient solution for sparse MIPS. As byproducts, we identify two research opportunities and demonstrate their potential. First, we cast the IVF paradigm as a dynamic pruning technique and turn that insight into a novel organization of the inverted index for approximate MIPS for general sparse vectors. Second, we offer a unified regime for MIPS over vectors that have dense and sparse subspaces, and show its robustness to query distributions.

An Approximate Algorithm for Maximum Inner Product Search over Streaming Sparse Vectors

Maximum Inner Product Search or top-k retrieval on sparse vectors is well-understood in information retrieval, with a number of mature algorithms that solve it exactly. However, all existing algorithms are tailored to text and frequency-based similarity measures. To achieve optimal memory footprint and query latency, they rely on the near stationarity of documents and on laws governing natural languages. We consider, instead, a setup in which collections are streaming -- necessitating dynamic indexing -- and where indexing and retrieval must work with arbitrarily distributed real-valued vectors. As we show, existing algorithms are no longer competitive in this setup, even against naive solutions. We investigate this gap and present a novel approximate solution, called Sinnamon, that can efficiently retrieve the top-k results for sparse real valued vectors drawn from arbitrary distributions. Notably, Sinnamon offers levers to trade-off memory consumption, latency, and accuracy, making the algorithm suitable for constrained applications and systems. We give theoretical results on the error introduced by the approximate nature of the algorithm, and present an empirical evaluation of its performance on two hardware platforms and synthetic and real-valued datasets. We conclude by laying out concrete directions for future research on this general top-k retrieval problem over sparse vectors.

Even Simpler Deterministic Matrix Sketching

This paper provides a one-line proof of Frequent Directions (FD) for sketching streams of matrices. The simpler proof arises from sketching the covariance of the stream of matrices rather than the stream itself.

Streaming Quantiles Algorithms with Small Space and Update Time

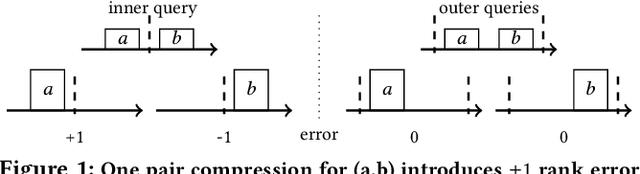
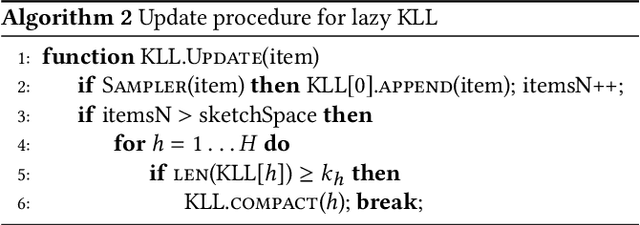
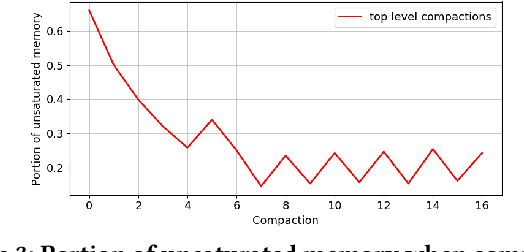
Approximating quantiles and distributions over streaming data has been studied for roughly two decades now. Recently, Karnin, Lang, and Liberty proposed the first asymptotically optimal algorithm for doing so. This manuscript complements their theoretical result by providing a practical variants of their algorithm with improved constants. For a given sketch size, our techniques provably reduce the upper bound on the sketch error by a factor of two. These improvements are verified experimentally. Our modified quantile sketch improves the latency as well by reducing the worst case update time from $O(1/\varepsilon)$ down to $O(\log (1/\varepsilon))$. We also suggest two algorithms for weighted item streams which offer improved asymptotic update times compared to na\"ive extensions. Finally, we provide a specialized data structure for these sketches which reduces both their memory footprints and update times.

Asymmetric Random Projections

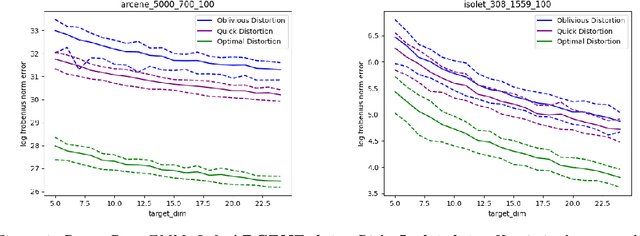
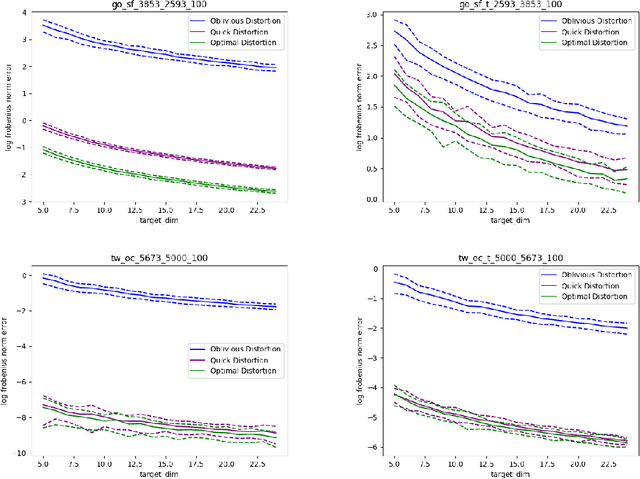
Random projections (RP) are a popular tool for reducing dimensionality while preserving local geometry. In many applications the data set to be projected is given to us in advance, yet the current RP techniques do not make use of information about the data. In this paper, we provide a computationally light way to extract statistics from the data that allows designing a data dependent RP with superior performance compared to data-oblivious RP. We tackle scenarios such as matrix multiplication and linear regression/classification in which we wish to estimate inner products between pairs of vectors from two possibly different sources. Our technique takes advantage of the difference between the sources and is provably superior to oblivious RPs. Additionally, we provide extensive experiments comparing RPs with our approach showing significant performance lifts in fast matrix multiplication, regression and classification problems.

Discrepancy, Coresets, and Sketches in Machine Learning

This paper defines the notion of class discrepancy for families of functions. It shows that low discrepancy classes admit small offline and streaming coresets. We provide general techniques for bounding the class discrepancy of machine learning problems. As corollaries of the general technique we bound the discrepancy (and therefore coreset complexity) of logistic regression, sigmoid activation loss, matrix covariance, kernel density and any analytic function of the dot product or the squared distance. Our results prove the existence of epsilon-approximation O(sqrt{d}/epsilon) sized coresets for the above problems. This resolves the long-standing open problem regarding the coreset complexity of Gaussian kernel density estimation. We provide two more related but independent results. First, an exponential improvement of the widely used merge-and-reduce trick which gives improved streaming sketches for any low discrepancy problem. Second, an extremely simple deterministic algorithm for finding low discrepancy sequences (and therefore coresets) for any positive semi-definite kernel. This paper establishes some explicit connections between class discrepancy, coreset complexity, learnability, and streaming algorithms.

ProxQuant: Quantized Neural Networks via Proximal Operators

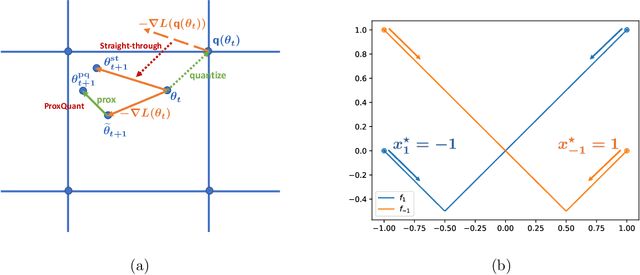
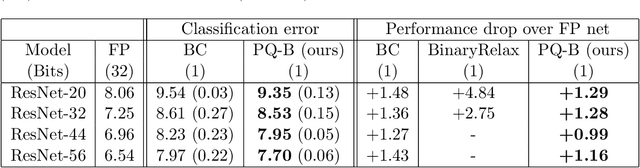
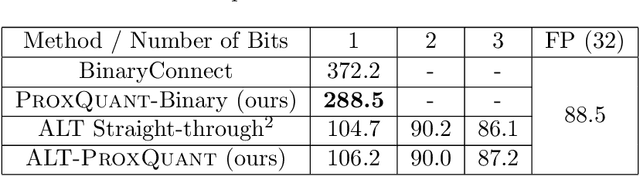
To make deep neural networks feasible in resource-constrained environments (such as mobile devices), it is beneficial to quantize models by using low-precision weights. One common technique for quantizing neural networks is the straight-through gradient method, which enables back-propagation through the quantization mapping. Despite its empirical success, little is understood about why the straight-through gradient method works. Building upon a novel observation that the straight-through gradient method is in fact identical to the well-known Nesterov's dual-averaging algorithm on a quantization constrained optimization problem, we propose a more principled alternative approach, called ProxQuant, that formulates quantized network training as a regularized learning problem instead and optimizes it via the prox-gradient method. ProxQuant does back-propagation on the underlying full-precision vector and applies an efficient prox-operator in between stochastic gradient steps to encourage quantizedness. For quantizing ResNets and LSTMs, ProxQuant outperforms state-of-the-art results on binary quantization and is on par with state-of-the-art on multi-bit quantization. For binary quantization, our analysis shows both theoretically and experimentally that ProxQuant is more stable than the straight-through gradient method (i.e. BinaryConnect), challenging the indispensability of the straight-through gradient method and providing a powerful alternative.

An Algorithm for Online K-Means Clustering

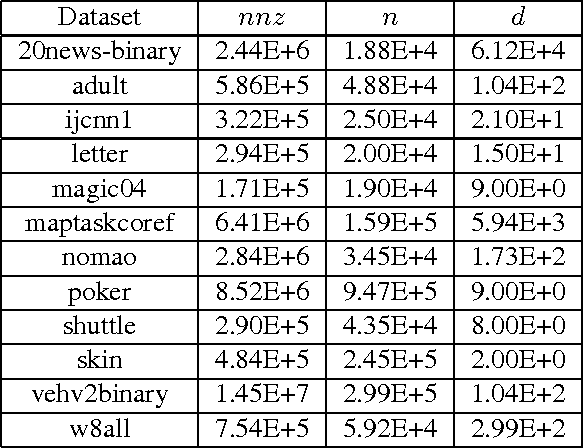
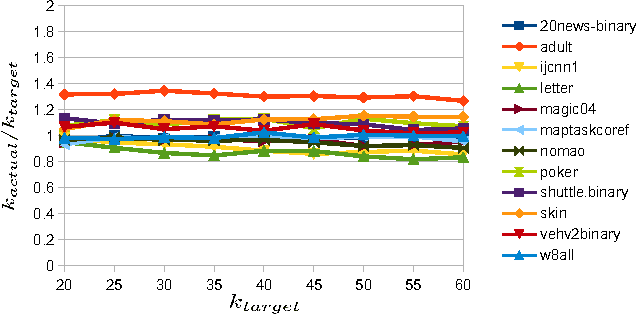
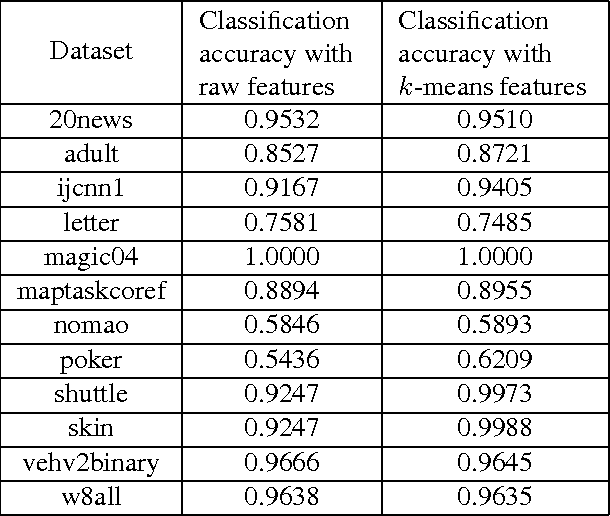
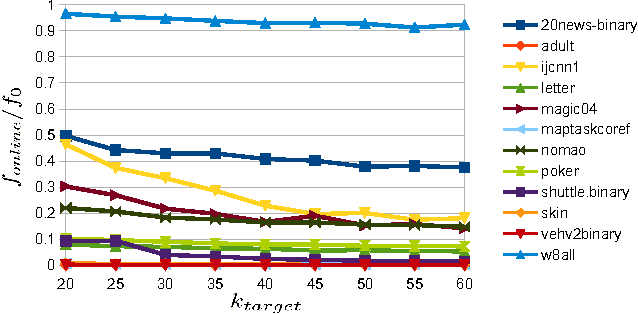
This paper shows that one can be competitive with the k-means objective while operating online. In this model, the algorithm receives vectors v_1,...,v_n one by one in an arbitrary order. For each vector the algorithm outputs a cluster identifier before receiving the next one. Our online algorithm generates ~O(k) clusters whose k-means cost is ~O(W*). Here, W* is the optimal k-means cost using k clusters and ~O suppresses poly-logarithmic factors. We also show that, experimentally, it is not much worse than k-means++ while operating in a strictly more constrained computational model.

Near-Optimal Entrywise Sampling for Data Matrices

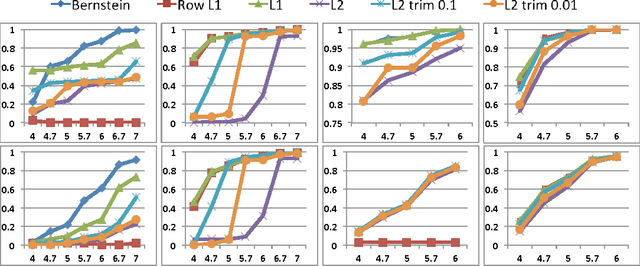
We consider the problem of selecting non-zero entries of a matrix $A$ in order to produce a sparse sketch of it, $B$, that minimizes $\|A-B\|_2$. For large $m \times n$ matrices, such that $n \gg m$ (for example, representing $n$ observations over $m$ attributes) we give sampling distributions that exhibit four important properties. First, they have closed forms computable from minimal information regarding $A$. Second, they allow sketching of matrices whose non-zeros are presented to the algorithm in arbitrary order as a stream, with $O(1)$ computation per non-zero. Third, the resulting sketch matrices are not only sparse, but their non-zero entries are highly compressible. Lastly, and most importantly, under mild assumptions, our distributions are provably competitive with the optimal offline distribution. Note that the probabilities in the optimal offline distribution may be complex functions of all the entries in the matrix. Therefore, regardless of computational complexity, the optimal distribution might be impossible to compute in the streaming model.