Results of the Big ANN: NeurIPS'23 competition

The 2023 Big ANN Challenge, held at NeurIPS 2023, focused on advancing the state-of-the-art in indexing data structures and search algorithms for practical variants of Approximate Nearest Neighbor (ANN) search that reflect the growing complexity and diversity of workloads. Unlike prior challenges that emphasized scaling up classical ANN search ~\cite{DBLP:conf/nips/SimhadriWADBBCH21}, this competition addressed filtered search, out-of-distribution data, sparse and streaming variants of ANNS. Participants developed and submitted innovative solutions that were evaluated on new standard datasets with constrained computational resources. The results showcased significant improvements in search accuracy and efficiency over industry-standard baselines, with notable contributions from both academic and industrial teams. This paper summarizes the competition tracks, datasets, evaluation metrics, and the innovative approaches of the top-performing submissions, providing insights into the current advancements and future directions in the field of approximate nearest neighbor search.

PLAN: Variance-Aware Private Mean Estimation

Differentially private mean estimation is an important building block in privacy-preserving algorithms for data analysis and machine learning. Though the trade-off between privacy and utility is well understood in the worst case, many datasets exhibit structure that could potentially be exploited to yield better algorithms. In this paper we present $\textit{Private Limit Adapted Noise}$ (PLAN), a family of differentially private algorithms for mean estimation in the setting where inputs are independently sampled from a distribution $\mathcal{D}$ over $\mathbf{R}^d$, with coordinate-wise standard deviations $\boldsymbol{\sigma} \in \mathbf{R}^d$. Similar to mean estimation under Mahalanobis distance, PLAN tailors the shape of the noise to the shape of the data, but unlike previous algorithms the privacy budget is spent non-uniformly over the coordinates. Under a concentration assumption on $\mathcal{D}$, we show how to exploit skew in the vector $\boldsymbol{\sigma}$, obtaining a (zero-concentrated) differentially private mean estimate with $\ell_2$ error proportional to $\|\boldsymbol{\sigma}\|_1$. Previous work has either not taken $\boldsymbol{\sigma}$ into account, or measured error in Mahalanobis distance $\unicode{x2013}$ in both cases resulting in $\ell_2$ error proportional to $\sqrt{d}\|\boldsymbol{\sigma}\|_2$, which can be up to a factor $\sqrt{d}$ larger. To verify the effectiveness of PLAN, we empirically evaluate accuracy on both synthetic and real world data.

Results of the NeurIPS'21 Challenge on Billion-Scale Approximate Nearest Neighbor Search

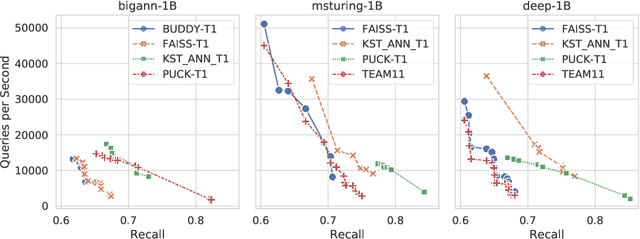
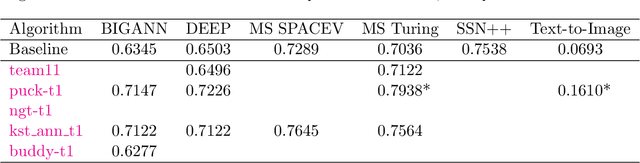
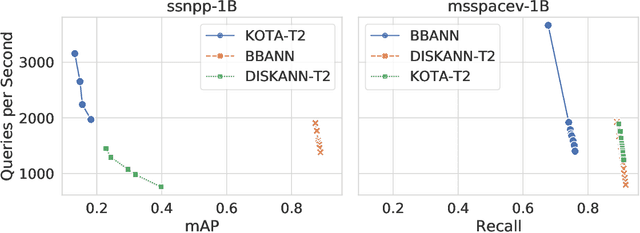
Despite the broad range of algorithms for Approximate Nearest Neighbor Search, most empirical evaluations of algorithms have focused on smaller datasets, typically of 1 million points~\citep{Benchmark}. However, deploying recent advances in embedding based techniques for search, recommendation and ranking at scale require ANNS indices at billion, trillion or larger scale. Barring a few recent papers, there is limited consensus on which algorithms are effective at this scale vis-\`a-vis their hardware cost. This competition compares ANNS algorithms at billion-scale by hardware cost, accuracy and performance. We set up an open source evaluation framework and leaderboards for both standardized and specialized hardware. The competition involves three tracks. The standard hardware track T1 evaluates algorithms on an Azure VM with limited DRAM, often the bottleneck in serving billion-scale indices, where the embedding data can be hundreds of GigaBytes in size. It uses FAISS~\citep{Faiss17} as the baseline. The standard hardware track T2 additional allows inexpensive SSDs in addition to the limited DRAM and uses DiskANN~\citep{DiskANN19} as the baseline. The specialized hardware track T3 allows any hardware configuration, and again uses FAISS as the baseline. We compiled six diverse billion-scale datasets, four newly released for this competition, that span a variety of modalities, data types, dimensions, deep learning models, distance functions and sources. The outcome of the competition was ranked leaderboards of algorithms in each track based on recall at a query throughput threshold. Additionally, for track T3, separate leaderboards were created based on recall as well as cost-normalized and power-normalized query throughput.

DEANN: Speeding up Kernel-Density Estimation using Approximate Nearest Neighbor Search

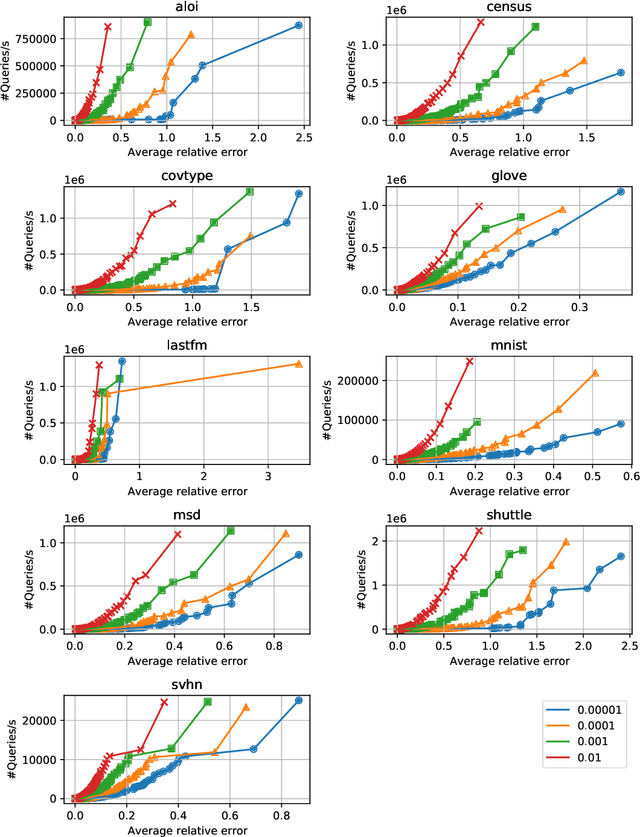
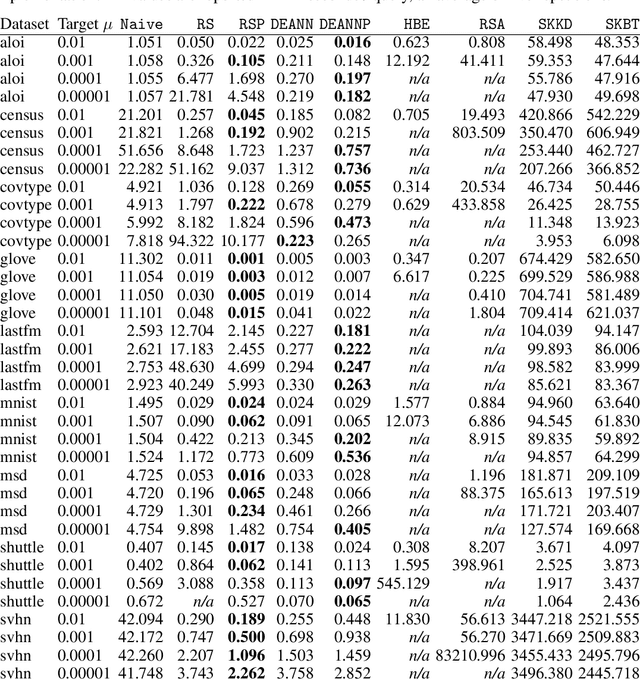
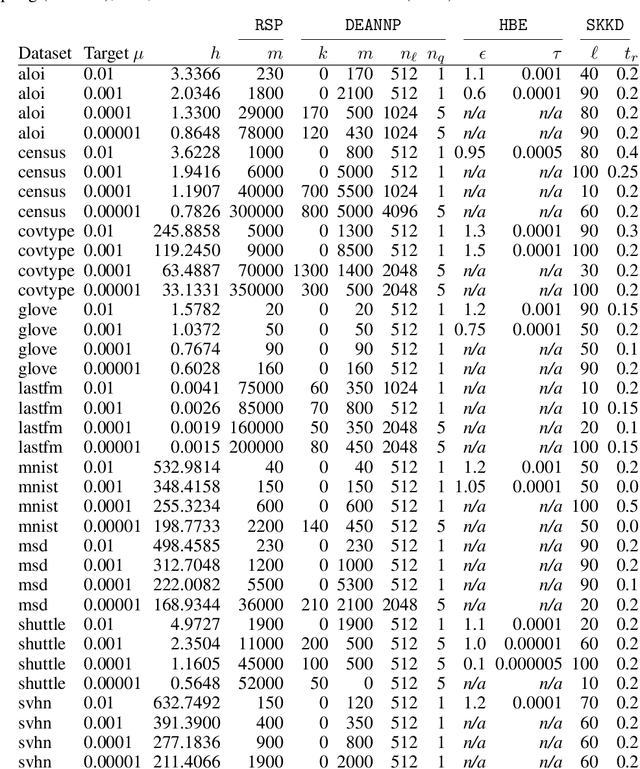
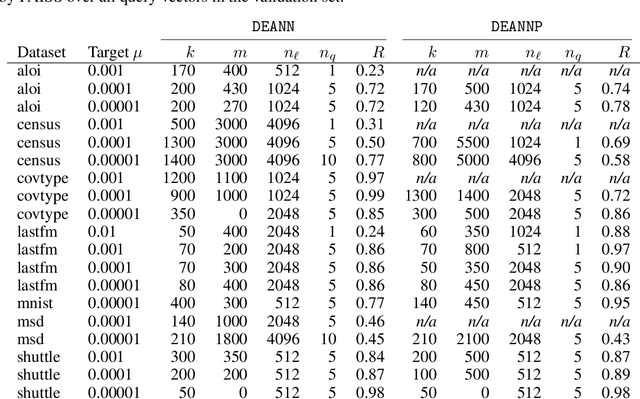
Kernel Density Estimation (KDE) is a nonparametric method for estimating the shape of a density function, given a set of samples from the distribution. Recently, locality-sensitive hashing, originally proposed as a tool for nearest neighbor search, has been shown to enable fast KDE data structures. However, these approaches do not take advantage of the many other advances that have been made in algorithms for nearest neighbor algorithms. We present an algorithm called Density Estimation from Approximate Nearest Neighbors (DEANN) where we apply Approximate Nearest Neighbor (ANN) algorithms as a black box subroutine to compute an unbiased KDE. The idea is to find points that have a large contribution to the KDE using ANN, compute their contribution exactly, and approximate the remainder with Random Sampling (RS). We present a theoretical argument that supports the idea that an ANN subroutine can speed up the evaluation. Furthermore, we provide a C++ implementation with a Python interface that can make use of an arbitrary ANN implementation as a subroutine for KDE evaluation. We show empirically that our implementation outperforms state of the art implementations in all high dimensional datasets we considered, and matches the performance of RS in cases where the ANN yield no gains in performance.

Sampling a Near Neighbor in High Dimensions -- Who is the Fairest of Them All?

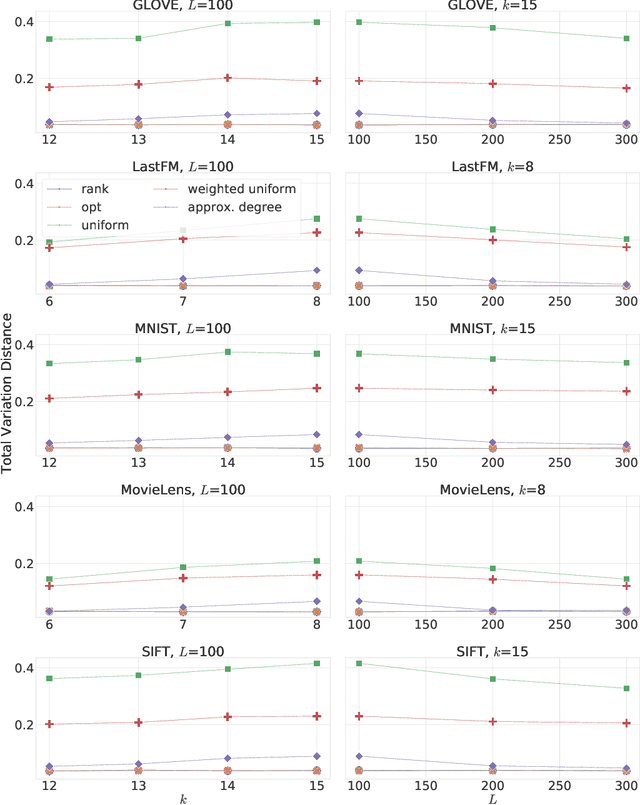
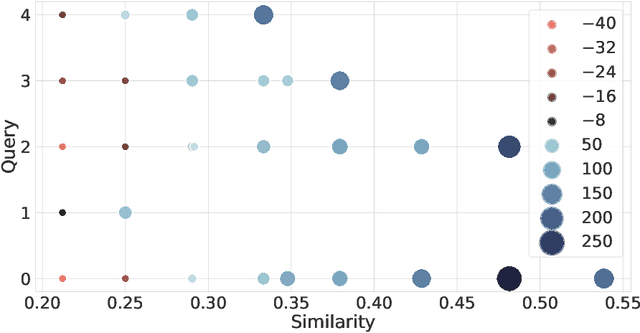
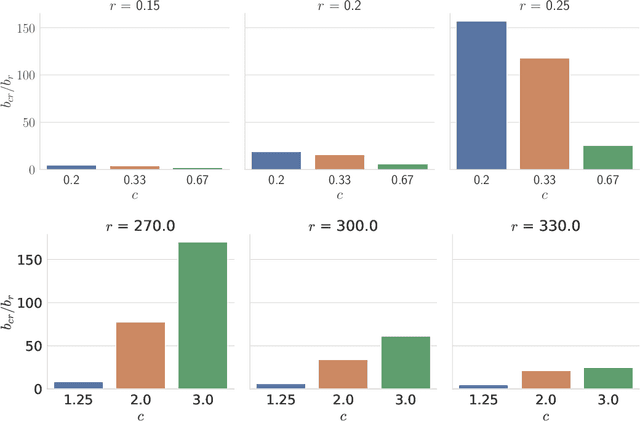
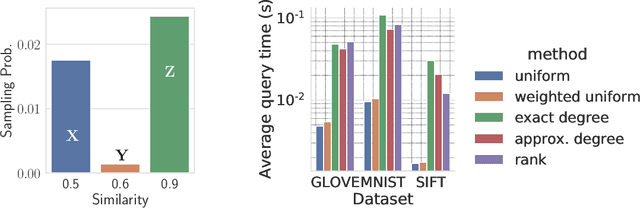
Similarity search is a fundamental algorithmic primitive, widely used in many computer science disciplines. Given a set of points $S$ and a radius parameter $r>0$, the $r$-near neighbor ($r$-NN) problem asks for a data structure that, given any query point $q$, returns a point $p$ within distance at most $r$ from $q$. In this paper, we study the $r$-NN problem in the light of individual fairness and providing equal opportunities: all points that are within distance $r$ from the query should have the same probability to be returned. In the low-dimensional case, this problem was first studied by Hu, Qiao, and Tao (PODS 2014). Locality sensitive hashing (LSH), the theoretically strongest approach to similarity search in high dimensions, does not provide such a fairness guarantee. In this work, we show that LSH based algorithms can be made fair, without a significant loss in efficiency. We propose several efficient data structures for the exact and approximate variants of the fair NN problem. Our approach works more generally for sampling uniformly from a sub-collection of sets of a given collection and can be used in a few other applications. We also develop a data structure for fair similarity search under inner product that requires nearly-linear space and exploits locality sensitive filters. The paper concludes with an experimental evaluation that highlights the inherent unfairness of NN data structures and shows the performance of our algorithms on real-world datasets.

Differentially Private Sketches for Jaccard Similarity Estimation

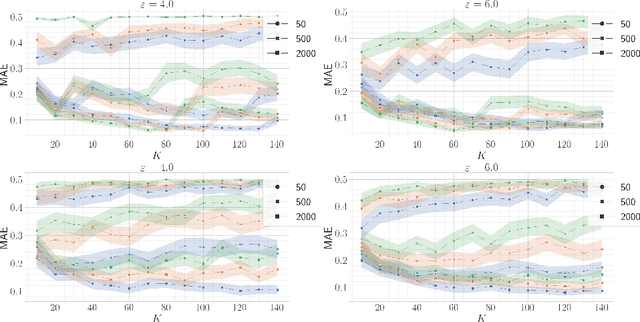
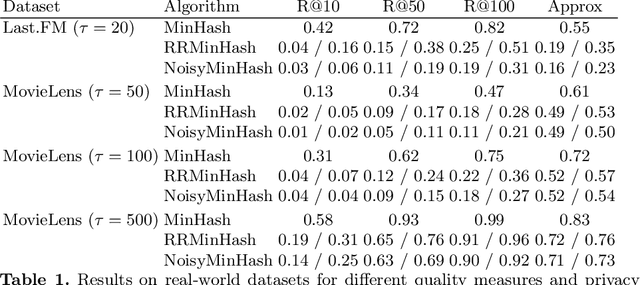
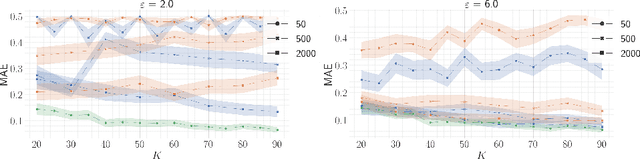
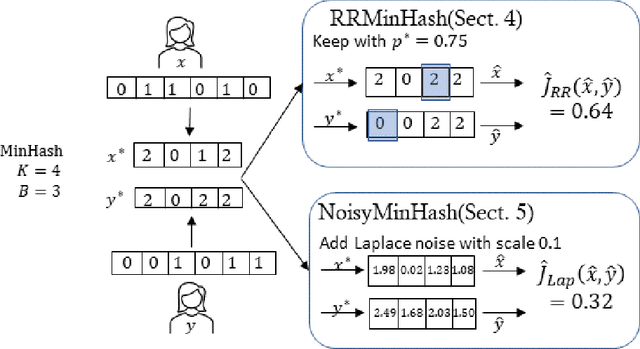
This paper describes two locally-differential private algorithms for releasing user vectors such that the Jaccard similarity between these vectors can be efficiently estimated. The basic building block is the well known MinHash method. To achieve a privacy-utility trade-off, MinHash is extended in two ways using variants of Generalized Randomized Response and the Laplace Mechanism. A theoretical analysis provides bounds on the absolute error and experiments show the utility-privacy trade-off on synthetic and real-world data. The paper ends with a critical discussion of related work.

Fair Near Neighbor Search: Independent Range Sampling in High Dimensions

Similarity search is a fundamental algorithmic primitive, widely used in many computer science disciplines. There are several variants of the similarity search problem, and one of the most relevant is the $r$-near neighbor ($r$-NN) problem: given a radius $r>0$ and a set of points $S$, construct a data structure that, for any given query point $q$, returns a point $p$ within distance at most $r$ from $q$. In this paper, we study the $r$-NN problem in the light of fairness. We consider fairness in the sense of equal opportunity: all points that are within distance $r$ from the query should have the same probability to be returned. Locality sensitive hashing (LSH), the most common approach to similarity search in high dimensions, does not provide such a fairness guarantee. To address this, we propose efficient data structures for $r$-NN where all points in $S$ that are near $q$ have the same probability to be selected and returned by the query. Specifically, we first propose a black-box approach that, given any LSH scheme, constructs a data structure for uniformly sampling points in the neighborhood of a query. Then, we develop a data structure for fair similarity search under inner product, which requires nearly-linear space and exploits locality sensitive filters.