John Hopcroft
Adversarially Robust Generalization Just Requires More Unlabeled Data
Jun 03, 2019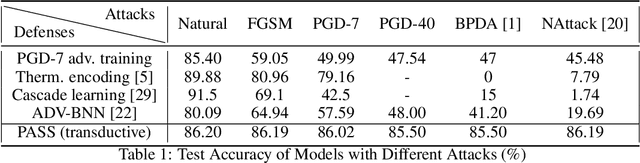
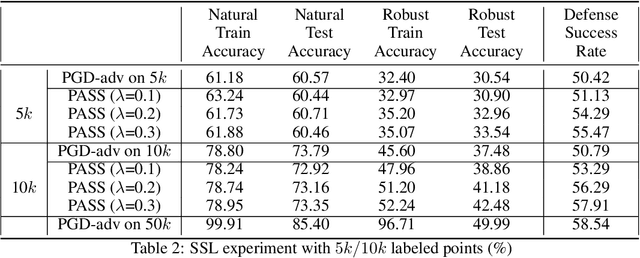
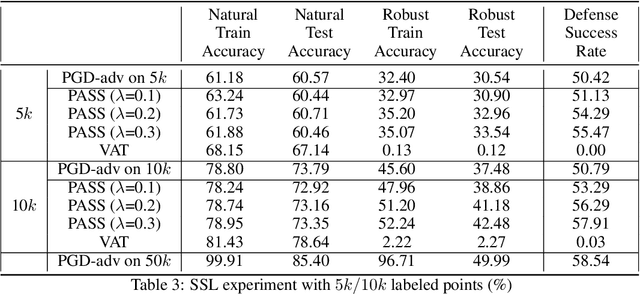
Abstract:Neural network robustness has recently been highlighted by the existence of adversarial examples. Many previous works show that the learned networks do not perform well on perturbed test data, and significantly more labeled data is required to achieve adversarially robust generalization. In this paper, we theoretically and empirically show that with just more unlabeled data, we can learn a model with better adversarially robust generalization. The key insight of our results is based on a risk decomposition theorem, in which the expected robust risk is separated into two parts: the stability part which measures the prediction stability in the presence of perturbations, and the accuracy part which evaluates the standard classification accuracy. As the stability part does not depend on any label information, we can optimize this part using unlabeled data. We further prove that for a specific Gaussian mixture problem illustrated by \cite{schmidt2018adversarially}, adversarially robust generalization can be almost as easy as the standard generalization in supervised learning if a sufficiently large amount of unlabeled data is provided. Inspired by the theoretical findings, we propose a new algorithm called PASS by leveraging unlabeled data during adversarial training. We show that in the transductive and semi-supervised settings, PASS achieves higher robust accuracy and defense success rate on the Cifar-10 task.
Towards Understanding Learning Representations: To What Extent Do Different Neural Networks Learn the Same Representation
Oct 28, 2018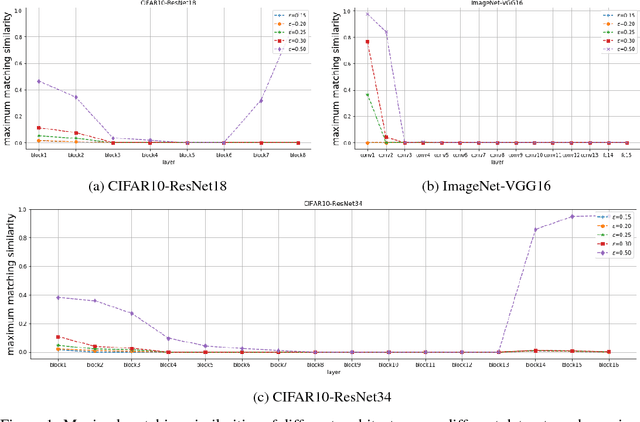


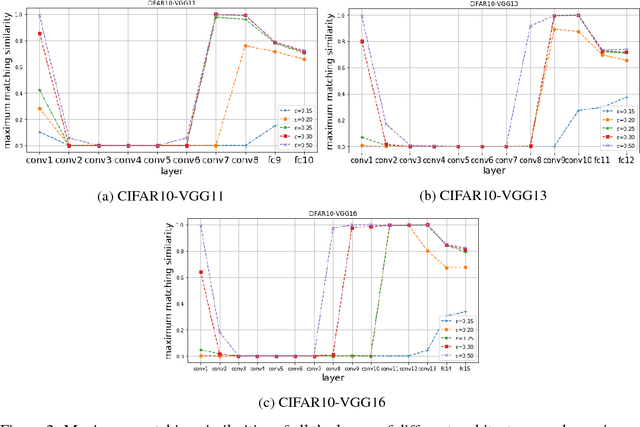
Abstract:It is widely believed that learning good representations is one of the main reasons for the success of deep neural networks. Although highly intuitive, there is a lack of theory and systematic approach quantitatively characterizing what representations do deep neural networks learn. In this work, we move a tiny step towards a theory and better understanding of the representations. Specifically, we study a simpler problem: How similar are the representations learned by two networks with identical architecture but trained from different initializations. We develop a rigorous theory based on the neuron activation subspace match model. The theory gives a complete characterization of the structure of neuron activation subspace matches, where the core concepts are maximum match and simple match which describe the overall and the finest similarity between sets of neurons in two networks respectively. We also propose efficient algorithms to find the maximum match and simple matches. Finally, we conduct extensive experiments using our algorithms. Experimental results suggest that, surprisingly, representations learned by the same convolutional layers of networks trained from different initializations are not as similar as prevalently expected, at least in terms of subspace match.
Stacked Generative Adversarial Networks
Apr 12, 2017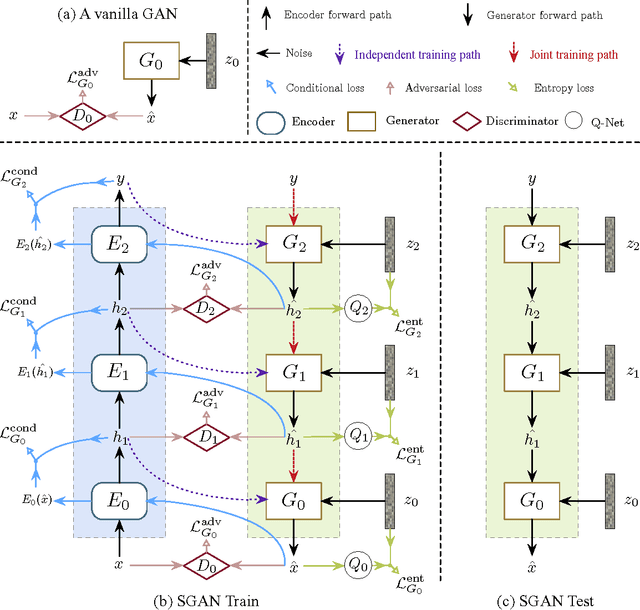
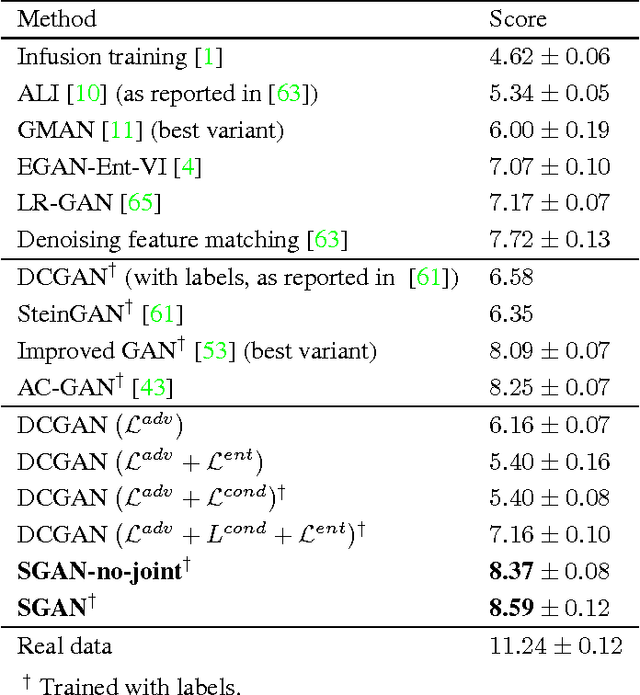


Abstract:In this paper, we propose a novel generative model named Stacked Generative Adversarial Networks (SGAN), which is trained to invert the hierarchical representations of a bottom-up discriminative network. Our model consists of a top-down stack of GANs, each learned to generate lower-level representations conditioned on higher-level representations. A representation discriminator is introduced at each feature hierarchy to encourage the representation manifold of the generator to align with that of the bottom-up discriminative network, leveraging the powerful discriminative representations to guide the generative model. In addition, we introduce a conditional loss that encourages the use of conditional information from the layer above, and a novel entropy loss that maximizes a variational lower bound on the conditional entropy of generator outputs. We first train each stack independently, and then train the whole model end-to-end. Unlike the original GAN that uses a single noise vector to represent all the variations, our SGAN decomposes variations into multiple levels and gradually resolves uncertainties in the top-down generative process. Based on visual inspection, Inception scores and visual Turing test, we demonstrate that SGAN is able to generate images of much higher quality than GANs without stacking.
A Powerful Generative Model Using Random Weights for the Deep Image Representation
Jun 16, 2016

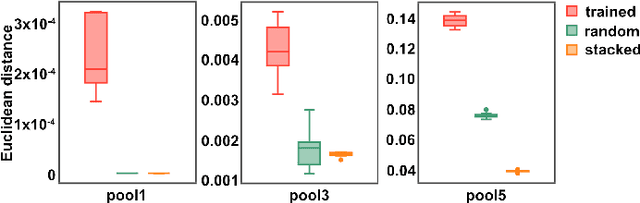

Abstract:To what extent is the success of deep visualization due to the training? Could we do deep visualization using untrained, random weight networks? To address this issue, we explore new and powerful generative models for three popular deep visualization tasks using untrained, random weight convolutional neural networks. First we invert representations in feature spaces and reconstruct images from white noise inputs. The reconstruction quality is statistically higher than that of the same method applied on well trained networks with the same architecture. Next we synthesize textures using scaled correlations of representations in multiple layers and our results are almost indistinguishable with the original natural texture and the synthesized textures based on the trained network. Third, by recasting the content of an image in the style of various artworks, we create artistic images with high perceptual quality, highly competitive to the prior work of Gatys et al. on pretrained networks. To our knowledge this is the first demonstration of image representations using untrained deep neural networks. Our work provides a new and fascinating tool to study the representation of deep network architecture and sheds light on new understandings on deep visualization.
Convergent Learning: Do different neural networks learn the same representations?
Feb 28, 2016
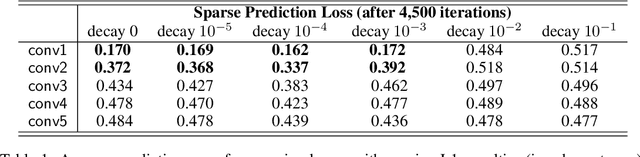

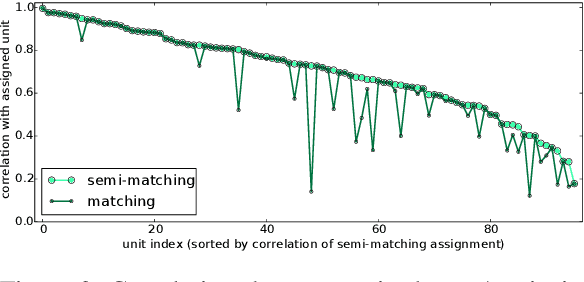
Abstract:Recent success in training deep neural networks have prompted active investigation into the features learned on their intermediate layers. Such research is difficult because it requires making sense of non-linear computations performed by millions of parameters, but valuable because it increases our ability to understand current models and create improved versions of them. In this paper we investigate the extent to which neural networks exhibit what we call convergent learning, which is when the representations learned by multiple nets converge to a set of features which are either individually similar between networks or where subsets of features span similar low-dimensional spaces. We propose a specific method of probing representations: training multiple networks and then comparing and contrasting their individual, learned representations at the level of neurons or groups of neurons. We begin research into this question using three techniques to approximately align different neural networks on a feature level: a bipartite matching approach that makes one-to-one assignments between neurons, a sparse prediction approach that finds one-to-many mappings, and a spectral clustering approach that finds many-to-many mappings. This initial investigation reveals a few previously unknown properties of neural networks, and we argue that future research into the question of convergent learning will yield many more. The insights described here include (1) that some features are learned reliably in multiple networks, yet other features are not consistently learned; (2) that units learn to span low-dimensional subspaces and, while these subspaces are common to multiple networks, the specific basis vectors learned are not; (3) that the representation codes show evidence of being a mix between a local code and slightly, but not fully, distributed codes across multiple units.
Sign Stable Projections, Sign Cauchy Projections and Chi-Square Kernels
Aug 05, 2013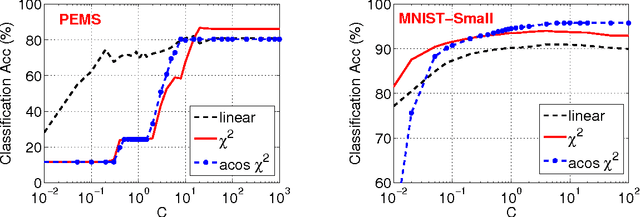
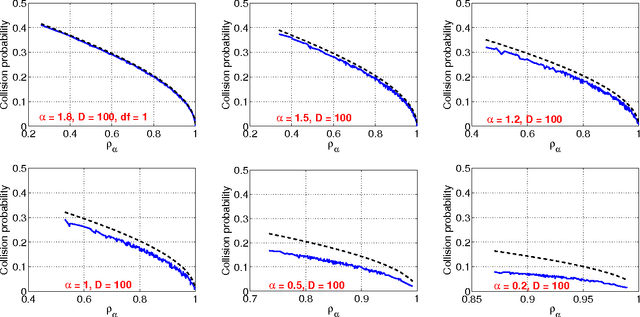
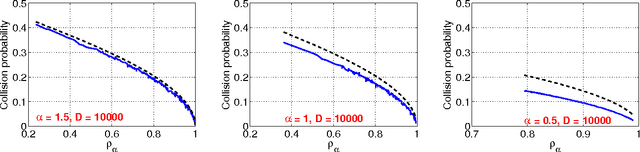
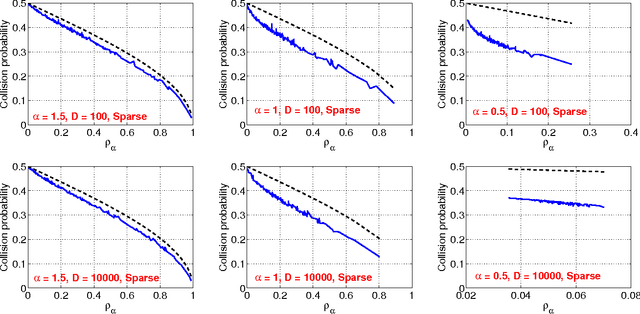
Abstract:The method of stable random projections is popular for efficiently computing the Lp distances in high dimension (where 0<p<=2), using small space. Because it adopts nonadaptive linear projections, this method is naturally suitable when the data are collected in a dynamic streaming fashion (i.e., turnstile data streams). In this paper, we propose to use only the signs of the projected data and analyze the probability of collision (i.e., when the two signs differ). We derive a bound of the collision probability which is exact when p=2 and becomes less sharp when p moves away from 2. Interestingly, when p=1 (i.e., Cauchy random projections), we show that the probability of collision can be accurately approximated as functions of the chi-square similarity. For example, when the (un-normalized) data are binary, the maximum approximation error of the collision probability is smaller than 0.0192. In text and vision applications, the chi-square similarity is a popular measure for nonnegative data when the features are generated from histograms. Our experiments confirm that the proposed method is promising for large-scale learning applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge