A Hybrid Autoencoder-Transformer Model for Robust Day-Ahead Electricity Price Forecasting under Extreme Conditions

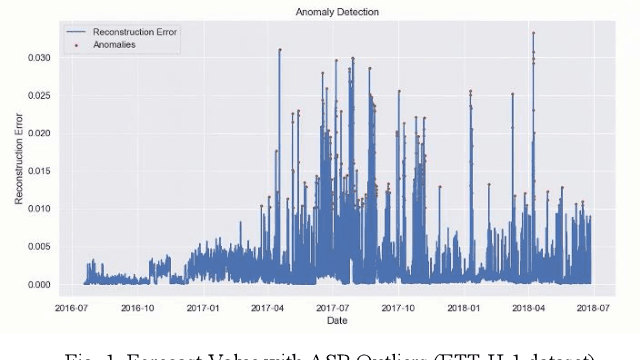
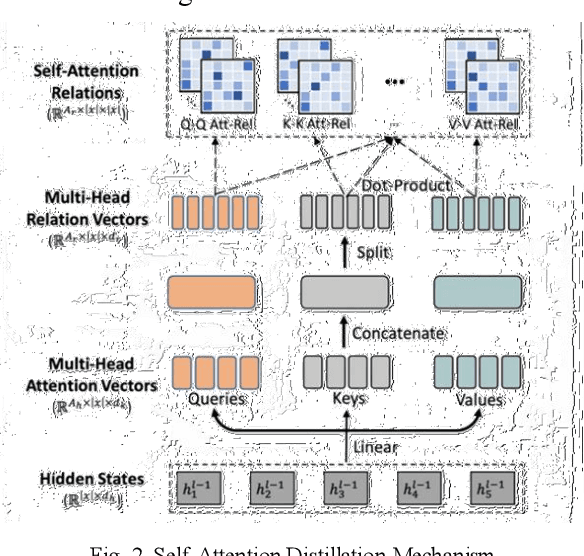
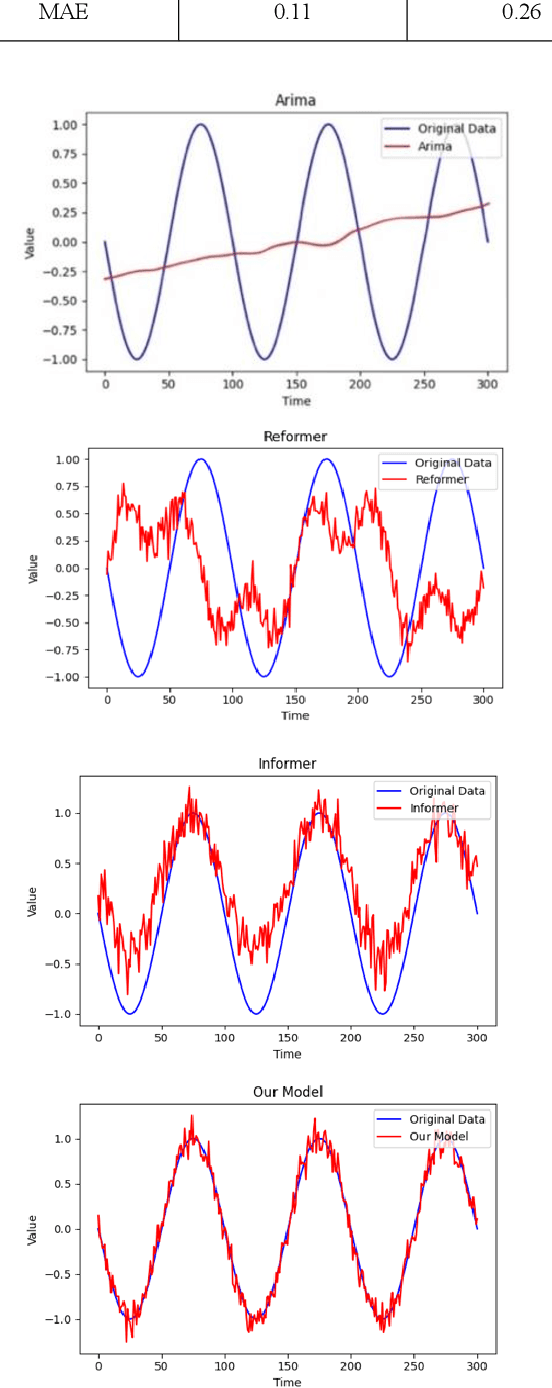
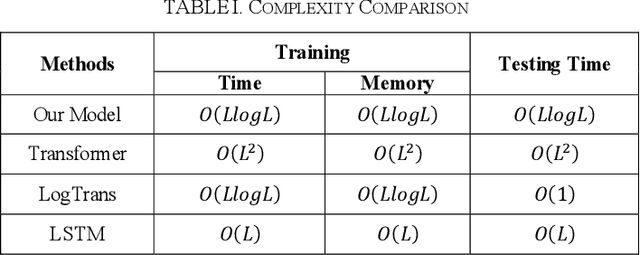
Accurate day-ahead electricity price forecasting (DAEPF) is critical for the efficient operation of power systems, but extreme condition and market anomalies pose significant challenges to existing forecasting methods. To overcome these challenges, this paper proposes a novel hybrid deep learning framework that integrates a Distilled Attention Transformer (DAT) model and an Autoencoder Self-regression Model (ASM). The DAT leverages a self-attention mechanism to dynamically assign higher weights to critical segments of historical data, effectively capturing both long-term trends and short-term fluctuations. Concurrently, the ASM employs unsupervised learning to detect and isolate anomalous patterns induced by extreme conditions, such as heavy rain, heat waves, or human festivals. Experiments on datasets sampled from California and Shandong Province demonstrate that our framework significantly outperforms state-of-the-art methods in prediction accuracy, robustness, and computational efficiency. Our framework thus holds promise for enhancing grid resilience and optimizing market operations in future power systems.

COTN: A Chaotic Oscillatory Transformer Network for Complex Volatile Systems under Extreme Conditions

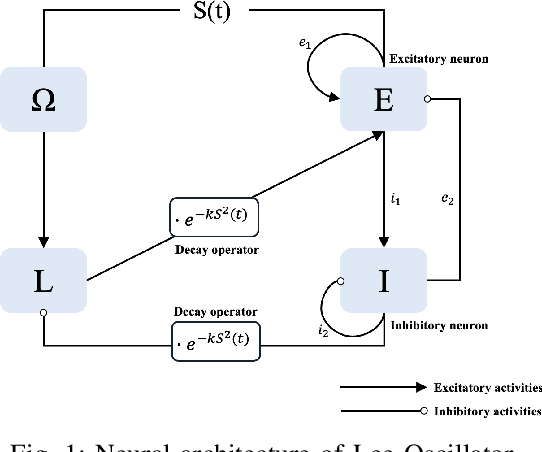
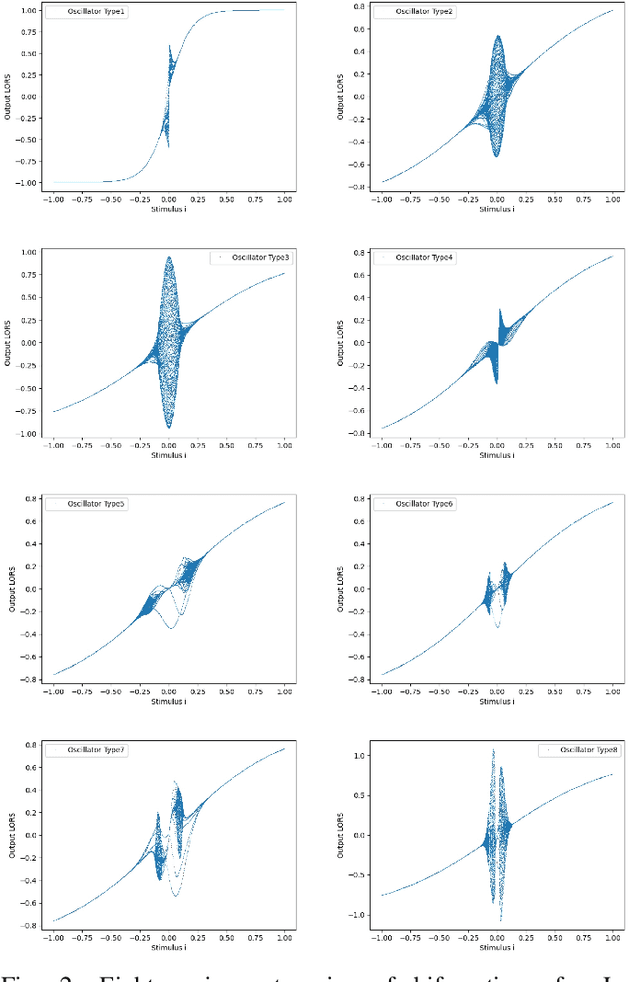
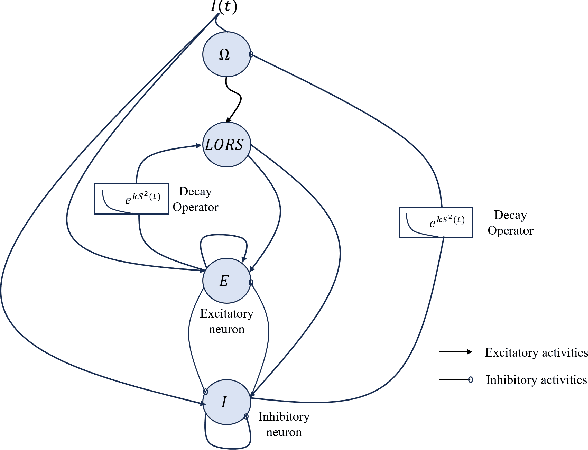
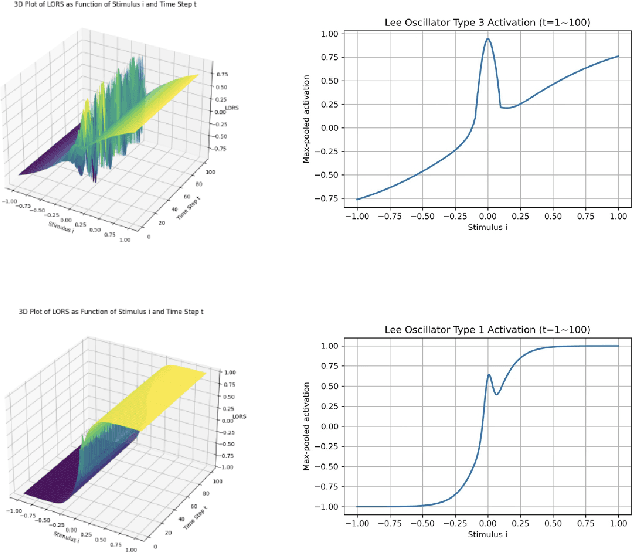
Accurate prediction of financial and electricity markets, especially under extreme conditions, remains a significant challenge due to their intrinsic nonlinearity, rapid fluctuations, and chaotic patterns. To address these limitations, we propose the Chaotic Oscillatory Transformer Network (COTN). COTN innovatively combines a Transformer architecture with a novel Lee Oscillator activation function, processed through Max-over-Time pooling and a lambda-gating mechanism. This design is specifically tailored to effectively capture chaotic dynamics and improve responsiveness during periods of heightened volatility, where conventional activation functions (e.g., ReLU, GELU) tend to saturate. Furthermore, COTN incorporates an Autoencoder Self-Regressive (ASR) module to detect and isolate abnormal market patterns, such as sudden price spikes or crashes, thereby preventing corruption of the core prediction process and enhancing robustness. Extensive experiments across electricity spot markets and financial markets demonstrate the practical applicability and resilience of COTN. Our approach outperforms state-of-the-art deep learning models like Informer by up to 17% and traditional statistical methods like GARCH by as much as 40%. These results underscore COTN's effectiveness in navigating real-world market uncertainty and complexity, offering a powerful tool for forecasting highly volatile systems under duress.

When GNNs meet symmetry in ILPs: an orbit-based feature augmentation approach

A common characteristic in integer linear programs (ILPs) is symmetry, allowing variables to be permuted without altering the underlying problem structure. Recently, GNNs have emerged as a promising approach for solving ILPs. However, a significant challenge arises when applying GNNs to ILPs with symmetry: classic GNN architectures struggle to differentiate between symmetric variables, which limits their predictive accuracy. In this work, we investigate the properties of permutation equivariance and invariance in GNNs, particularly in relation to the inherent symmetry of ILP formulations. We reveal that the interaction between these two factors contributes to the difficulty of distinguishing between symmetric variables. To address this challenge, we explore the potential of feature augmentation and propose several guiding principles for constructing augmented features. Building on these principles, we develop an orbit-based augmentation scheme that first groups symmetric variables and then samples augmented features for each group from a discrete uniform distribution. Empirical results demonstrate that our proposed approach significantly enhances both training efficiency and predictive performance.

An Efficient Unsupervised Framework for Convex Quadratic Programs via Deep Unrolling

Quadratic programs (QPs) arise in various domains such as machine learning, finance, and control. Recently, learning-enhanced primal-dual hybrid gradient (PDHG) methods have shown great potential in addressing large-scale linear programs; however, this approach has not been extended to QPs. In this work, we focus on unrolling "PDQP", a PDHG algorithm specialized for convex QPs. Specifically, we propose a neural network model called "PDQP-net" to learn optimal QP solutions. Theoretically, we demonstrate that a PDQP-net of polynomial size can align with the PDQP algorithm, returning optimal primal-dual solution pairs. We propose an unsupervised method that incorporates KKT conditions into the loss function. Unlike the standard learning-to-optimize framework that requires optimization solutions generated by solvers, our unsupervised method adjusts the network weights directly from the evaluation of the primal-dual gap. This method has two benefits over supervised learning: first, it helps generate better primal-dual gap since the primal-dual gap is in the objective function; second, it does not require solvers. We show that PDQP-net trained in this unsupervised manner can effectively approximate optimal QP solutions. Extensive numerical experiments confirm our findings, indicating that using PDQP-net predictions to warm-start PDQP can achieve up to 45% acceleration on QP instances. Moreover, it achieves 14% to 31% acceleration on out-of-distribution instances.

Invar-RAG: Invariant LLM-aligned Retrieval for Better Generation

Retrieval-augmented generation (RAG) has shown impressive capability in providing reliable answer predictions and addressing hallucination problems. A typical RAG implementation uses powerful retrieval models to extract external information and large language models (LLMs) to generate answers. In contrast, recent LLM-based retrieval has gained attention for its substantial improvements in information retrieval (IR) due to the LLMs' semantic understanding capability. However, directly applying LLM to RAG systems presents challenges. This may cause feature locality problems as massive parametric knowledge can hinder effective usage of global information across the corpus; for example, an LLM-based retriever often inputs document summaries instead of full documents. Moreover, various pre-trained tasks in LLMs introduce variance, further weakening performance as a retriever. To address these issues, we propose a novel two-stage fine-tuning architecture called Invar-RAG. In the retrieval stage, an LLM-based retriever is constructed by integrating LoRA-based representation learning to tackle feature locality issues. To enhance retrieval performance, we develop two patterns (invariant and variant patterns) and an invariance loss to reduce LLM variance. In the generation stage, a refined fine-tuning method is employed to improve LLM accuracy in generating answers based on retrieved information. Experimental results show that Invar-RAG significantly outperforms existing baselines across three open-domain question answering (ODQA) datasets. Code is available in the Supplementary Material for reproducibility.