Fast localization and single-pixel imaging of the moving object using time-division multiplexing

When imaging moving objects, single-pixel imaging produces motion blur. This paper proposes a new single-pixel imaging method, which can achieve anti-motion blur imaging of a fast-moving object. The geometric moment patterns and Hadamard patterns are used to alternately encode the position information and the image information of the object with time-division multiplexing. In the reconstruction process, the object position information is extracted independently and combining motion-compensation reconstruction algorithm to decouple the object motion from image information. As a result, the anti-motion blur image and the high frame rate object positions are obtained. Experimental results show that for a moving object with an angular velocity of up to 0.5rad/s relative to the imaging system, the proposed method achieves a localization frequency of 5.55kHz, and gradually reconstructs a clear image of the fast-moving object with a pseudo resolution of 512x512. The method has application prospects in single-pixel imaging of the fast-moving object.

Deep Sufficient Representation Learning via Mutual Information

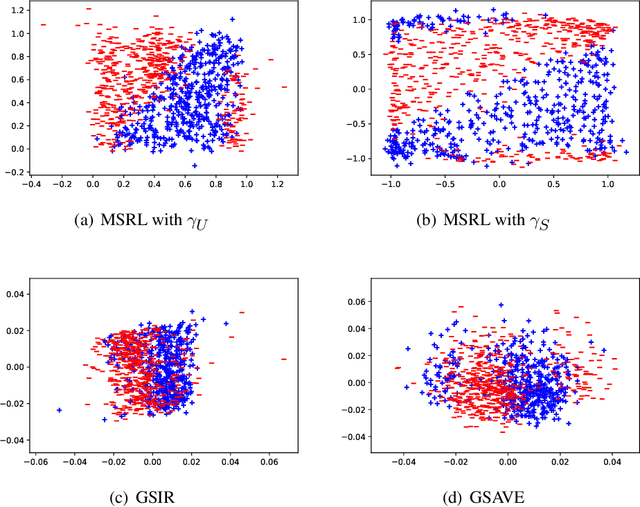
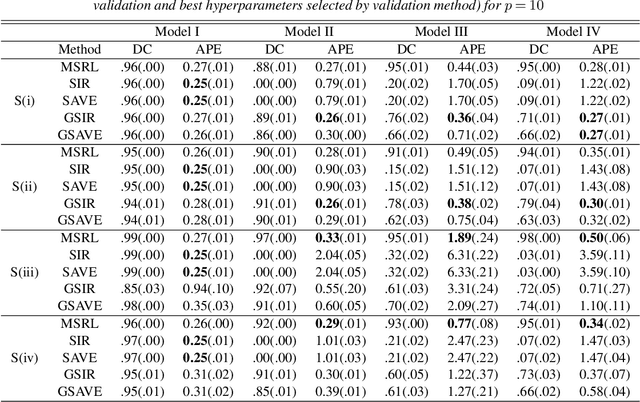
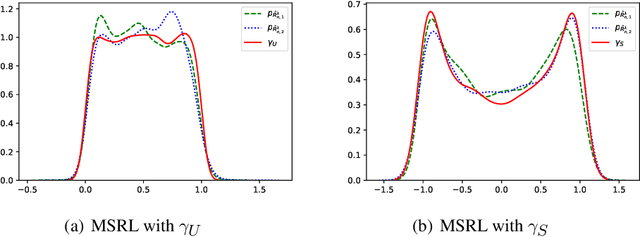
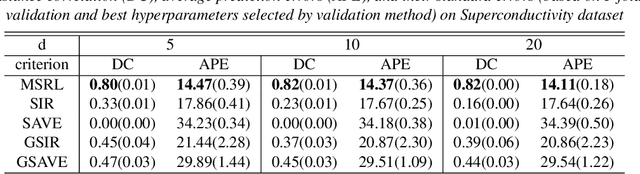
We propose a mutual information-based sufficient representation learning (MSRL) approach, which uses the variational formulation of the mutual information and leverages the approximation power of deep neural networks. MSRL learns a sufficient representation with the maximum mutual information with the response and a user-selected distribution. It can easily handle multi-dimensional continuous or categorical response variables. MSRL is shown to be consistent in the sense that the conditional probability density function of the response variable given the learned representation converges to the conditional probability density function of the response variable given the predictor. Non-asymptotic error bounds for MSRL are also established under suitable conditions. To establish the error bounds, we derive a generalized Dudley's inequality for an order-two U-process indexed by deep neural networks, which may be of independent interest. We discuss how to determine the intrinsic dimension of the underlying data distribution. Moreover, we evaluate the performance of MSRL via extensive numerical experiments and real data analysis and demonstrate that MSRL outperforms some existing nonlinear sufficient dimension reduction methods.

Estimation of Non-Crossing Quantile Regression Process with Deep ReQU Neural Networks

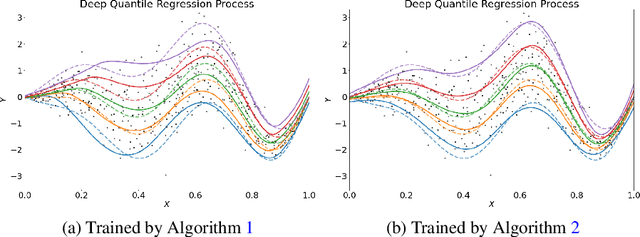
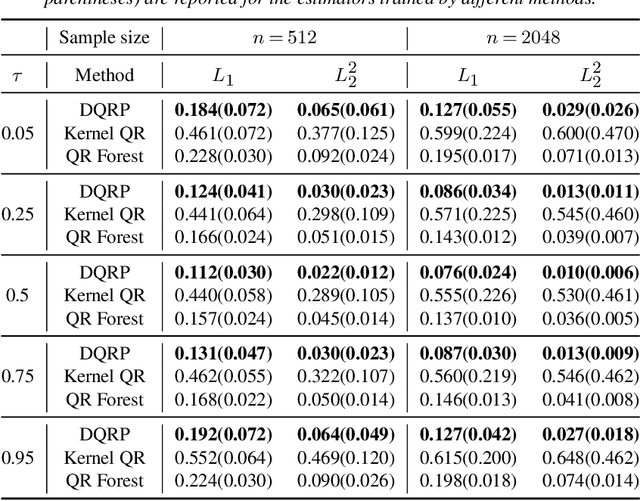
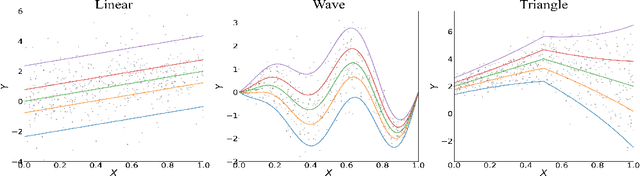
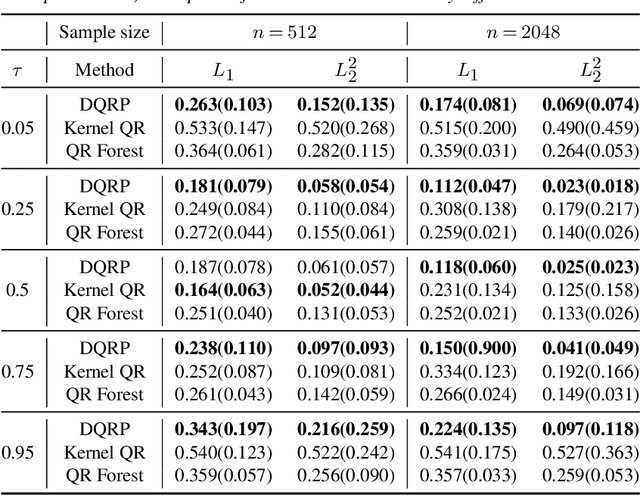
We propose a penalized nonparametric approach to estimating the quantile regression process (QRP) in a nonseparable model using rectifier quadratic unit (ReQU) activated deep neural networks and introduce a novel penalty function to enforce non-crossing of quantile regression curves. We establish the non-asymptotic excess risk bounds for the estimated QRP and derive the mean integrated squared error for the estimated QRP under mild smoothness and regularity conditions. To establish these non-asymptotic risk and estimation error bounds, we also develop a new error bound for approximating $C^s$ smooth functions with $s >0$ and their derivatives using ReQU activated neural networks. This is a new approximation result for ReQU networks and is of independent interest and may be useful in other problems. Our numerical experiments demonstrate that the proposed method is competitive with or outperforms two existing methods, including methods using reproducing kernels and random forests, for nonparametric quantile regression.

Wasserstein Generative Learning of Conditional Distribution

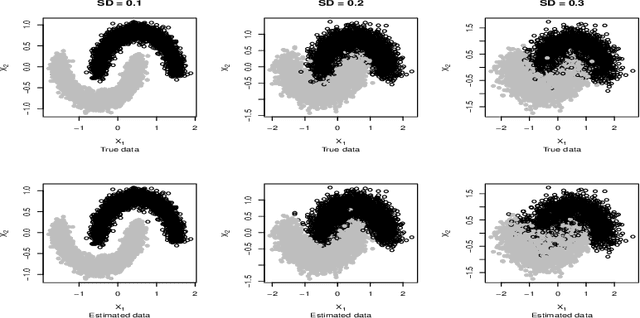
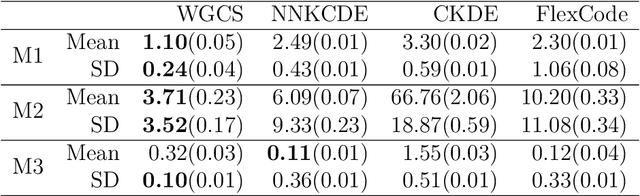
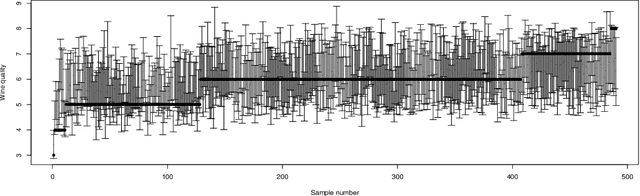
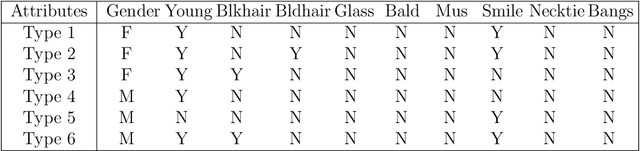
Conditional distribution is a fundamental quantity for describing the relationship between a response and a predictor. We propose a Wasserstein generative approach to learning a conditional distribution. The proposed approach uses a conditional generator to transform a known distribution to the target conditional distribution. The conditional generator is estimated by matching a joint distribution involving the conditional generator and the target joint distribution, using the Wasserstein distance as the discrepancy measure for these joint distributions. We establish non-asymptotic error bound of the conditional sampling distribution generated by the proposed method and show that it is able to mitigate the curse of dimensionality, assuming that the data distribution is supported on a lower-dimensional set. We conduct numerical experiments to validate proposed method and illustrate its applications to conditional sample generation, nonparametric conditional density estimation, prediction uncertainty quantification, bivariate response data, image reconstruction and image generation.

Non-Asymptotic Error Bounds for Bidirectional GANs

We derive nearly sharp bounds for the bidirectional GAN (BiGAN) estimation error under the Dudley distance between the latent joint distribution and the data joint distribution with appropriately specified architecture of the neural networks used in the model. To the best of our knowledge, this is the first theoretical guarantee for the bidirectional GAN learning approach. An appealing feature of our results is that they do not assume the reference and the data distributions to have the same dimensions or these distributions to have bounded support. These assumptions are commonly assumed in the existing convergence analysis of the unidirectional GANs but may not be satisfied in practice. Our results are also applicable to the Wasserstein bidirectional GAN if the target distribution is assumed to have a bounded support. To prove these results, we construct neural network functions that push forward an empirical distribution to another arbitrary empirical distribution on a possibly different-dimensional space. We also develop a novel decomposition of the integral probability metric for the error analysis of bidirectional GANs. These basic theoretical results are of independent interest and can be applied to other related learning problems.

A Learning-based Approach Towards Automated Tuning of SSD Configurations

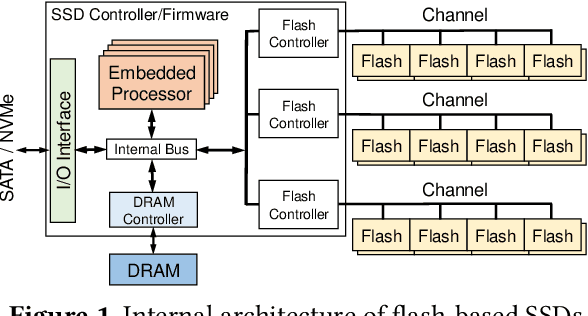
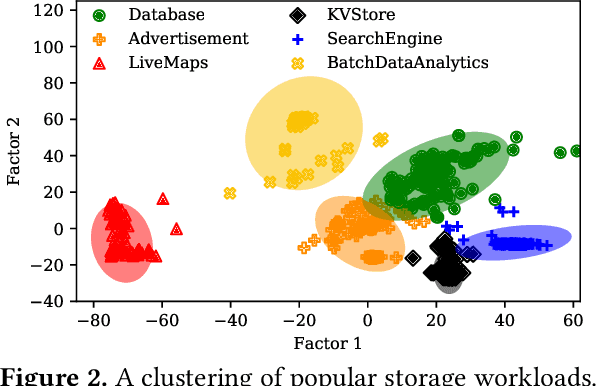
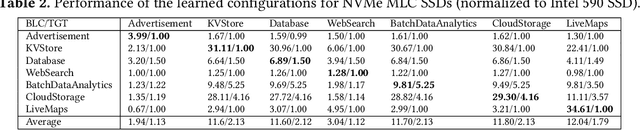
Thanks to the mature manufacturing techniques, solid-state drives (SSDs) are highly customizable for applications today, which brings opportunities to further improve their storage performance and resource utilization. However, the SSD efficiency is usually determined by many hardware parameters, making it hard for developers to manually tune them and determine the optimal SSD configurations. In this paper, we present an automated learning-based framework, named LearnedSSD, that utilizes both supervised and unsupervised machine learning (ML) techniques to drive the tuning of hardware configurations for SSDs. LearnedSSD automatically extracts the unique access patterns of a new workload using its block I/O traces, maps the workload to previously workloads for utilizing the learned experiences, and recommends an optimal SSD configuration based on the validated storage performance. LearnedSSD accelerates the development of new SSD devices by automating the hard-ware parameter configurations and reducing the manual efforts. We develop LearnedSSD with simple yet effective learning algorithms that can run efficiently on multi-core CPUs. Given a target storage workload, our evaluation shows that LearnedSSD can always deliver an optimal SSD configuration for the target workload, and this configuration will not hurt the performance of non-target workloads.

Relative Entropy Gradient Sampler for Unnormalized Distributions

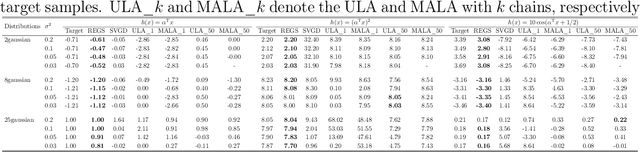
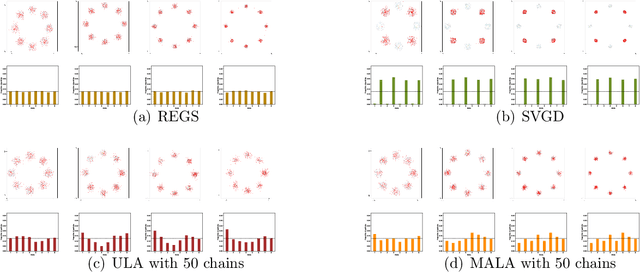
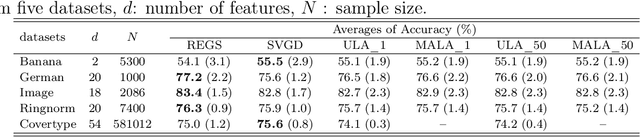
We propose a relative entropy gradient sampler (REGS) for sampling from unnormalized distributions. REGS is a particle method that seeks a sequence of simple nonlinear transforms iteratively pushing the initial samples from a reference distribution into the samples from an unnormalized target distribution. To determine the nonlinear transforms at each iteration, we consider the Wasserstein gradient flow of relative entropy. This gradient flow determines a path of probability distributions that interpolates the reference distribution and the target distribution. It is characterized by an ODE system with velocity fields depending on the density ratios of the density of evolving particles and the unnormalized target density. To sample with REGS, we need to estimate the density ratios and simulate the ODE system with particle evolution. We propose a novel nonparametric approach to estimating the logarithmic density ratio using neural networks. Extensive simulation studies on challenging multimodal 1D and 2D mixture distributions and Bayesian logistic regression on real datasets demonstrate that the REGS outperforms the state-of-the-art sampling methods included in the comparison.

An error analysis of generative adversarial networks for learning distributions

This paper studies how well generative adversarial networks (GANs) learn probability distributions from finite samples. Our main results establish the convergence rates of GANs under a collection of integral probability metrics defined through H\"older classes, including the Wasserstein distance as a special case. We also show that GANs are able to adaptively learn data distributions with low-dimensional structures or have H\"older densities, when the network architectures are chosen properly. In particular, for distributions concentrated around a low-dimensional set, we show that the learning rates of GANs do not depend on the high ambient dimension, but on the lower intrinsic dimension. Our analysis is based on a new oracle inequality decomposing the estimation error into the generator and discriminator approximation error and the statistical error, which may be of independent interest.

Non-asymptotic Excess Risk Bounds for Classification with Deep Convolutional Neural Networks

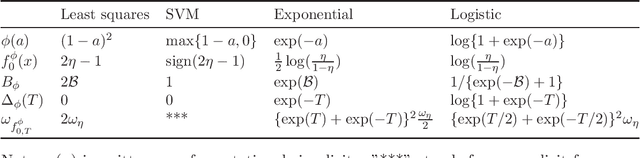
In this paper, we consider the problem of binary classification with a class of general deep convolutional neural networks, which includes fully-connected neural networks and fully convolutional neural networks as special cases. We establish non-asymptotic excess risk bounds for a class of convex surrogate losses and target functions with different modulus of continuity. An important feature of our results is that we clearly define the prefactors of the risk bounds in terms of the input data dimension and other model parameters and show that they depend polynomially on the dimensionality in some important models. We also show that the classification methods with CNNs can circumvent the curse of dimensionality if the input data is supported on an approximate low-dimensional manifold. To establish these results, we derive an upper bound for the covering number for the class of general convolutional neural networks with a bias term in each convolutional layer, and derive new results on the approximation power of CNNs for any uniformly-continuous target functions. These results provide further insights into the complexity and the approximation power of general convolutional neural networks, which are of independent interest and may have other applications. Finally, we apply our general results to analyze the non-asymptotic excess risk bounds for four widely used methods with different loss functions using CNNs, including the least squares, the logistic, the exponential and the SVM hinge losses.

Natural grasp intention recognition based on gaze fixation in human-robot interaction

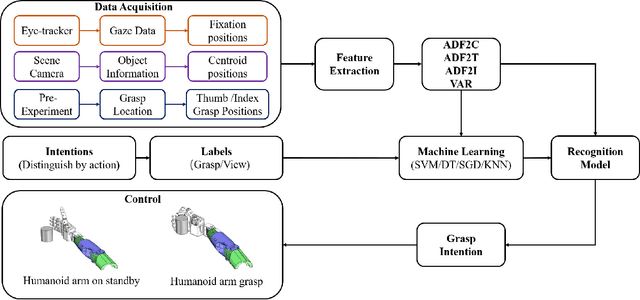
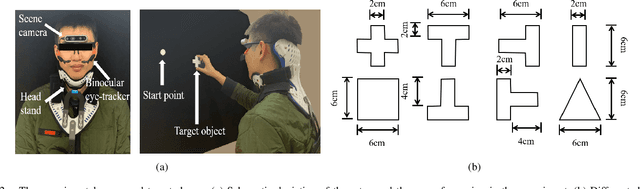
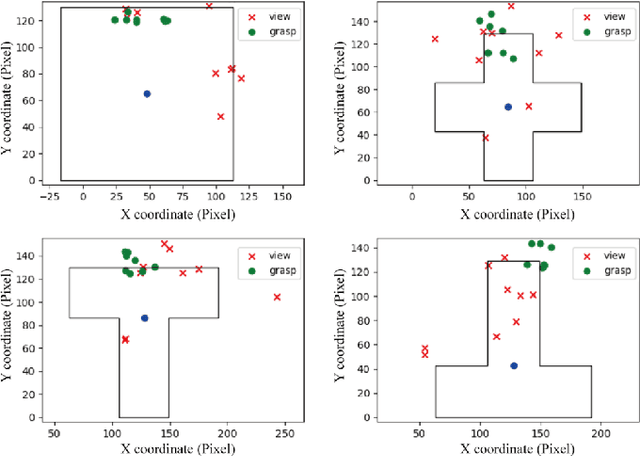
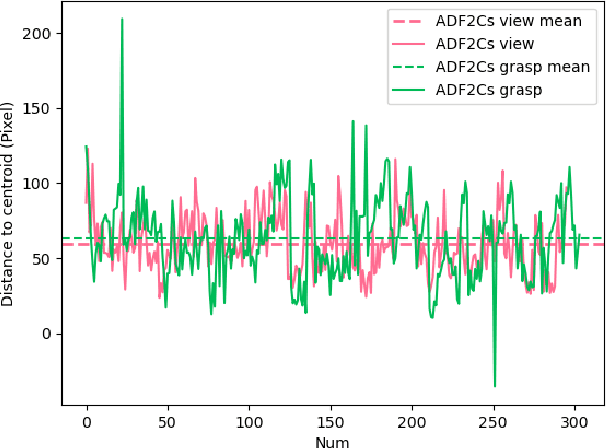
Eye movement is closely related to limb actions, so it can be used to infer movement intentions. More importantly, in some cases, eye movement is the only way for paralyzed and impaired patients with severe movement disorders to communicate and interact with the environment. Despite this, eye-tracking technology still has very limited application scenarios as an intention recognition method. The goal of this paper is to achieve a natural fixation-based grasping intention recognition method, with which a user with hand movement disorders can intuitively express what tasks he/she wants to do by directly looking at the object of interest. Toward this goal, we design experiments to study the relationships of fixations in different tasks. We propose some quantitative features from these relationships and analyze them statistically. Then we design a natural method for grasping intention recognition. The experimental results prove that the accuracy of the proposed method for the grasping intention recognition exceeds 89\% on the training objects. When this method is extendedly applied to objects not included in the training set, the average accuracy exceeds 85\%. The grasping experiment in the actual environment verifies the effectiveness of the proposed method.