LearnLM: Improving Gemini for Learning

Today's generative AI systems are tuned to present information by default rather than engage users in service of learning as a human tutor would. To address the wide range of potential education use cases for these systems, we reframe the challenge of injecting pedagogical behavior as one of \textit{pedagogical instruction following}, where training and evaluation examples include system-level instructions describing the specific pedagogy attributes present or desired in subsequent model turns. This framing avoids committing our models to any particular definition of pedagogy, and instead allows teachers or developers to specify desired model behavior. It also clears a path to improving Gemini models for learning -- by enabling the addition of our pedagogical data to post-training mixtures -- alongside their rapidly expanding set of capabilities. Both represent important changes from our initial tech report. We show how training with pedagogical instruction following produces a LearnLM model (available on Google AI Studio) that is preferred substantially by expert raters across a diverse set of learning scenarios, with average preference strengths of 31\% over GPT-4o, 11\% over Claude 3.5, and 13\% over the Gemini 1.5 Pro model LearnLM was based on.

Learned Ranking Function: From Short-term Behavior Predictions to Long-term User Satisfaction

We present the Learned Ranking Function (LRF), a system that takes short-term user-item behavior predictions as input and outputs a slate of recommendations that directly optimizes for long-term user satisfaction. Most previous work is based on optimizing the hyperparameters of a heuristic function. We propose to model the problem directly as a slate optimization problem with the objective of maximizing long-term user satisfaction. We also develop a novel constraint optimization algorithm that stabilizes objective trade-offs for multi-objective optimization. We evaluate our approach with live experiments and describe its deployment on YouTube.

Analyzing and Improving Greedy 2-Coordinate Updates for Equality-Constrained Optimization via Steepest Descent in the 1-Norm

We consider minimizing a smooth function subject to a summation constraint over its variables. By exploiting a connection between the greedy 2-coordinate update for this problem and equality-constrained steepest descent in the 1-norm, we give a convergence rate for greedy selection under a proximal Polyak-Lojasiewicz assumption that is faster than random selection and independent of the problem dimension $n$. We then consider minimizing with both a summation constraint and bound constraints, as arises in the support vector machine dual problem. Existing greedy rules for this setting either guarantee trivial progress only or require $O(n^2)$ time to compute. We show that bound- and summation-constrained steepest descent in the L1-norm guarantees more progress per iteration than previous rules and can be computed in only $O(n \log n)$ time.

Agent-Time Attention for Sparse Rewards Multi-Agent Reinforcement Learning

Sparse and delayed rewards pose a challenge to single agent reinforcement learning. This challenge is amplified in multi-agent reinforcement learning (MARL) where credit assignment of these rewards needs to happen not only across time, but also across agents. We propose Agent-Time Attention (ATA), a neural network model with auxiliary losses for redistributing sparse and delayed rewards in collaborative MARL. We provide a simple example that demonstrates how providing agents with their own local redistributed rewards and shared global redistributed rewards motivate different policies. We extend several MiniGrid environments, specifically MultiRoom and DoorKey, to the multi-agent sparse delayed rewards setting. We demonstrate that ATA outperforms various baselines on many instances of these environments. Source code of the experiments is available at https://github.com/jshe/agent-time-attention.

TF-GNN: Graph Neural Networks in TensorFlow

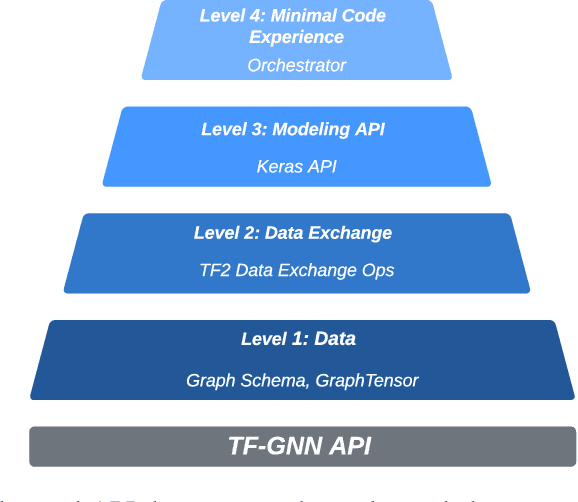
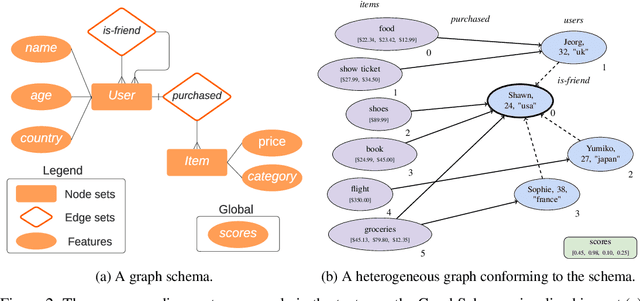
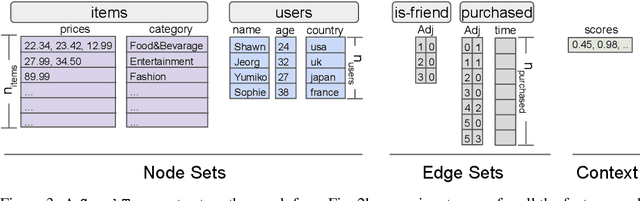
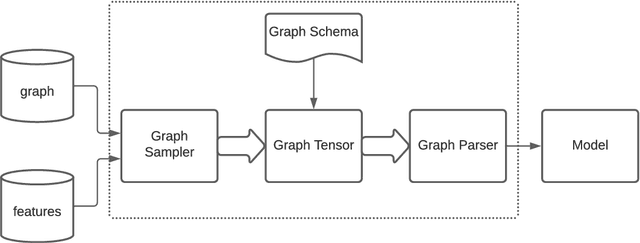
TensorFlow GNN (TF-GNN) is a scalable library for Graph Neural Networks in TensorFlow. It is designed from the bottom up to support the kinds of rich heterogeneous graph data that occurs in today's information ecosystems. Many production models at Google use TF-GNN and it has been recently released as an open source project. In this paper, we describe the TF-GNN data model, its Keras modeling API, and relevant capabilities such as graph sampling, distributed training, and accelerator support.

ETA Prediction with Graph Neural Networks in Google Maps

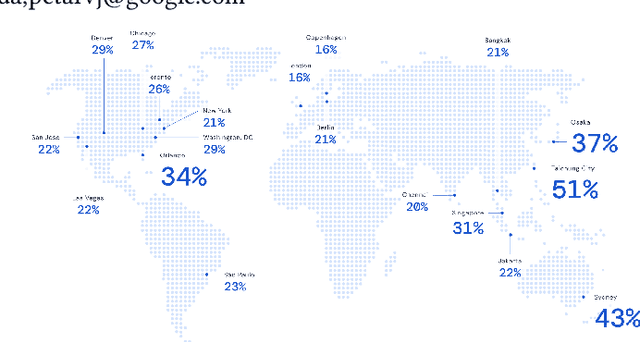
Travel-time prediction constitutes a task of high importance in transportation networks, with web mapping services like Google Maps regularly serving vast quantities of travel time queries from users and enterprises alike. Further, such a task requires accounting for complex spatiotemporal interactions (modelling both the topological properties of the road network and anticipating events -- such as rush hours -- that may occur in the future). Hence, it is an ideal target for graph representation learning at scale. Here we present a graph neural network estimator for estimated time of arrival (ETA) which we have deployed in production at Google Maps. While our main architecture consists of standard GNN building blocks, we further detail the usage of training schedule methods such as MetaGradients in order to make our model robust and production-ready. We also provide prescriptive studies: ablating on various architectural decisions and training regimes, and qualitative analyses on real-world situations where our model provides a competitive edge. Our GNN proved powerful when deployed, significantly reducing negative ETA outcomes in several regions compared to the previous production baseline (40+% in cities like Sydney).

Adversarial Computation of Optimal Transport Maps

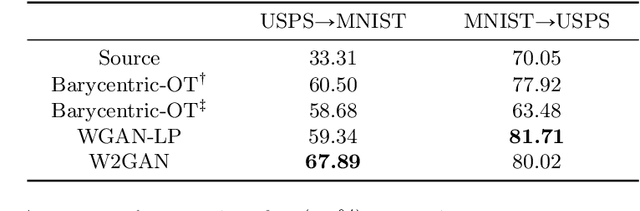
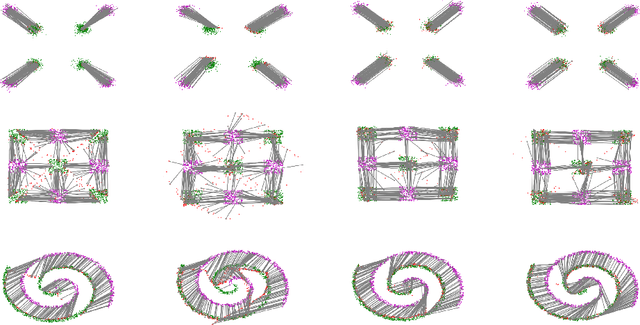
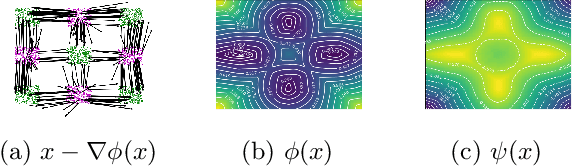
Computing optimal transport maps between high-dimensional and continuous distributions is a challenging problem in optimal transport (OT). Generative adversarial networks (GANs) are powerful generative models which have been successfully applied to learn maps across high-dimensional domains. However, little is known about the nature of the map learned with a GAN objective. To address this problem, we propose a generative adversarial model in which the discriminator's objective is the $2$-Wasserstein metric. We show that during training, our generator follows the $W_2$-geodesic between the initial and the target distributions. As a consequence, it reproduces an optimal map at the end of training. We validate our approach empirically in both low-dimensional and high-dimensional continuous settings, and show that it outperforms prior methods on image data.