Faster Convergence of Stochastic Accelerated Gradient Descent under Interpolation

We prove new convergence rates for a generalized version of stochastic Nesterov acceleration under interpolation conditions. Unlike previous analyses, our approach accelerates any stochastic gradient method which makes sufficient progress in expectation. The proof, which proceeds using the estimating sequences framework, applies to both convex and strongly convex functions and is easily specialized to accelerated SGD under the strong growth condition. In this special case, our analysis reduces the dependence on the strong growth constant from $\rho$ to $\sqrt{\rho}$ as compared to prior work. This improvement is comparable to a square-root of the condition number in the worst case and address criticism that guarantees for stochastic acceleration could be worse than those for SGD.

Directional Smoothness and Gradient Methods: Convergence and Adaptivity

We develop new sub-optimality bounds for gradient descent (GD) that depend on the conditioning of the objective along the path of optimization, rather than on global, worst-case constants. Key to our proofs is directional smoothness, a measure of gradient variation that we use to develop upper-bounds on the objective. Minimizing these upper-bounds requires solving implicit equations to obtain a sequence of strongly adapted step-sizes; we show that these equations are straightforward to solve for convex quadratics and lead to new guarantees for two classical step-sizes. For general functions, we prove that the Polyak step-size and normalized GD obtain fast, path-dependent rates despite using no knowledge of the directional smoothness. Experiments on logistic regression show our convergence guarantees are tighter than the classical theory based on L-smoothness.

Level Set Teleportation: An Optimization Perspective

We study level set teleportation, an optimization sub-routine which seeks to accelerate gradient methods by maximizing the gradient norm on a level-set of the objective function. Since the descent lemma implies that gradient descent (GD) decreases the objective proportional to the squared norm of the gradient, level-set teleportation maximizes this one-step progress guarantee. For convex functions satisfying Hessian stability, we prove that GD with level-set teleportation obtains a combined sub-linear/linear convergence rate which is strictly faster than standard GD when the optimality gap is small. This is in sharp contrast to the standard (strongly) convex setting, where we show level-set teleportation neither improves nor worsens convergence rates. To evaluate teleportation in practice, we develop a projected-gradient-type method requiring only Hessian-vector products. We use this method to show that gradient methods with access to a teleportation oracle uniformly out-perform their standard versions on a variety of learning problems.

A Library of Mirrors: Deep Neural Nets in Low Dimensions are Convex Lasso Models with Reflection Features

We prove that training neural networks on 1-D data is equivalent to solving a convex Lasso problem with a fixed, explicitly defined dictionary matrix of features. The specific dictionary depends on the activation and depth. We consider 2-layer networks with piecewise linear activations, deep narrow ReLU networks with up to 4 layers, and rectangular and tree networks with sign activation and arbitrary depth. Interestingly in ReLU networks, a fourth layer creates features that represent reflections of training data about themselves. The Lasso representation sheds insight to globally optimal networks and the solution landscape.

Analyzing and Improving Greedy 2-Coordinate Updates for Equality-Constrained Optimization via Steepest Descent in the 1-Norm

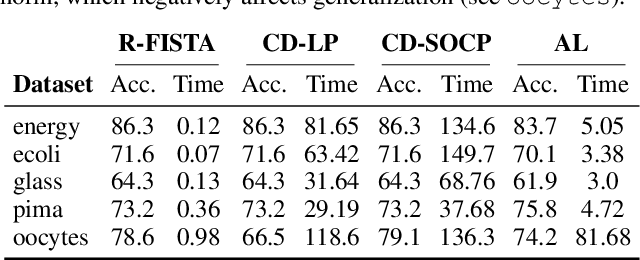
We consider minimizing a smooth function subject to a summation constraint over its variables. By exploiting a connection between the greedy 2-coordinate update for this problem and equality-constrained steepest descent in the 1-norm, we give a convergence rate for greedy selection under a proximal Polyak-Lojasiewicz assumption that is faster than random selection and independent of the problem dimension $n$. We then consider minimizing with both a summation constraint and bound constraints, as arises in the support vector machine dual problem. Existing greedy rules for this setting either guarantee trivial progress only or require $O(n^2)$ time to compute. We show that bound- and summation-constrained steepest descent in the L1-norm guarantees more progress per iteration than previous rules and can be computed in only $O(n \log n)$ time.

Optimal Sets and Solution Paths of ReLU Networks

We develop an analytical framework to characterize the set of optimal ReLU neural networks by reformulating the non-convex training problem as a convex program. We show that the global optima of the convex parameterization are given by a polyhedral set and then extend this characterization to the optimal set of the non-convex training objective. Since all stationary points of the ReLU training problem can be represented as optima of sub-sampled convex programs, our work provides a general expression for all critical points of the non-convex objective. We then leverage our results to provide an optimal pruning algorithm for computing minimal networks, establish conditions for the regularization path of ReLU networks to be continuous, and develop sensitivity results for minimal ReLU networks.

Fast Convex Optimization for Two-Layer ReLU Networks: Equivalent Model Classes and Cone Decompositions

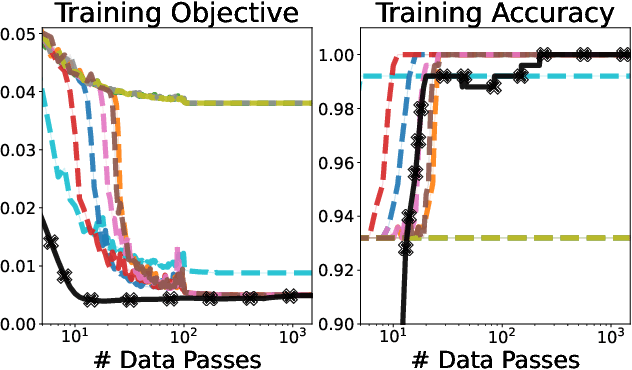
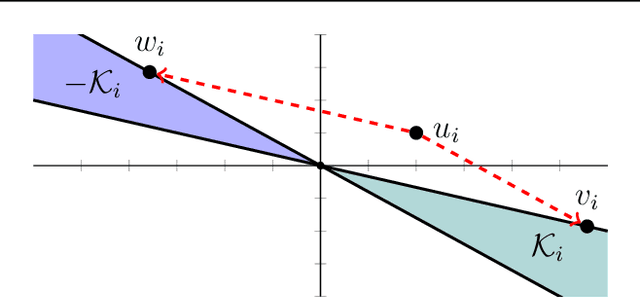
We develop fast algorithms and robust software for convex optimization of two-layer neural networks with ReLU activation functions. Our work leverages a convex reformulation of the standard weight-decay penalized training problem as a set of group-$\ell_1$-regularized data-local models, where locality is enforced by polyhedral cone constraints. In the special case of zero-regularization, we show that this problem is exactly equivalent to unconstrained optimization of a convex "gated ReLU" network. For problems with non-zero regularization, we show that convex gated ReLU models obtain data-dependent approximation bounds for the ReLU training problem. To optimize the convex reformulations, we develop an accelerated proximal gradient method and a practical augmented Lagrangian solver. We show that these approaches are faster than standard training heuristics for the non-convex problem, such as SGD, and outperform commercial interior-point solvers. Experimentally, we verify our theoretical results, explore the group-$\ell_1$ regularization path, and scale convex optimization for neural networks to image classification on MNIST and CIFAR-10.

To Each Optimizer a Norm, To Each Norm its Generalization

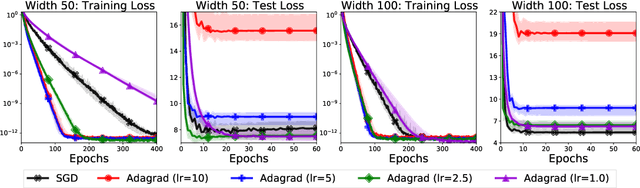
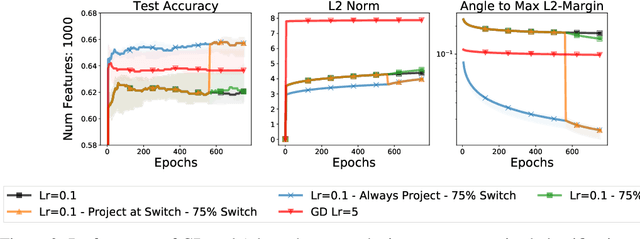
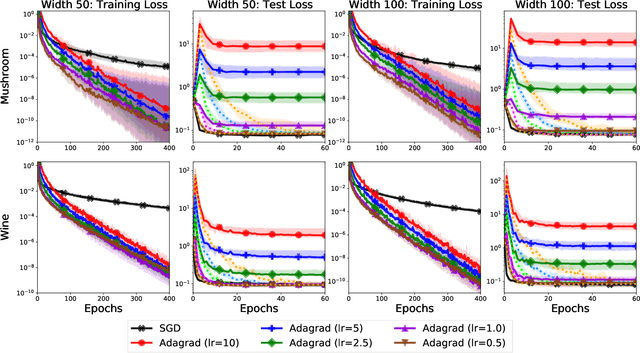
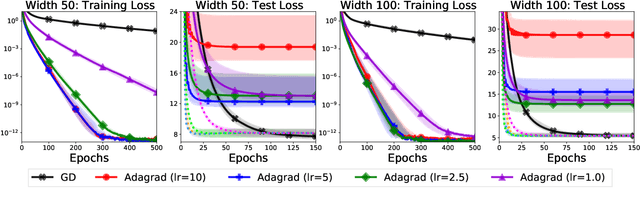
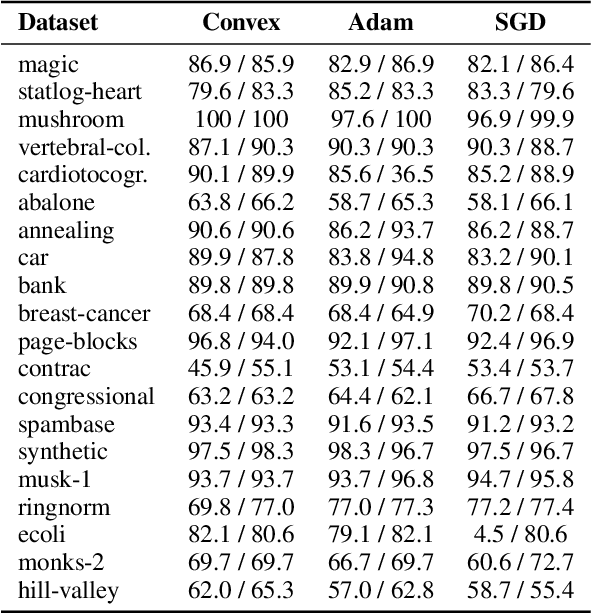
We study the implicit regularization of optimization methods for linear models interpolating the training data in the under-parametrized and over-parametrized regimes. Since it is difficult to determine whether an optimizer converges to solutions that minimize a known norm, we flip the problem and investigate what is the corresponding norm minimized by an interpolating solution. Using this reasoning, we prove that for over-parameterized linear regression, projections onto linear spans can be used to move between different interpolating solutions. For under-parameterized linear classification, we prove that for any linear classifier separating the data, there exists a family of quadratic norms ||.||_P such that the classifier's direction is the same as that of the maximum P-margin solution. For linear classification, we argue that analyzing convergence to the standard maximum l2-margin is arbitrary and show that minimizing the norm induced by the data results in better generalization. Furthermore, for over-parameterized linear classification, projections onto the data-span enable us to use techniques from the under-parameterized setting. On the empirical side, we propose techniques to bias optimizers towards better generalizing solutions, improving their test performance. We validate our theoretical results via synthetic experiments, and use the neural tangent kernel to handle non-linear models.

Painless Stochastic Gradient: Interpolation, Line-Search, and Convergence Rates

Recent works have shown that stochastic gradient descent (SGD) achieves the fast convergence rates of full-batch gradient descent for over-parameterized models satisfying certain interpolation conditions. However, the step-size used in these works depends on unknown quantities, and SGD's practical performance heavily relies on the choice of the step-size. We propose to use line-search methods to automatically set the step-size when training models that can interpolate the data. We prove that SGD with the classic Armijo line-search attains the fast convergence rates of full-batch gradient descent in convex and strongly-convex settings. We also show that under additional assumptions, SGD with a modified line-search can attain a fast rate of convergence for non-convex functions. Furthermore, we show that a stochastic extra-gradient method with a Lipschitz line-search attains a fast convergence rate for an important class of non-convex functions and saddle-point problems satisfying interpolation. We then give heuristics to use larger step-sizes and acceleration with our line-search techniques. We compare the proposed algorithms against numerous optimization methods for standard classification tasks using both kernel methods and deep networks. The proposed methods are robust and result in competitive performance across all models and datasets. Moreover, for the deep network models, SGD with our line-search results in both faster convergence and better generalization.

SLANG: Fast Structured Covariance Approximations for Bayesian Deep Learning with Natural Gradient

Uncertainty estimation in large deep-learning models is a computationally challenging task, where it is difficult to form even a Gaussian approximation to the posterior distribution. In such situations, existing methods usually resort to a diagonal approximation of the covariance matrix despite, the fact that these matrices are known to give poor uncertainty estimates. To address this issue, we propose a new stochastic, low-rank, approximate natural-gradient (SLANG) method for variational inference in large, deep models. Our method estimates a "diagonal plus low-rank" structure based solely on back-propagated gradients of the network log-likelihood. This requires strictly less gradient computations than methods that compute the gradient of the whole variational objective. Empirical evaluations on standard benchmarks confirm that SLANG enables faster and more accurate estimation of uncertainty than mean-field methods, and performs comparably to state-of-the-art methods.