Concept Algebra for Text-Controlled Vision Models

This paper concerns the control of text-guided generative models, where a user provides a natural language prompt and the model generates samples based on this input. Prompting is intuitive, general, and flexible. However, there are significant limitations: prompting can fail in surprising ways, and it is often unclear how to find a prompt that will elicit some desired target behavior. A core difficulty for developing methods to overcome these issues is that failures are know-it-when-you-see-it -- it's hard to fix bugs if you can't state precisely what the model should have done! In this paper, we introduce a formalization of "what the user intended" in terms of latent concepts implicit to the data generating process that the model was trained on. This formalization allows us to identify some fundamental limitations of prompting. We then use the formalism to develop concept algebra to overcome these limitations. Concept algebra is a way of directly manipulating the concepts expressed in the output through algebraic operations on a suitably defined representation of input prompts. We give examples using concept algebra to overcome limitations of prompting, including concept transfer through arithmetic, and concept nullification through projection. Code available at https://github.com/zihao12/concept-algebra.

Statistical Inference with Stochastic Gradient Algorithms

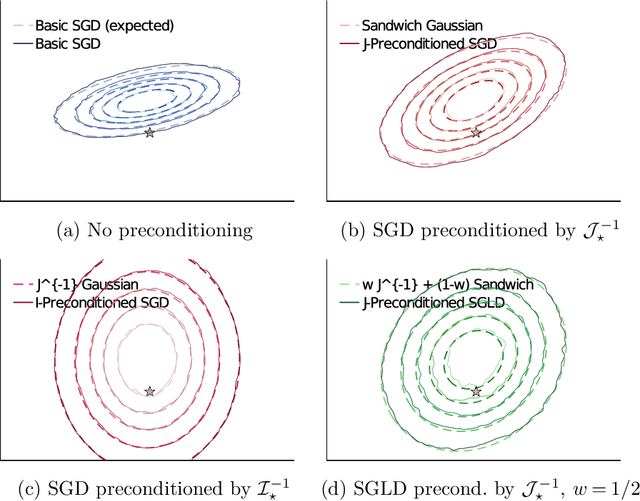
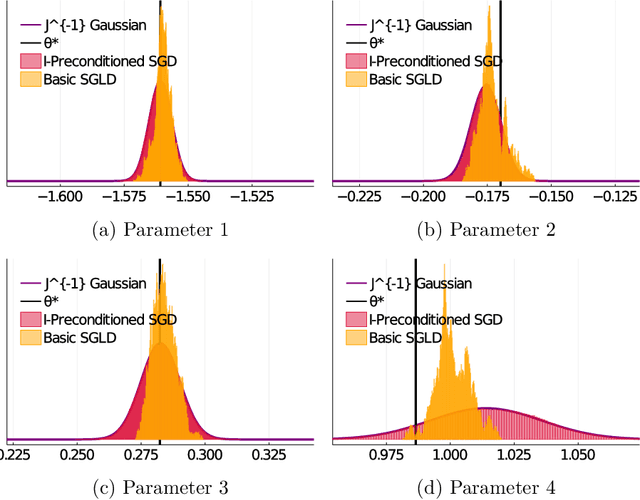
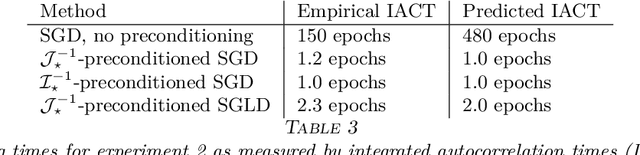
Stochastic gradient algorithms are widely used for both optimization and sampling in large-scale learning and inference problems. However, in practice, tuning these algorithms is typically done using heuristics and trial-and-error rather than rigorous, generalizable theory. To address this gap between theory and practice, we novel insights into the effect of tuning parameters by characterizing the large-sample behavior of iterates of a very general class of preconditioned stochastic gradient algorithms with fixed step size. In the optimization setting, our results show that iterate averaging with a large fixed step size can result in statistically efficient approximation of the (local) M-estimator. In the sampling context, our results show that with appropriate choices of tuning parameters, the limiting stationary covariance can match either the Bernstein--von Mises limit of the posterior, adjustments to the posterior for model misspecification, or the asymptotic distribution of the MLE; and that with a naive tuning the limit corresponds to none of these. Moreover, we argue that an essentially independent sample from the stationary distribution can be obtained after a fixed number of passes over the dataset. We validate our asymptotic results in realistic finite-sample regimes via several experiments using simulated and real data. Overall, we demonstrate that properly tuned stochastic gradient algorithms with constant step size offer a computationally efficient and statistically robust approach to obtaining point estimates or posterior-like samples.

Minimax Optimal Quantile and Semi-Adversarial Regret via Root-Logarithmic Regularizers

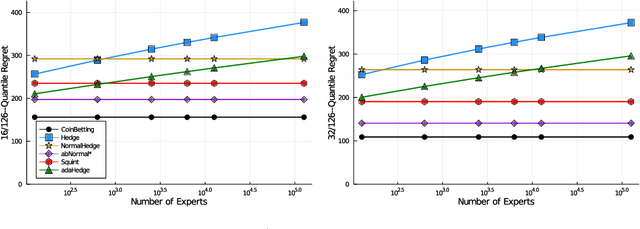
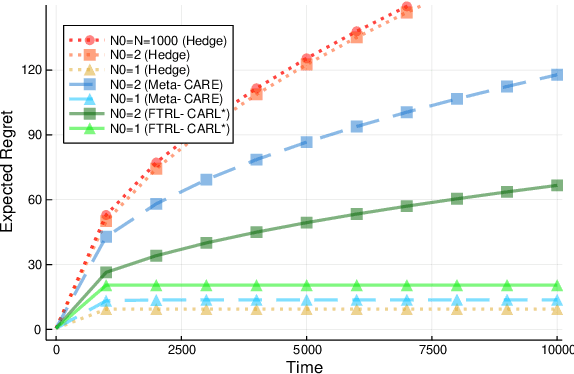
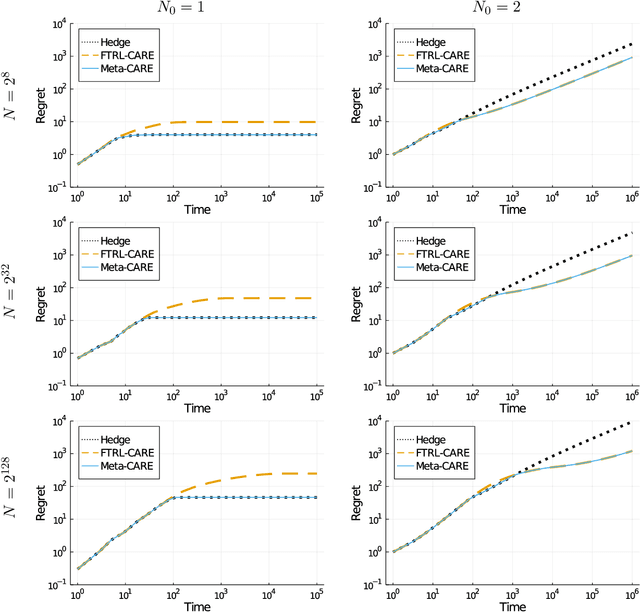
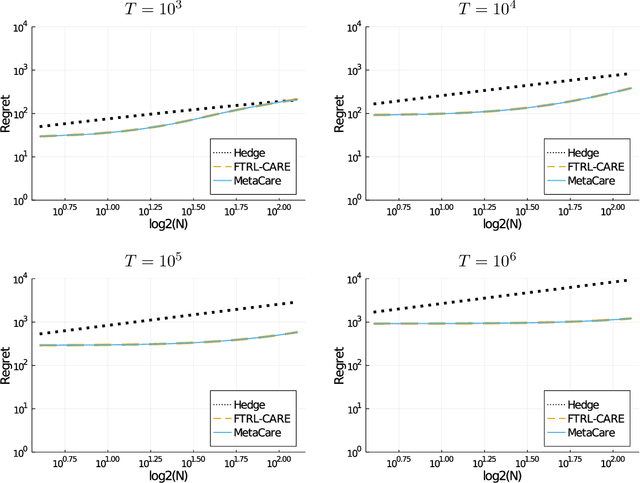
Quantile (and, more generally, KL) regret bounds, such as those achieved by NormalHedge (Chaudhuri, Freund, and Hsu 2009) and its variants, relax the goal of competing against the best individual expert to only competing against a majority of experts on adversarial data. More recently, the semi-adversarial paradigm (Bilodeau, Negrea, and Roy 2020) provides an alternative relaxation of adversarial online learning by considering data that may be neither fully adversarial nor stochastic (i.i.d.). We achieve the minimax optimal regret in both paradigms using FTRL with separate, novel, root-logarithmic regularizers, both of which can be interpreted as yielding variants of NormalHedge. We extend existing KL regret upper bounds, which hold uniformly over target distributions, to possibly uncountable expert classes with arbitrary priors; provide the first full-information lower bounds for quantile regret on finite expert classes (which are tight); and provide an adaptively minimax optimal algorithm for the semi-adversarial paradigm that adapts to the true, unknown constraint faster, leading to uniformly improved regret bounds over existing methods.

Relaxing the I.I.D. Assumption: Adaptive Minimax Optimal Sequential Prediction with Expert Advice

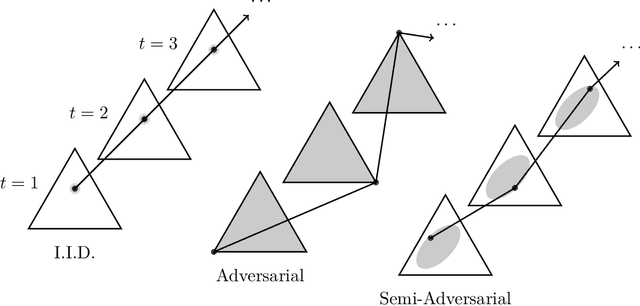
We consider sequential prediction with expert advice when the data are generated stochastically, but the distributions generating the data may vary arbitrarily among some constraint set. We quantify relaxations of the classical I.I.D. assumption in terms of possible constraint sets, with I.I.D. at one extreme, and an adversarial mechanism at the other. The Hedge algorithm, long known to be minimax optimal in the adversarial regime, has recently been shown to also be minimax optimal in the I.I.D. setting. We show that Hedge is suboptimal between these extremes, and present a new algorithm that is adaptively minimax optimal with respect to our relaxations of the I.I.D. assumption, without knowledge of which setting prevails.

Sharpened Generalization Bounds based on Conditional Mutual Information and an Application to Noisy, Iterative Algorithms

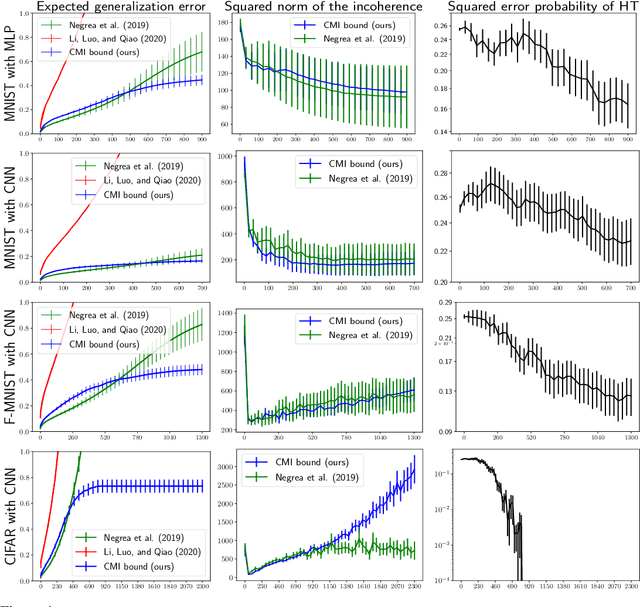
The information-theoretic framework of Russo and J. Zou (2016) and Xu and Raginsky (2017) provides bounds on the generalization error of a learning algorithm in terms of the mutual information between the algorithm's output and the training sample. In this work, we study the proposal, by Steinke and Zakynthinou (2020), to reason about the generalization error of a learning algorithm by introducing a super sample that contains the training sample as a random subset and computing mutual information conditional on the super sample. We first show that these new bounds based on the conditional mutual information are tighter than those based on the unconditional mutual information. We then introduce yet tighter bounds, building on the "individual sample" idea of Bu, S. Zou, and Veeravalli (2019) and the "data dependent" ideas of Negrea et al. (2019), using disintegrated mutual information. Finally, we apply these bounds to the study of Langevin dynamics algorithm, showing that conditioning on the super sample allows us to exploit information in the optimization trajectory to obtain tighter bounds based on hypothesis tests.

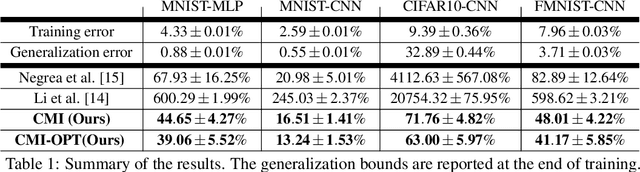
In Defense of Uniform Convergence: Generalization via derandomization with an application to interpolating predictors

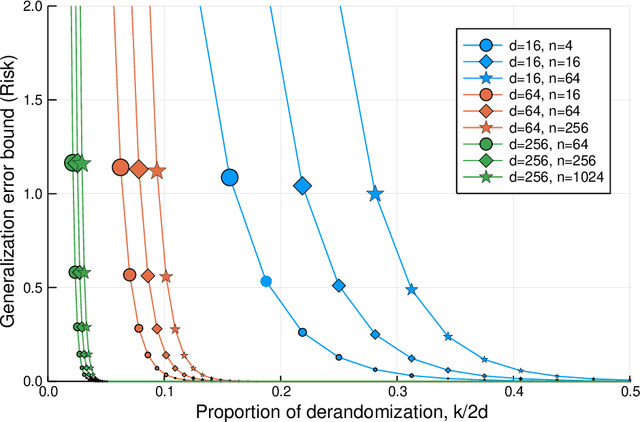
We propose to study the generalization error of a learned predictor $\hat h$ in terms of that of a surrogate (potentially randomized) classifier that is coupled to $\hat h$ and designed to trade empirical risk for control of generalization error. In the case where $\hat h$ interpolates the data, it is interesting to consider theoretical surrogate classifiers that are partially derandomized or rerandomized, e.g., fit to the training data but with modified label noise. We show that replacing $\hat h$ by its conditional distribution with respect to an arbitrary $\sigma$-field is a viable method to derandomize. We give an example, inspired by the work of Nagarajan and Kolter (2019), where the learned classifier $\hat h$ interpolates the training data with high probability, has small risk, and, yet, does not belong to a nonrandom class with a tight uniform bound on two-sided generalization error. At the same time, we bound the risk of $\hat h$ in terms of a surrogate that is constructed by conditioning and shown to belong to a nonrandom class with uniformly small generalization error.

Information-Theoretic Generalization Bounds for SGLD via Data-Dependent Estimates

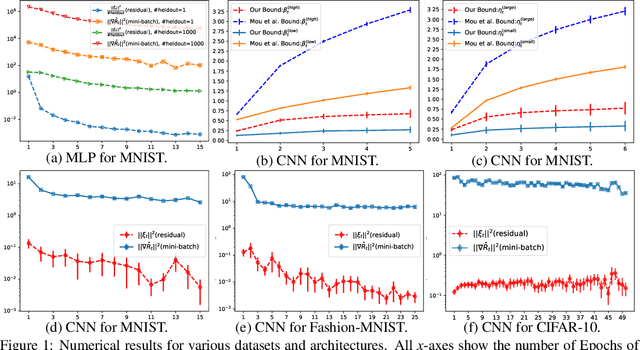
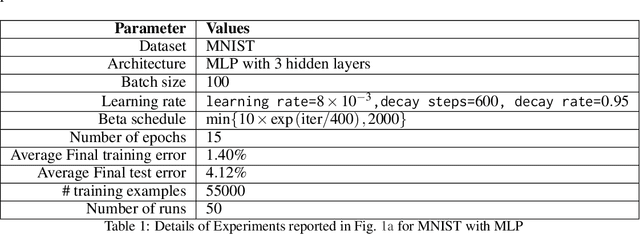
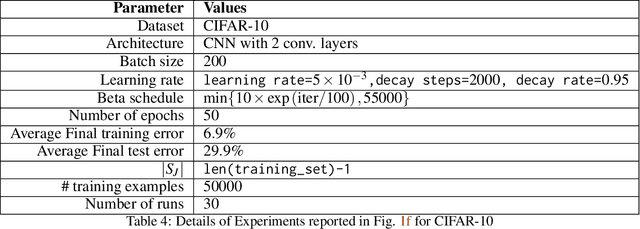
In this work, we improve upon the stepwise analysis of noisy iterative learning algorithms initiated by Pensia, Jog, and Loh (2018) and recently extended by Bu, Zou, and Veeravalli (2019). Our main contributions are significantly improved mutual information bounds for Stochastic Gradient Langevin Dynamics via data-dependent estimates. Our approach is based on the variational characterization of mutual information and the use of data-dependent priors that forecast the mini-batch gradient based on a subset of the training samples. Our approach is broadly applicable within the information-theoretic framework of Russo and Zou (2015) and Xu and Raginsky (2017). Our bound can be tied to a measure of flatness of the empirical risk surface. As compared with other bounds that depend on the squared norms of gradients, empirical investigations show that the terms in our bounds are orders of magnitude smaller.