Tuning-free coreset Markov chain Monte Carlo

A Bayesian coreset is a small, weighted subset of a data set that replaces the full data during inference to reduce computational cost. The state-of-the-art coreset construction algorithm, Coreset Markov chain Monte Carlo (Coreset MCMC), uses draws from an adaptive Markov chain targeting the coreset posterior to train the coreset weights via stochastic gradient optimization. However, the quality of the constructed coreset, and thus the quality of its posterior approximation, is sensitive to the stochastic optimization learning rate. In this work, we propose a learning-rate-free stochastic gradient optimization procedure, Hot-start Distance over Gradient (Hot DoG), for training coreset weights in Coreset MCMC without user tuning effort. Empirical results demonstrate that Hot DoG provides higher quality posterior approximations than other learning-rate-free stochastic gradient methods, and performs competitively to optimally-tuned ADAM.

Reproducible Parameter Inference Using Bagged Posteriors

Under model misspecification, it is known that Bayesian posteriors often do not properly quantify uncertainty about true or pseudo-true parameters. Even more fundamentally, misspecification leads to a lack of reproducibility in the sense that the same model will yield contradictory posteriors on independent data sets from the true distribution. To define a criterion for reproducible uncertainty quantification under misspecification, we consider the probability that two confidence sets constructed from independent data sets have nonempty overlap, and we establish a lower bound on this overlap probability that holds for any valid confidence sets. We prove that credible sets from the standard posterior can strongly violate this bound, particularly in high-dimensional settings (i.e., with dimension increasing with sample size), indicating that it is not internally coherent under misspecification. To improve reproducibility in an easy-to-use and widely applicable way, we propose to apply bagging to the Bayesian posterior ("BayesBag"'); that is, to use the average of posterior distributions conditioned on bootstrapped datasets. We motivate BayesBag from first principles based on Jeffrey conditionalization and show that the bagged posterior typically satisfies the overlap lower bound. Further, we prove a Bernstein--Von Mises theorem for the bagged posterior, establishing its asymptotic normal distribution. We demonstrate the benefits of BayesBag via simulation experiments and an application to crime rate prediction.

A Targeted Accuracy Diagnostic for Variational Approximations

Variational Inference (VI) is an attractive alternative to Markov Chain Monte Carlo (MCMC) due to its computational efficiency in the case of large datasets and/or complex models with high-dimensional parameters. However, evaluating the accuracy of variational approximations remains a challenge. Existing methods characterize the quality of the whole variational distribution, which is almost always poor in realistic applications, even if specific posterior functionals such as the component-wise means or variances are accurate. Hence, these diagnostics are of practical value only in limited circumstances. To address this issue, we propose the TArgeted Diagnostic for Distribution Approximation Accuracy (TADDAA), which uses many short parallel MCMC chains to obtain lower bounds on the error of each posterior functional of interest. We also develop a reliability check for TADDAA to determine when the lower bounds should not be trusted. Numerical experiments validate the practical utility and computational efficiency of our approach on a range of synthetic distributions and real-data examples, including sparse logistic regression and Bayesian neural network models.

Statistical Inference with Stochastic Gradient Algorithms

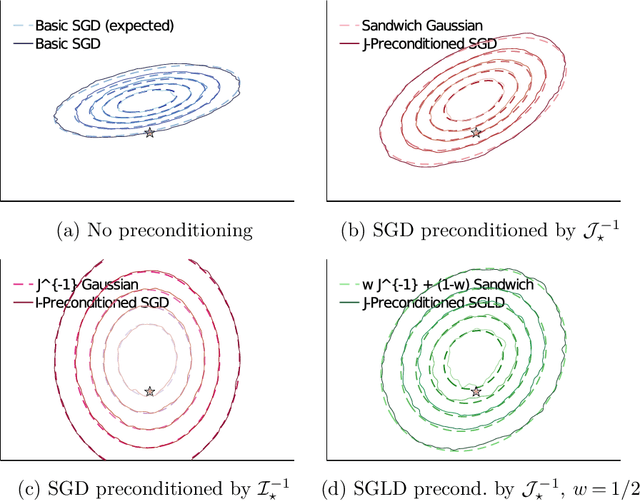
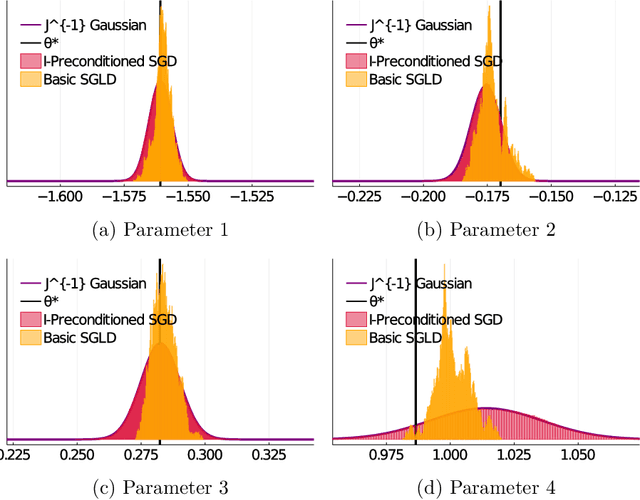
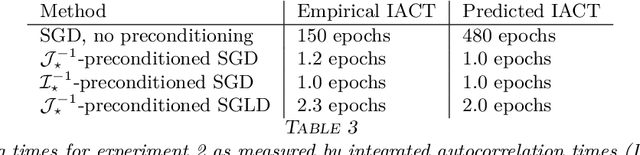
Stochastic gradient algorithms are widely used for both optimization and sampling in large-scale learning and inference problems. However, in practice, tuning these algorithms is typically done using heuristics and trial-and-error rather than rigorous, generalizable theory. To address this gap between theory and practice, we novel insights into the effect of tuning parameters by characterizing the large-sample behavior of iterates of a very general class of preconditioned stochastic gradient algorithms with fixed step size. In the optimization setting, our results show that iterate averaging with a large fixed step size can result in statistically efficient approximation of the (local) M-estimator. In the sampling context, our results show that with appropriate choices of tuning parameters, the limiting stationary covariance can match either the Bernstein--von Mises limit of the posterior, adjustments to the posterior for model misspecification, or the asymptotic distribution of the MLE; and that with a naive tuning the limit corresponds to none of these. Moreover, we argue that an essentially independent sample from the stationary distribution can be obtained after a fixed number of passes over the dataset. We validate our asymptotic results in realistic finite-sample regimes via several experiments using simulated and real data. Overall, we demonstrate that properly tuned stochastic gradient algorithms with constant step size offer a computationally efficient and statistically robust approach to obtaining point estimates or posterior-like samples.

Robust, Automated, and Accurate Black-box Variational Inference

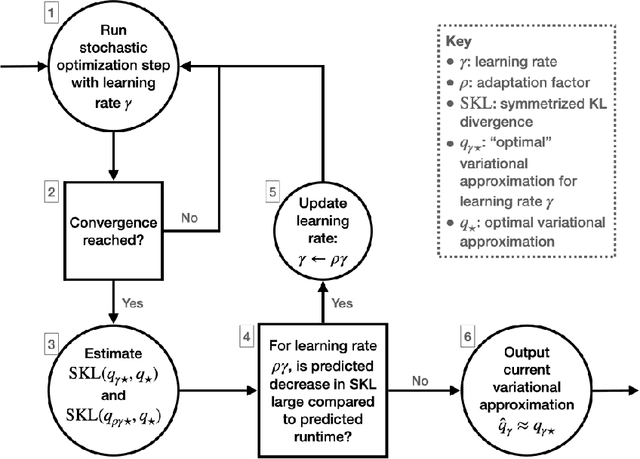
Black-box variational inference (BBVI) now sees widespread use in machine learning and statistics as a fast yet flexible alternative to Markov chain Monte Carlo methods for approximate Bayesian inference. However, stochastic optimization methods for BBVI remain unreliable and require substantial expertise and hand-tuning to apply effectively. In this paper, we propose Robust, Automated, and Accurate BBVI (RAABBVI), a framework for reliable BBVI optimization. RAABBVI is based on rigorously justified automation techniques, includes just a small number of intuitive tuning parameters, and detects inaccurate estimates of the optimal variational approximation. RAABBVI adaptively decreases the learning rate by detecting convergence of the fixed--learning-rate iterates, then estimates the symmetrized Kullback--Leiber (KL) divergence between the current variational approximation and the optimal one. It also employs a novel optimization termination criterion that enables the user to balance desired accuracy against computational cost by comparing (i) the predicted relative decrease in the symmetrized KL divergence if a smaller learning were used and (ii) the predicted computation required to converge with the smaller learning rate. We validate the robustness and accuracy of RAABBVI through carefully designed simulation studies and on a diverse set of real-world model and data examples.

Robust, Accurate Stochastic Optimization for Variational Inference

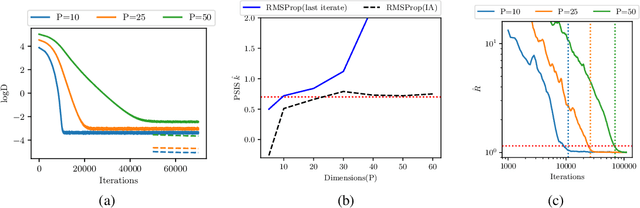
We consider the problem of fitting variational posterior approximations using stochastic optimization methods. The performance of these approximations depends on (1) how well the variational family matches the true posterior distribution,(2) the choice of divergence, and (3) the optimization of the variational objective. We show that even in the best-case scenario when the exact posterior belongs to the assumed variational family, common stochastic optimization methods lead to poor variational approximations if the problem dimension is moderately large. We also demonstrate that these methods are not robust across diverse model types. Motivated by these findings, we develop a more robust and accurate stochastic optimization framework by viewing the underlying optimization algorithm as producing a Markov chain. Our approach is theoretically motivated and includes a diagnostic for convergence and a novel stopping rule, both of which are robust to noisy evaluations of the objective function. We show empirically that the proposed framework works well on a diverse set of models: it can automatically detect stochastic optimization failure or inaccurate variational approximation

Practical Posterior Error Bounds from Variational Objectives

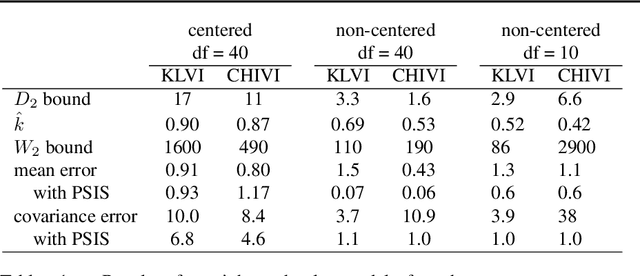
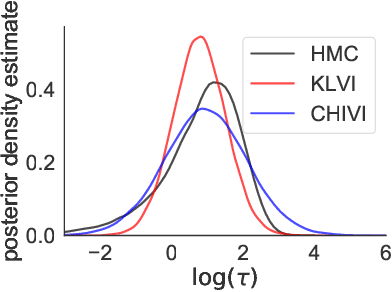
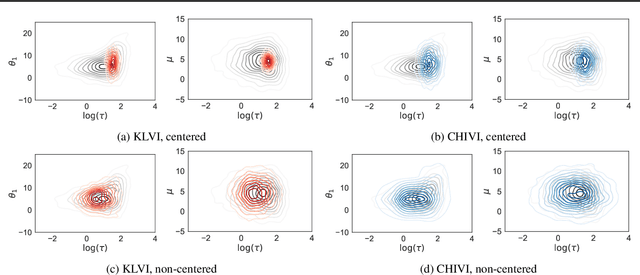
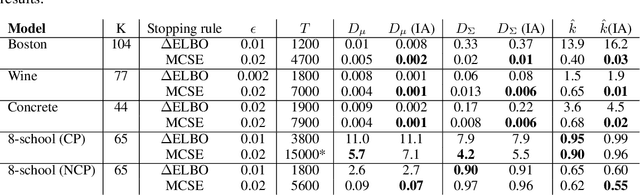
Variational inference has become an increasingly attractive fast alternative to Markov chain Monte Carlo methods for approximate Bayesian inference. However, a major obstacle to the widespread use of variational methods is the lack of post-hoc accuracy measures that are both theoretically justified and computationally efficient. In this paper, we provide rigorous bounds on the error of posterior mean and uncertainty estimates that arise from full-distribution approximations, as in variational inference. Our bounds are widely applicable as they require only that the approximating and exact posteriors have polynomial moments. Our bounds are computationally efficient for variational inference in that they require only standard values from variational objectives, straightforward analytic calculations, and simple Monte Carlo estimates. We show that our analysis naturally leads to a new and improved workflow for variational inference. Finally, we demonstrate the utility of our proposed workflow and error bounds on a real-data example with a widely used multilevel hierarchical model.

LR-GLM: High-Dimensional Bayesian Inference Using Low-Rank Data Approximations

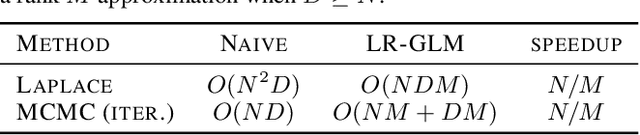
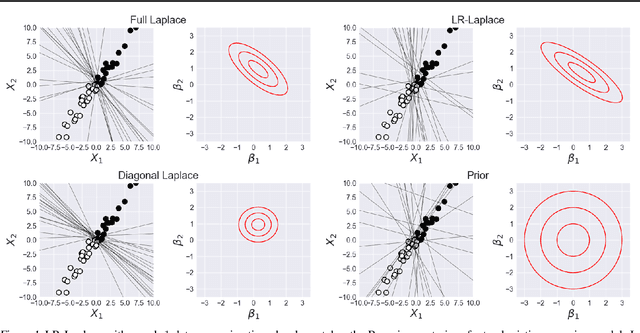
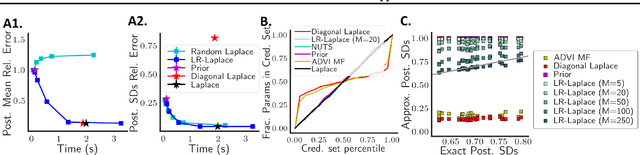
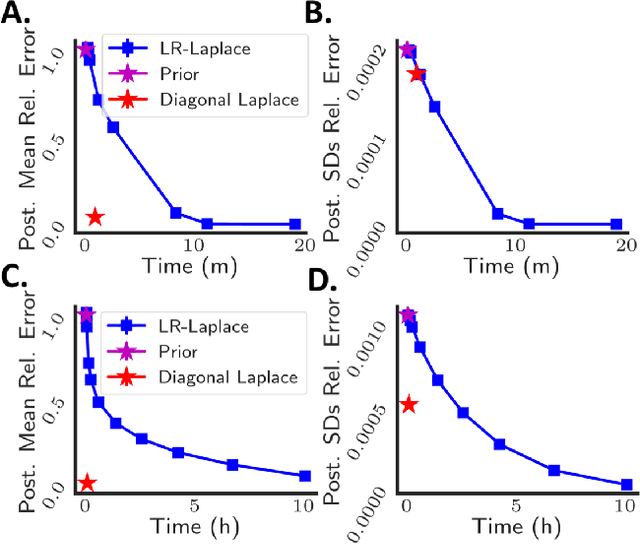
Due to the ease of modern data collection, applied statisticians often have access to a large set of covariates that they wish to relate to some observed outcome. Generalized linear models (GLMs) offer a particularly interpretable framework for such an analysis. In these high-dimensional problems, the number of covariates is often large relative to the number of observations, so we face non-trivial inferential uncertainty; a Bayesian approach allows coherent quantification of this uncertainty. Unfortunately, existing methods for Bayesian inference in GLMs require running times roughly cubic in parameter dimension, and so are limited to settings with at most tens of thousand parameters. We propose to reduce time and memory costs with a low-rank approximation of the data in an approach we call LR-GLM. When used with the Laplace approximation or Markov chain Monte Carlo, LR-GLM provides a full Bayesian posterior approximation and admits running times reduced by a full factor of the parameter dimension. We rigorously establish the quality of our approximation and show how the choice of rank allows a tunable computational-statistical trade-off. Experiments support our theory and demonstrate the efficacy of LR-GLM on real large-scale datasets.

The Kernel Interaction Trick: Fast Bayesian Discovery of Pairwise Interactions in High Dimensions

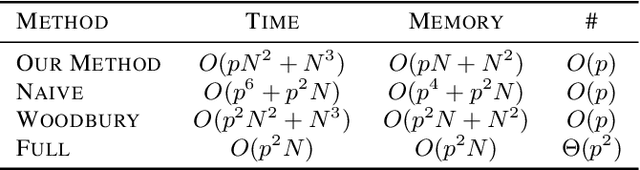
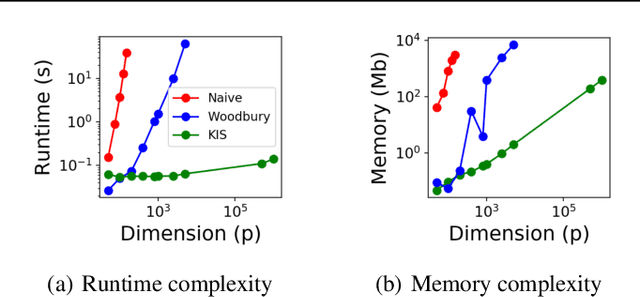
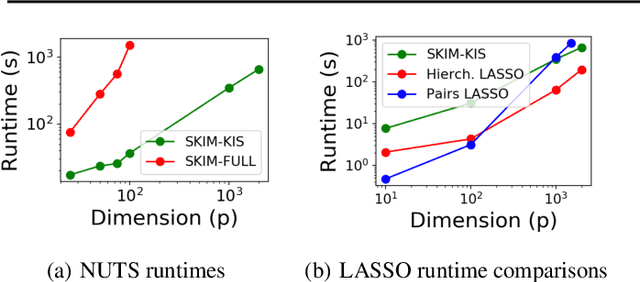
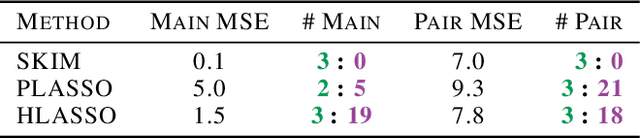
Discovering interaction effects on a response of interest is a fundamental problem faced in biology, medicine, economics, and many other scientific disciplines. In theory, Bayesian methods for discovering pairwise interactions enjoy many benefits such as coherent uncertainty quantification, the ability to incorporate background knowledge, and desirable shrinkage properties. In practice, however, Bayesian methods are often computationally intractable for even moderate-dimensional problems. Our key insight is that many hierarchical models of practical interest admit a particular Gaussian process (GP) representation; the GP allows us to capture the posterior with a vector of O(p) kernel hyper-parameters rather than O(p^2) interactions and main effects. With the implicit representation, we can run Markov chain Monte Carlo (MCMC) over model hyper-parameters in time and memory linear in p per iteration. We focus on sparsity-inducing models and show on datasets with a variety of covariate behaviors that our method: (1) reduces runtime by orders of magnitude over naive applications of MCMC, (2) provides lower Type I and Type II error relative to state-of-the-art LASSO-based approaches, and (3) offers improved computational scaling in high dimensions relative to existing Bayesian and LASSO-based approaches.

Random Feature Stein Discrepancies

Computable Stein discrepancies have been deployed for a variety of applications, ranging from sampler selection in posterior inference to approximate Bayesian inference to goodness-of-fit testing. Existing convergence-determining Stein discrepancies admit strong theoretical guarantees but suffer from a computational cost that grows quadratically in the sample size. While linear-time Stein discrepancies have been proposed for goodness-of-fit testing, they exhibit avoidable degradations in testing power---even when power is explicitly optimized. To address these shortcomings, we introduce feature Stein discrepancies ($\Phi$SDs), a new family of quality measures that can be cheaply approximated using importance sampling. We show how to construct $\Phi$SDs that provably determine the convergence of a sample to its target and develop high-accuracy approximations---random $\Phi$SDs (R$\Phi$SDs)---which are computable in near-linear time. In our experiments with sampler selection for approximate posterior inference and goodness-of-fit testing, R$\Phi$SDs perform as well or better than quadratic-time KSDs while being orders of magnitude faster to compute.