Heavy-Tailed Diffusion Models

Diffusion models achieve state-of-the-art generation quality across many applications, but their ability to capture rare or extreme events in heavy-tailed distributions remains unclear. In this work, we show that traditional diffusion and flow-matching models with standard Gaussian priors fail to capture heavy-tailed behavior. We address this by repurposing the diffusion framework for heavy-tail estimation using multivariate Student-t distributions. We develop a tailored perturbation kernel and derive the denoising posterior based on the conditional Student-t distribution for the backward process. Inspired by $\gamma$-divergence for heavy-tailed distributions, we derive a training objective for heavy-tailed denoisers. The resulting framework introduces controllable tail generation using only a single scalar hyperparameter, making it easily tunable for diverse real-world distributions. As specific instantiations of our framework, we introduce t-EDM and t-Flow, extensions of existing diffusion and flow models that employ a Student-t prior. Remarkably, our approach is readily compatible with standard Gaussian diffusion models and requires only minimal code changes. Empirically, we show that our t-EDM and t-Flow outperform standard diffusion models in heavy-tail estimation on high-resolution weather datasets in which generating rare and extreme events is crucial.

Kilometer-Scale Convection Allowing Model Emulation using Generative Diffusion Modeling

Storm-scale convection-allowing models (CAMs) are an important tool for predicting the evolution of thunderstorms and mesoscale convective systems that result in damaging extreme weather. By explicitly resolving convective dynamics within the atmosphere they afford meteorologists the nuance needed to provide outlook on hazard. Deep learning models have thus far not proven skilful at km-scale atmospheric simulation, despite being competitive at coarser resolution with state-of-the-art global, medium-range weather forecasting. We present a generative diffusion model called StormCast, which emulates the high-resolution rapid refresh (HRRR) model-NOAA's state-of-the-art 3km operational CAM. StormCast autoregressively predicts 99 state variables at km scale using a 1-hour time step, with dense vertical resolution in the atmospheric boundary layer, conditioned on 26 synoptic variables. We present evidence of successfully learnt km-scale dynamics including competitive 1-6 hour forecast skill for composite radar reflectivity alongside physically realistic convective cluster evolution, moist updrafts, and cold pool morphology. StormCast predictions maintain realistic power spectra for multiple predicted variables across multi-hour forecasts. Together, these results establish the potential for autoregressive ML to emulate CAMs -- opening up new km-scale frontiers for regional ML weather prediction and future climate hazard dynamical downscaling.

Generative Data Assimilation of Sparse Weather Station Observations at Kilometer Scales

Data assimilation of observational data into full atmospheric states is essential for weather forecast model initialization. Recently, methods for deep generative data assimilation have been proposed which allow for using new input data without retraining the model. They could also dramatically accelerate the costly data assimilation process used in operational regional weather models. Here, in a central US testbed, we demonstrate the viability of score-based data assimilation in the context of realistically complex km-scale weather. We train an unconditional diffusion model to generate snapshots of a state-of-the-art km-scale analysis product, the High Resolution Rapid Refresh. Then, using score-based data assimilation to incorporate sparse weather station data, the model produces maps of precipitation and surface winds. The generated fields display physically plausible structures, such as gust fronts, and sensitivity tests confirm learnt physics through multivariate relationships. Preliminary skill analysis shows the approach already outperforms a naive baseline of the High-Resolution Rapid Refresh system itself. By incorporating observations from 40 weather stations, 10\% lower RMSEs on left-out stations are attained. Despite some lingering imperfections such as insufficiently disperse ensemble DA estimates, we find the results overall an encouraging proof of concept, and the first at km-scale. It is a ripe time to explore extensions that combine increasingly ambitious regional state generators with an increasing set of in situ, ground-based, and satellite remote sensing data streams.

Coupled Ocean-Atmosphere Dynamics in a Machine Learning Earth System Model

Seasonal climate forecasts are socioeconomically important for managing the impacts of extreme weather events and for planning in sectors like agriculture and energy. Climate predictability on seasonal timescales is tied to boundary effects of the ocean on the atmosphere and coupled interactions in the ocean-atmosphere system. We present the Ocean-linked-atmosphere (Ola) model, a high-resolution (0.25{\deg}) Artificial Intelligence/ Machine Learning (AI/ML) coupled earth-system model which separately models the ocean and atmosphere dynamics using an autoregressive Spherical Fourier Neural Operator architecture, with a view towards enabling fast, accurate, large ensemble forecasts on the seasonal timescale. We find that Ola exhibits learned characteristics of ocean-atmosphere coupled dynamics including tropical oceanic waves with appropriate phase speeds, and an internally generated El Ni\~no/Southern Oscillation (ENSO) having realistic amplitude, geographic structure, and vertical structure within the ocean mixed layer. We present initial evidence of skill in forecasting the ENSO which compares favorably to the SPEAR model of the Geophysical Fluid Dynamics Laboratory.

DiffObs: Generative Diffusion for Global Forecasting of Satellite Observations

This work presents an autoregressive generative diffusion model (DiffObs) to predict the global evolution of daily precipitation, trained on a satellite observational product, and assessed with domain-specific diagnostics. The model is trained to probabilistically forecast day-ahead precipitation. Nonetheless, it is stable for multi-month rollouts, which reveal a qualitatively realistic superposition of convectively coupled wave modes in the tropics. Cross-spectral analysis confirms successful generation of low frequency variations associated with the Madden--Julian oscillation, which regulates most subseasonal to seasonal predictability in the observed atmosphere, and convectively coupled moist Kelvin waves with approximately correct dispersion relationships. Despite secondary issues and biases, the results affirm the potential for a next generation of global diffusion models trained on increasingly sparse, and increasingly direct and differentiated observations of the world, for practical applications in subseasonal and climate prediction.

A Practical Probabilistic Benchmark for AI Weather Models

Since the weather is chaotic, forecasts aim to predict the distribution of future states rather than make a single prediction. Recently, multiple data driven weather models have emerged claiming breakthroughs in skill. However, these have mostly been benchmarked using deterministic skill scores, and little is known about their probabilistic skill. Unfortunately, it is hard to fairly compare AI weather models in a probabilistic sense, since variations in choice of ensemble initialization, definition of state, and noise injection methodology become confounding. Moreover, even obtaining ensemble forecast baselines is a substantial engineering challenge given the data volumes involved. We sidestep both problems by applying a decades-old idea -- lagged ensembles -- whereby an ensemble can be constructed from a moderately-sized library of deterministic forecasts. This allows the first parameter-free intercomparison of leading AI weather models' probabilistic skill against an operational baseline. The results reveal that two leading AI weather models, i.e. GraphCast and Pangu, are tied on the probabilistic CRPS metric even though the former outperforms the latter in deterministic scoring. We also reveal how multiple time-step loss functions, which many data-driven weather models have employed, are counter-productive: they improve deterministic metrics at the cost of increased dissipation, deteriorating probabilistic skill. This is confirmed through ablations applied to a spherical Fourier Neural Operator (SFNO) approach to AI weather forecasting. Separate SFNO ablations modulating effective resolution reveal it has a useful effect on ensemble dispersion relevant to achieving good ensemble calibration. We hope these and forthcoming insights from lagged ensembles can help guide the development of AI weather forecasts and have thus shared the diagnostic code.

Generative Residual Diffusion Modeling for Km-scale Atmospheric Downscaling

The state of the art for physical hazard prediction from weather and climate requires expensive km-scale numerical simulations driven by coarser resolution global inputs. Here, a km-scale downscaling diffusion model is presented as a cost effective alternative. The model is trained from a regional high-resolution weather model over Taiwan, and conditioned on ERA5 reanalysis data. To address the downscaling uncertainties, large resolution ratios (25km to 2km), different physics involved at different scales and predict channels that are not in the input data, we employ a two-step approach (\textit{ResDiff}) where a (UNet) regression predicts the mean in the first step and a diffusion model predicts the residual in the second step. \textit{ResDiff} exhibits encouraging skill in bulk RMSE and CRPS scores. The predicted spectra and distributions from ResDiff faithfully recover important power law relationships regulating damaging wind and rain extremes. Case studies of coherent weather phenomena reveal appropriate multivariate relationships reminiscent of learnt physics. This includes the sharp wind and temperature variations that co-locate with intense rainfall in a cold front, and the extreme winds and rainfall bands that surround the eyewall of typhoons. Some evidence of simultaneous bias correction is found. A first attempt at downscaling directly from an operational global forecast model successfully retains many of these benefits. The implication is that a new era of fully end-to-end, global-to-regional machine learning weather prediction is likely near at hand.

ClimSim: An open large-scale dataset for training high-resolution physics emulators in hybrid multi-scale climate simulators

Modern climate projections lack adequate spatial and temporal resolution due to computational constraints. A consequence is inaccurate and imprecise prediction of critical processes such as storms. Hybrid methods that combine physics with machine learning (ML) have introduced a new generation of higher fidelity climate simulators that can sidestep Moore's Law by outsourcing compute-hungry, short, high-resolution simulations to ML emulators. However, this hybrid ML-physics simulation approach requires domain-specific treatment and has been inaccessible to ML experts because of lack of training data and relevant, easy-to-use workflows. We present ClimSim, the largest-ever dataset designed for hybrid ML-physics research. It comprises multi-scale climate simulations, developed by a consortium of climate scientists and ML researchers. It consists of 5.7 billion pairs of multivariate input and output vectors that isolate the influence of locally-nested, high-resolution, high-fidelity physics on a host climate simulator's macro-scale physical state. The dataset is global in coverage, spans multiple years at high sampling frequency, and is designed such that resulting emulators are compatible with downstream coupling into operational climate simulators. We implement a range of deterministic and stochastic regression baselines to highlight the ML challenges and their scoring. The data (https://huggingface.co/datasets/LEAP/ClimSim_high-res) and code (https://leap-stc.github.io/ClimSim) are released openly to support the development of hybrid ML-physics and high-fidelity climate simulations for the benefit of science and society.

Spherical Fourier Neural Operators: Learning Stable Dynamics on the Sphere

Fourier Neural Operators (FNOs) have proven to be an efficient and effective method for resolution-independent operator learning in a broad variety of application areas across scientific machine learning. A key reason for their success is their ability to accurately model long-range dependencies in spatio-temporal data by learning global convolutions in a computationally efficient manner. To this end, FNOs rely on the discrete Fourier transform (DFT), however, DFTs cause visual and spectral artifacts as well as pronounced dissipation when learning operators in spherical coordinates since they incorrectly assume a flat geometry. To overcome this limitation, we generalize FNOs on the sphere, introducing Spherical FNOs (SFNOs) for learning operators on spherical geometries. We apply SFNOs to forecasting atmospheric dynamics, and demonstrate stable auto\-regressive rollouts for a year of simulated time (1,460 steps), while retaining physically plausible dynamics. The SFNO has important implications for machine learning-based simulation of climate dynamics that could eventually help accelerate our response to climate change.

FourCastNet: Accelerating Global High-Resolution Weather Forecasting using Adaptive Fourier Neural Operators

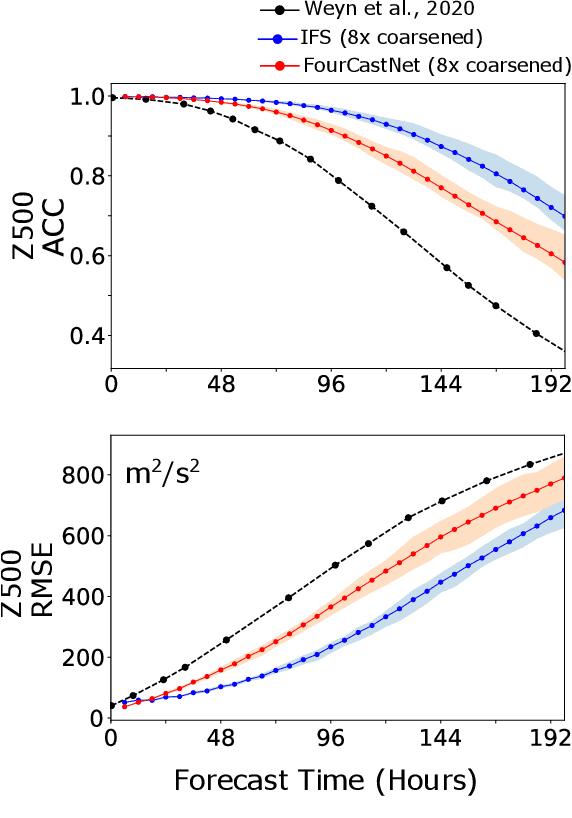
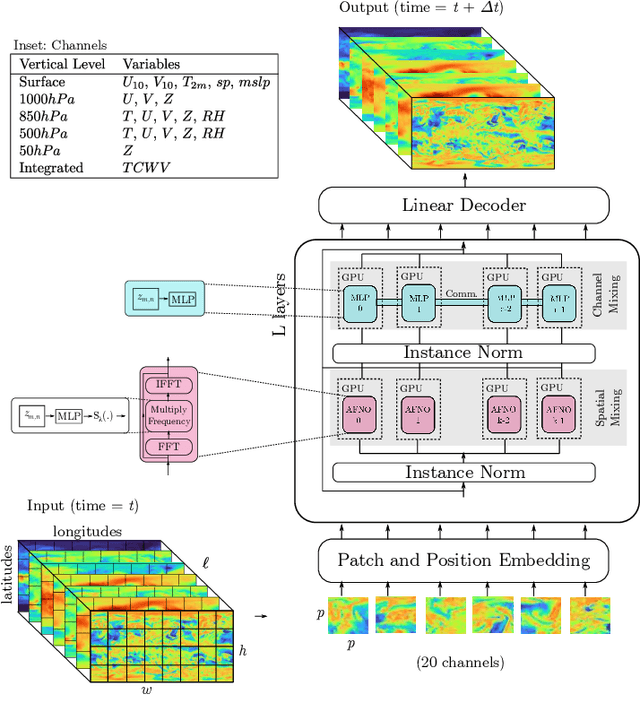
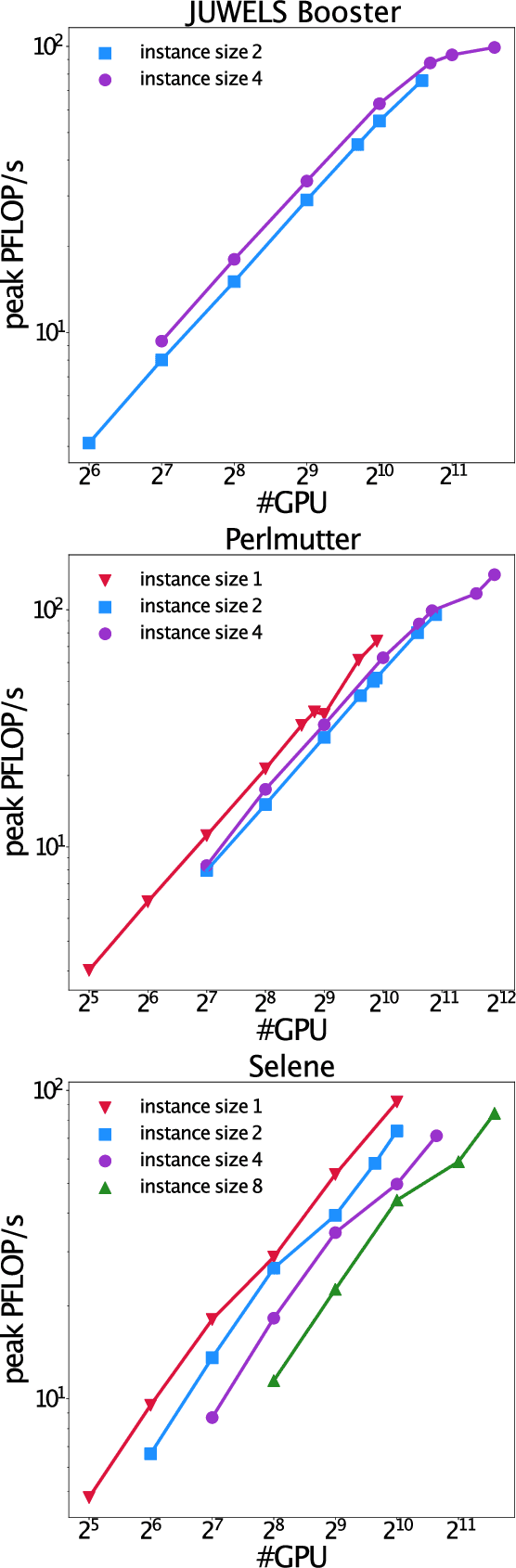
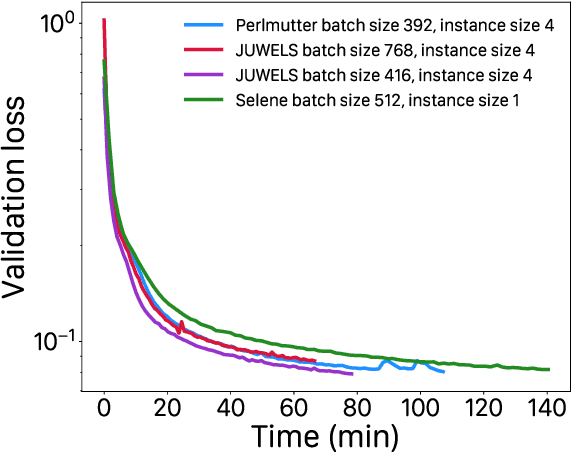
Extreme weather amplified by climate change is causing increasingly devastating impacts across the globe. The current use of physics-based numerical weather prediction (NWP) limits accuracy due to high computational cost and strict time-to-solution limits. We report that a data-driven deep learning Earth system emulator, FourCastNet, can predict global weather and generate medium-range forecasts five orders-of-magnitude faster than NWP while approaching state-of-the-art accuracy. FourCast-Net is optimized and scales efficiently on three supercomputing systems: Selene, Perlmutter, and JUWELS Booster up to 3,808 NVIDIA A100 GPUs, attaining 140.8 petaFLOPS in mixed precision (11.9%of peak at that scale). The time-to-solution for training FourCastNet measured on JUWELS Booster on 3,072GPUs is 67.4minutes, resulting in an 80,000times faster time-to-solution relative to state-of-the-art NWP, in inference. FourCastNet produces accurate instantaneous weather predictions for a week in advance, enables enormous ensembles that better capture weather extremes, and supports higher global forecast resolutions.