Joint Parameter and Parameterization Inference with Uncertainty Quantification through Differentiable Programming

Accurate representations of unknown and sub-grid physical processes through parameterizations (or closure) in numerical simulations with quantified uncertainty are critical for resolving the coarse-grained partial differential equations that govern many problems ranging from weather and climate prediction to turbulence simulations. Recent advances have seen machine learning (ML) increasingly applied to model these subgrid processes, resulting in the development of hybrid physics-ML models through the integration with numerical solvers. In this work, we introduce a novel framework for the joint estimation and uncertainty quantification of physical parameters and machine learning parameterizations in tandem, leveraging differentiable programming. Achieved through online training and efficient Bayesian inference within a high-dimensional parameter space, this approach is enabled by the capabilities of differentiable programming. This proof of concept underscores the substantial potential of differentiable programming in synergistically combining machine learning with differential equations, thereby enhancing the capabilities of hybrid physics-ML modeling.

Multi-fidelity climate model parameterization for better generalization and extrapolation

Machine-learning-based parameterizations (i.e. representation of sub-grid processes) of global climate models or turbulent simulations have recently been proposed as a powerful alternative to physical, but empirical, representations, offering a lower computational cost and higher accuracy. Yet, those approaches still suffer from a lack of generalization and extrapolation beyond the training data, which is however critical to projecting climate change or unobserved regimes of turbulence. Here we show that a multi-fidelity approach, which integrates datasets of different accuracy and abundance, can provide the best of both worlds: the capacity to extrapolate leveraging the physically-based parameterization and a higher accuracy using the machine-learning-based parameterizations. In an application to climate modeling, the multi-fidelity framework yields more accurate climate projections without requiring major increase in computational resources. Our multi-fidelity randomized prior networks (MF-RPNs) combine physical parameterization data as low-fidelity and storm-resolving historical run's data as high-fidelity. To extrapolate beyond the training data, the MF-RPNs are tested on high-fidelity warming scenarios, $+4K$, data. We show the MF-RPN's capacity to return much more skillful predictions compared to either low- or high-fidelity (historical data) simulations trained only on one regime while providing trustworthy uncertainty quantification across a wide range of scenarios. Our approach paves the way for the use of machine-learning based methods that can optimally leverage historical observations or high-fidelity simulations and extrapolate to unseen regimes such as climate change.

ClimSim: An open large-scale dataset for training high-resolution physics emulators in hybrid multi-scale climate simulators

Modern climate projections lack adequate spatial and temporal resolution due to computational constraints. A consequence is inaccurate and imprecise prediction of critical processes such as storms. Hybrid methods that combine physics with machine learning (ML) have introduced a new generation of higher fidelity climate simulators that can sidestep Moore's Law by outsourcing compute-hungry, short, high-resolution simulations to ML emulators. However, this hybrid ML-physics simulation approach requires domain-specific treatment and has been inaccessible to ML experts because of lack of training data and relevant, easy-to-use workflows. We present ClimSim, the largest-ever dataset designed for hybrid ML-physics research. It comprises multi-scale climate simulations, developed by a consortium of climate scientists and ML researchers. It consists of 5.7 billion pairs of multivariate input and output vectors that isolate the influence of locally-nested, high-resolution, high-fidelity physics on a host climate simulator's macro-scale physical state. The dataset is global in coverage, spans multiple years at high sampling frequency, and is designed such that resulting emulators are compatible with downstream coupling into operational climate simulators. We implement a range of deterministic and stochastic regression baselines to highlight the ML challenges and their scoring. The data (https://huggingface.co/datasets/LEAP/ClimSim_high-res) and code (https://leap-stc.github.io/ClimSim) are released openly to support the development of hybrid ML-physics and high-fidelity climate simulations for the benefit of science and society.

Scalable Bayesian optimization with high-dimensional outputs using randomized prior networks

Several fundamental problems in science and engineering consist of global optimization tasks involving unknown high-dimensional (black-box) functions that map a set of controllable variables to the outcomes of an expensive experiment. Bayesian Optimization (BO) techniques are known to be effective in tackling global optimization problems using a relatively small number objective function evaluations, but their performance suffers when dealing with high-dimensional outputs. To overcome the major challenge of dimensionality, here we propose a deep learning framework for BO and sequential decision making based on bootstrapped ensembles of neural architectures with randomized priors. Using appropriate architecture choices, we show that the proposed framework can approximate functional relationships between design variables and quantities of interest, even in cases where the latter take values in high-dimensional vector spaces or even infinite-dimensional function spaces. In the context of BO, we augmented the proposed probabilistic surrogates with re-parameterized Monte Carlo approximations of multiple-point (parallel) acquisition functions, as well as methodological extensions for accommodating black-box constraints and multi-fidelity information sources. We test the proposed framework against state-of-the-art methods for BO and demonstrate superior performance across several challenging tasks with high-dimensional outputs, including a constrained optimization task involving shape optimization of rotor blades in turbo-machinery.

History-Based, Bayesian, Closure for Stochastic Parameterization: Application to Lorenz '96

Physical parameterizations are used as representations of unresolved subgrid processes within weather and global climate models or coarse-scale turbulent models, whose resolutions are too coarse to resolve small-scale processes. These parameterizations are typically grounded on physically-based, yet empirical, representations of the underlying small-scale processes. Machine learning-based parameterizations have recently been proposed as an alternative and have shown great promises to reduce uncertainties associated with small-scale processes. Yet, those approaches still show some important mismatches that are often attributed to stochasticity in the considered process. This stochasticity can be due to noisy data, unresolved variables or simply to the inherent chaotic nature of the process. To address these issues, we develop a new type of parameterization (closure) which is based on a Bayesian formalism for neural networks, to account for uncertainty quantification, and includes memory, to account for the non-instantaneous response of the closure. To overcome the curse of dimensionality of Bayesian techniques in high-dimensional spaces, the Bayesian strategy is based on a Hamiltonian Monte Carlo Markov Chain sampling strategy that takes advantage of the likelihood function and kinetic energy's gradients with respect to the parameters to accelerate the sampling process. We apply the proposed Bayesian history-based parameterization to the Lorenz '96 model in the presence of noisy and sparse data, similar to satellite observations, and show its capacity to predict skillful forecasts of the resolved variables while returning trustworthy uncertainty quantifications for different sources of error. This approach paves the way for the use of Bayesian approaches for closure problems.

Fast PDE-constrained optimization via self-supervised operator learning

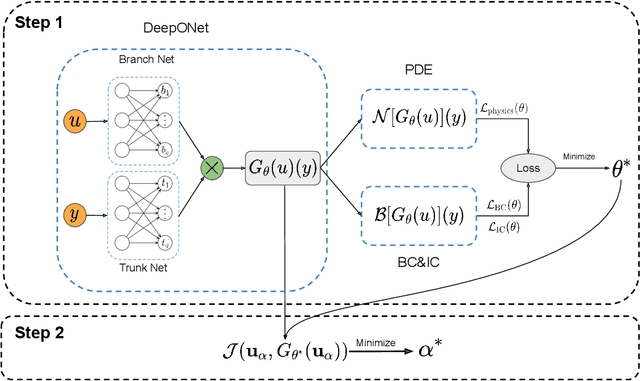
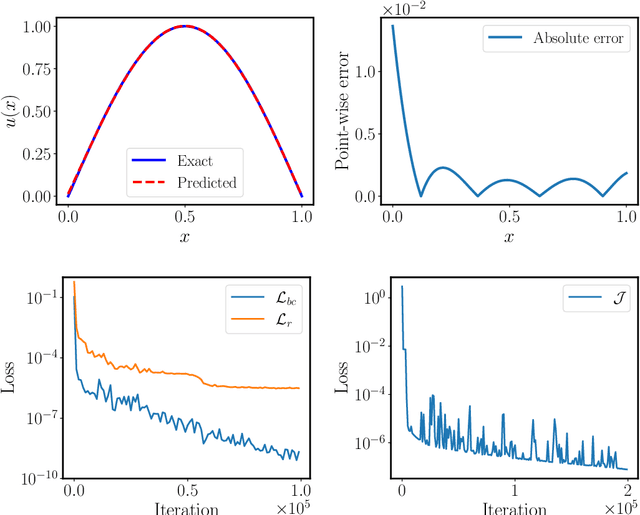
Design and optimal control problems are among the fundamental, ubiquitous tasks we face in science and engineering. In both cases, we aim to represent and optimize an unknown (black-box) function that associates a performance/outcome to a set of controllable variables through an experiment. In cases where the experimental dynamics can be described by partial differential equations (PDEs), such problems can be mathematically translated into PDE-constrained optimization tasks, which quickly become intractable as the number of control variables and the cost of experiments increases. In this work we leverage physics-informed deep operator networks (DeepONets) -- a self-supervised framework for learning the solution operator of parametric PDEs -- to build fast and differentiable surrogates for rapidly solving PDE-constrained optimization problems, even in the absence of any paired input-output training data. The effectiveness of the proposed framework will be demonstrated across different applications involving continuous functions as control or design variables, including time-dependent optimal control of heat transfer, and drag minimization of obstacles in Stokes flow. In all cases, we observe that DeepONets can minimize high-dimensional cost functionals in a matter of seconds, yielding a significant speed up compared to traditional adjoint PDE solvers that are typically costly and limited to relatively low-dimensional control/design parametrizations.

Gaussian processes meet NeuralODEs: A Bayesian framework for learning the dynamics of partially observed systems from scarce and noisy data

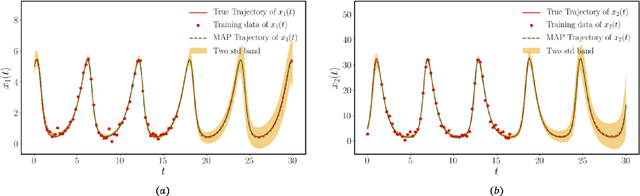
This paper presents a machine learning framework (GP-NODE) for Bayesian systems identification from partial, noisy and irregular observations of nonlinear dynamical systems. The proposed method takes advantage of recent developments in differentiable programming to propagate gradient information through ordinary differential equation solvers and perform Bayesian inference with respect to unknown model parameters using Hamiltonian Monte Carlo sampling and Gaussian Process priors over the observed system states. This allows us to exploit temporal correlations in the observed data, and efficiently infer posterior distributions over plausible models with quantified uncertainty. Moreover, the use of sparsity-promoting priors such as the Finnish Horseshoe for free model parameters enables the discovery of interpretable and parsimonious representations for the underlying latent dynamics. A series of numerical studies is presented to demonstrate the effectiveness of the proposed GP-NODE method including predator-prey systems, systems biology, and a 50-dimensional human motion dynamical system. Taken together, our findings put forth a novel, flexible and robust workflow for data-driven model discovery under uncertainty. All code and data accompanying this manuscript are available online at \url{https://github.com/PredictiveIntelligenceLab/GP-NODEs}.

Bayesian differential programming for robust systems identification under uncertainty

This paper presents a machine learning framework for Bayesian systems identification from noisy, sparse and irregular observations of nonlinear dynamical systems. The proposed method takes advantage of recent developments in differentiable programming to propagate gradient information through ordinary differential equation solvers and perform Bayesian inference with respect to unknown model parameters using Hamiltonian Monte Carlo. This allows us to efficiently infer posterior distributions over plausible models with quantified uncertainty, while the use of sparsity-promoting priors enables the discovery of interpretable and parsimonious representations for the underlying latent dynamics. A series of numerical studies is presented to demonstrate the effectiveness of the proposed methods including nonlinear oscillators, predator-prey systems, chaotic dynamics and systems biology. Taken all together, our findings put forth a novel, flexible and robust workflow for data-driven model discovery under uncertainty.