Transfer Regression via Pairwise Similarity Regularization

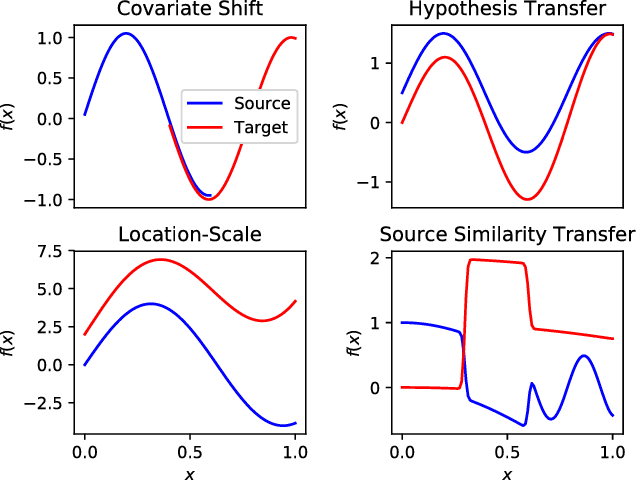
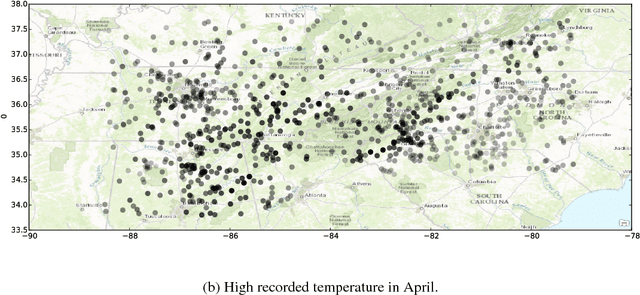
Transfer learning methods address the situation where little labeled training data from the "target" problem exists, but much training data from a related "source" domain is available. However, the overwhelming majority of transfer learning methods are designed for simple settings where the source and target predictive functions are almost identical, limiting the applicability of transfer learning methods to real world data. We propose a novel, weaker, property of the source domain that can be transferred even when the source and target predictive functions diverge. Our method assumes the source and target functions share a Pairwise Similarity property, where if the source function makes similar predictions on a pair of instances, then so will the target function. We propose Pairwise Similarity Regularization Transfer, a flexible graph-based regularization framework which can incorporate this modeling assumption into standard supervised learning algorithms. We show how users can encode domain knowledge into our regularizer in the form of spatial continuity, pairwise "similarity constraints" and how our method can be scaled to large data sets using the Nystrom approximation. Finally, we present positive and negative results on real and synthetic data sets and discuss when our Pairwise Similarity transfer assumption seems to hold in practice.

Dense Transformer Networks

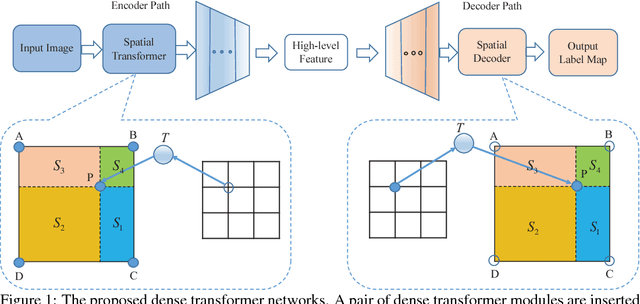
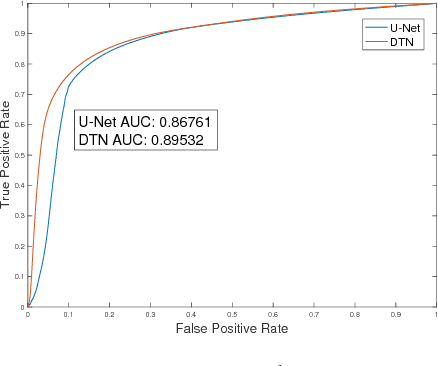
The key idea of current deep learning methods for dense prediction is to apply a model on a regular patch centered on each pixel to make pixel-wise predictions. These methods are limited in the sense that the patches are determined by network architecture instead of learned from data. In this work, we propose the dense transformer networks, which can learn the shapes and sizes of patches from data. The dense transformer networks employ an encoder-decoder architecture, and a pair of dense transformer modules are inserted into each of the encoder and decoder paths. The novelty of this work is that we provide technical solutions for learning the shapes and sizes of patches from data and efficiently restoring the spatial correspondence required for dense prediction. The proposed dense transformer modules are differentiable, thus the entire network can be trained. We apply the proposed networks on natural and biological image segmentation tasks and show superior performance is achieved in comparison to baseline methods.

Some Advances in Role Discovery in Graphs

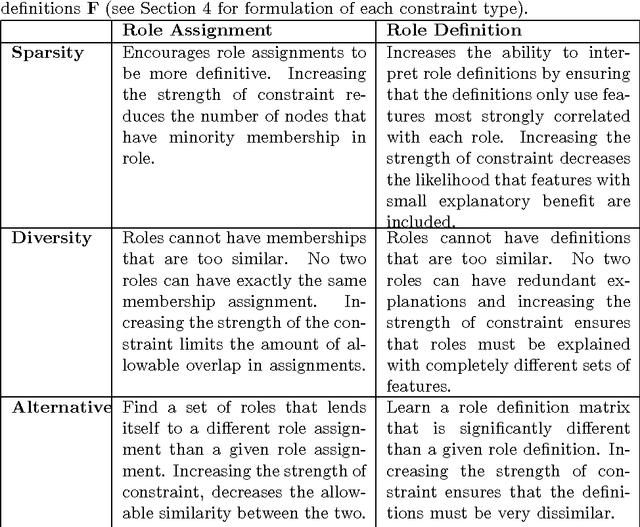
Role discovery in graphs is an emerging area that allows analysis of complex graphs in an intuitive way. In contrast to other graph prob- lems such as community discovery, which finds groups of highly connected nodes, the role discovery problem finds groups of nodes that share similar graph topological structure. However, existing work so far has two severe limitations that prevent its use in some domains. Firstly, it is completely unsupervised which is undesirable for a number of reasons. Secondly, most work is limited to a single relational graph. We address both these lim- itations in an intuitive and easy to implement alternating least squares framework. Our framework allows convex constraints to be placed on the role discovery problem which can provide useful supervision. In par- ticular we explore supervision to enforce i) sparsity, ii) diversity and iii) alternativeness. We then show how to lift this work for multi-relational graphs. A natural representation of a multi-relational graph is an order 3 tensor (rather than a matrix) and that a Tucker decomposition allows us to find complex interactions between collections of entities (E-groups) and the roles they play for a combination of relations (R-groups). Existing Tucker decomposition methods in tensor toolboxes are not suited for our purpose, so we create our own algorithm that we demonstrate is pragmatically useful.

Stochastic Coordinate Coding and Its Application for Drosophila Gene Expression Pattern Annotation

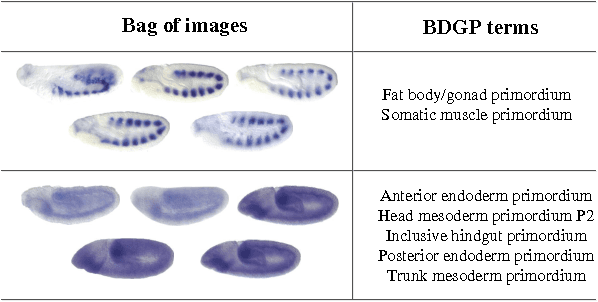
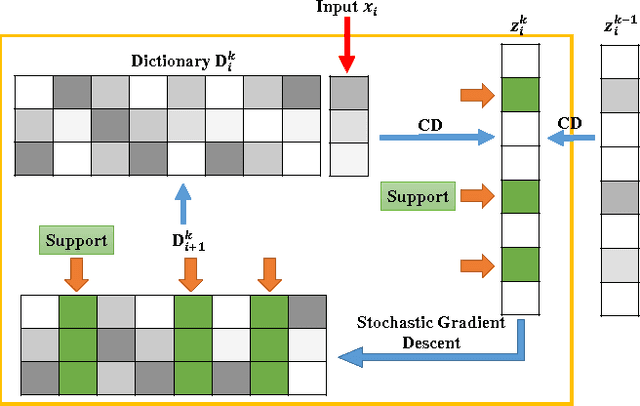
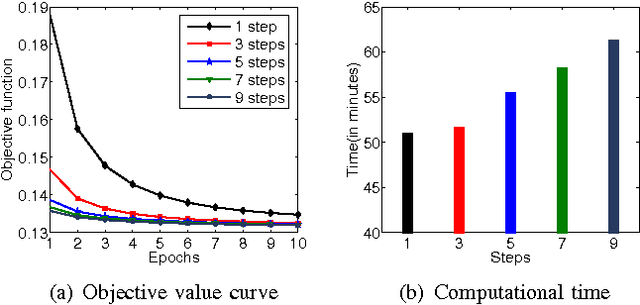
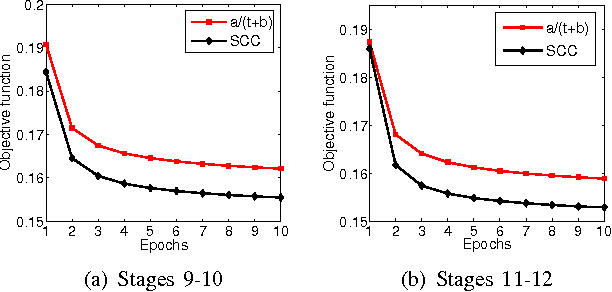
\textit{Drosophila melanogaster} has been established as a model organism for investigating the fundamental principles of developmental gene interactions. The gene expression patterns of \textit{Drosophila melanogaster} can be documented as digital images, which are annotated with anatomical ontology terms to facilitate pattern discovery and comparison. The automated annotation of gene expression pattern images has received increasing attention due to the recent expansion of the image database. The effectiveness of gene expression pattern annotation relies on the quality of feature representation. Previous studies have demonstrated that sparse coding is effective for extracting features from gene expression images. However, solving sparse coding remains a computationally challenging problem, especially when dealing with large-scale data sets and learning large size dictionaries. In this paper, we propose a novel algorithm to solve the sparse coding problem, called Stochastic Coordinate Coding (SCC). The proposed algorithm alternatively updates the sparse codes via just a few steps of coordinate descent and updates the dictionary via second order stochastic gradient descent. The computational cost is further reduced by focusing on the non-zero components of the sparse codes and the corresponding columns of the dictionary only in the updating procedure. Thus, the proposed algorithm significantly improves the efficiency and the scalability, making sparse coding applicable for large-scale data sets and large dictionary sizes. Our experiments on Drosophila gene expression data sets demonstrate the efficiency and the effectiveness of the proposed algorithm.

Minimum Message Length Clustering Using Gibbs Sampling

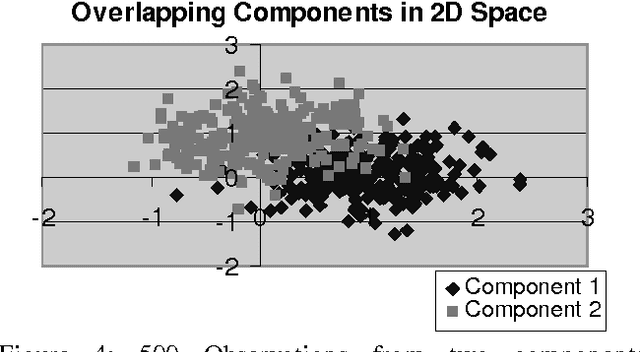
The K-Mean and EM algorithms are popular in clustering and mixture modeling, due to their simplicity and ease of implementation. However, they have several significant limitations. Both coverage to a local optimum of their respective objective functions (ignoring the uncertainty in the model space), require the apriori specification of the number of classes/clsuters, and are inconsistent. In this work we overcome these limitations by using the Minimum Message Length (MML) principle and a variation to the K-Means/EM observation assignment and parameter calculation scheme. We maintain the simplicity of these approaches while constructing a Bayesian mixture modeling tool that samples/searches the model space using a Markov Chain Monte Carlo (MCMC) sampler known as a Gibbs sampler. Gibbs sampling allows us to visit each model according to its posterior probability. Therefore, if the model space is multi-modal we will visit all models and not get stuck in local optima. We call our approach multiple chains at equilibrium (MCE) MML sampling.

On Constrained Spectral Clustering and Its Applications

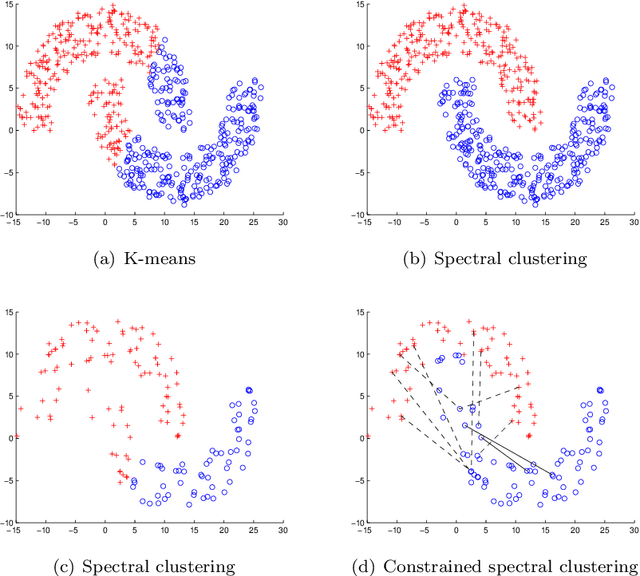
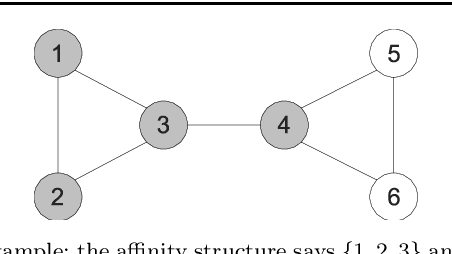
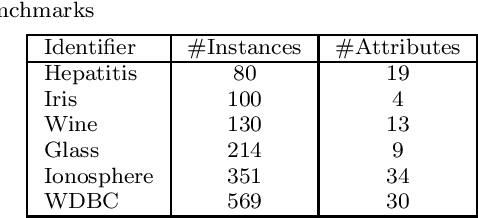
Constrained clustering has been well-studied for algorithms such as $K$-means and hierarchical clustering. However, how to satisfy many constraints in these algorithmic settings has been shown to be intractable. One alternative to encode many constraints is to use spectral clustering, which remains a developing area. In this paper, we propose a flexible framework for constrained spectral clustering. In contrast to some previous efforts that implicitly encode Must-Link and Cannot-Link constraints by modifying the graph Laplacian or constraining the underlying eigenspace, we present a more natural and principled formulation, which explicitly encodes the constraints as part of a constrained optimization problem. Our method offers several practical advantages: it can encode the degree of belief in Must-Link and Cannot-Link constraints; it guarantees to lower-bound how well the given constraints are satisfied using a user-specified threshold; it can be solved deterministically in polynomial time through generalized eigendecomposition. Furthermore, by inheriting the objective function from spectral clustering and encoding the constraints explicitly, much of the existing analysis of unconstrained spectral clustering techniques remains valid for our formulation. We validate the effectiveness of our approach by empirical results on both artificial and real datasets. We also demonstrate an innovative use of encoding large number of constraints: transfer learning via constraints.

A Reconstruction Error Formulation for Semi-Supervised Multi-task and Multi-view Learning

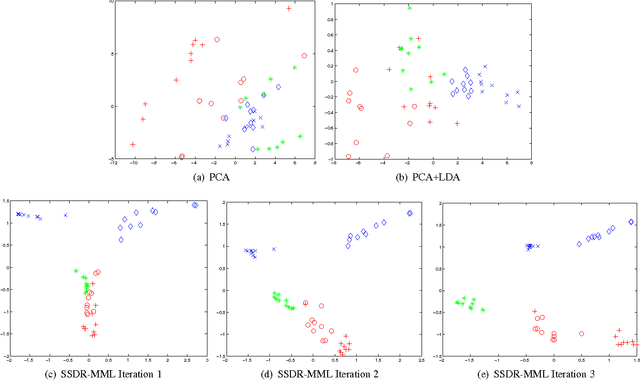
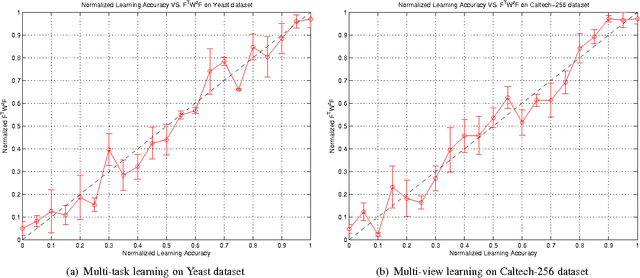
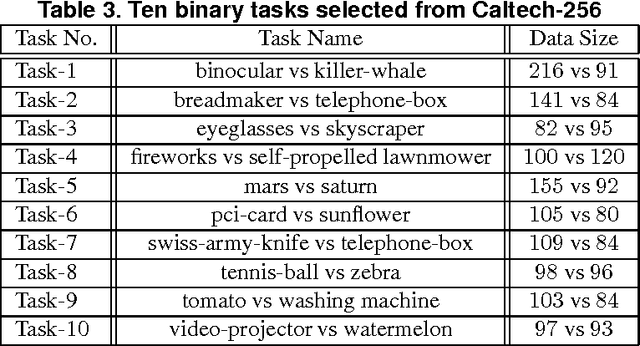
A significant challenge to make learning techniques more suitable for general purpose use is to move beyond i) complete supervision, ii) low dimensional data, iii) a single task and single view per instance. Solving these challenges allows working with "Big Data" problems that are typically high dimensional with multiple (but possibly incomplete) labelings and views. While other work has addressed each of these problems separately, in this paper we show how to address them together, namely semi-supervised dimension reduction for multi-task and multi-view learning (SSDR-MML), which performs optimization for dimension reduction and label inference in semi-supervised setting. The proposed framework is designed to handle both multi-task and multi-view learning settings, and can be easily adapted to many useful applications. Information obtained from all tasks and views is combined via reconstruction errors in a linear fashion that can be efficiently solved using an alternating optimization scheme. Our formulation has a number of advantages. We explicitly model the information combining mechanism as a data structure (a weight/nearest-neighbor matrix) which allows investigating fundamental questions in multi-task and multi-view learning. We address one such question by presenting a general measure to quantify the success of simultaneous learning of multiple tasks or from multiple views. We show that our SSDR-MML approach can outperform many state-of-the-art baseline methods and demonstrate the effectiveness of connecting dimension reduction and learning.