Aubrey Gress
Probabilistic Formulations of Regression with Mixed Guidance
Apr 01, 2018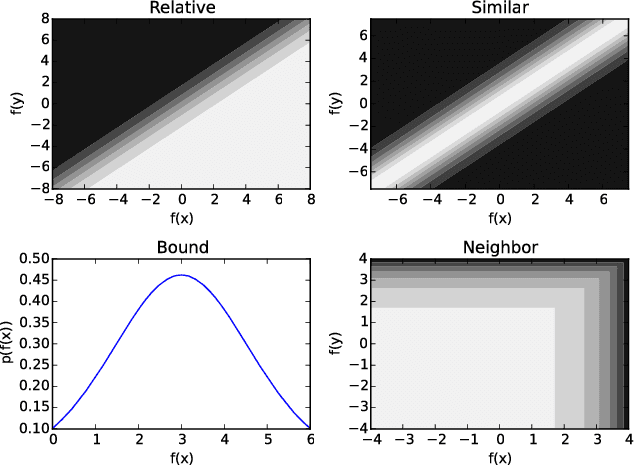
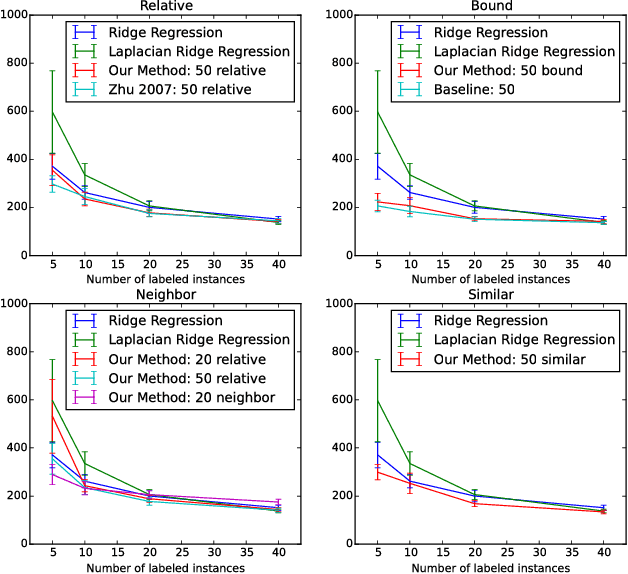
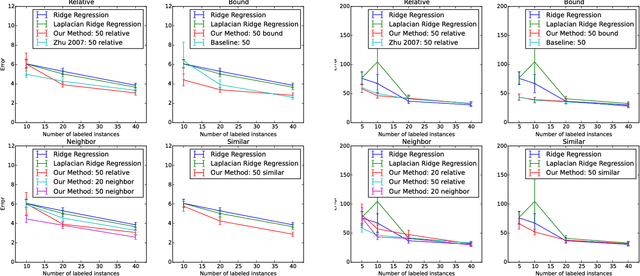
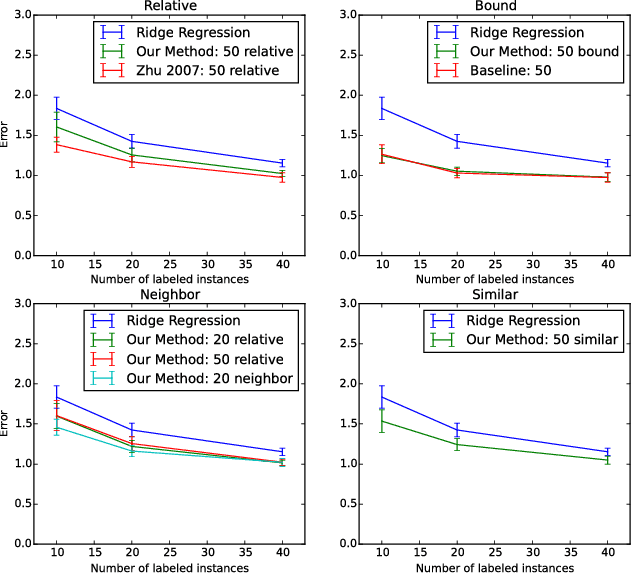
Abstract:Regression problems assume every instance is annotated (labeled) with a real value, a form of annotation we call \emph{strong guidance}. In order for these annotations to be accurate, they must be the result of a precise experiment or measurement. However, in some cases additional \emph{weak guidance} might be given by imprecise measurements, a domain expert or even crowd sourcing. Current formulations of regression are unable to use both types of guidance. We propose a regression framework that can also incorporate weak guidance based on relative orderings, bounds, neighboring and similarity relations. Consider learning to predict ages from portrait images, these new types of guidance allow weaker forms of guidance such as stating a person is in their 20s or two people are similar in age. These types of annotations can be easier to generate than strong guidance. We introduce a probabilistic formulation for these forms of weak guidance and show that the resulting optimization problems are convex. Our experimental results show the benefits of these formulations on several data sets.
Transfer Regression via Pairwise Similarity Regularization
Dec 23, 2017
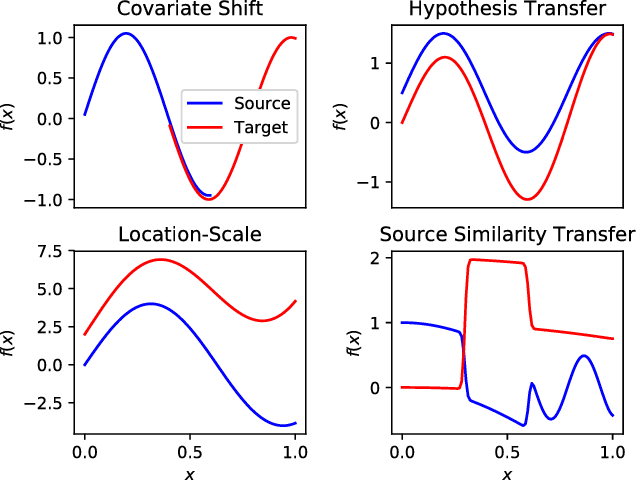

Abstract:Transfer learning methods address the situation where little labeled training data from the "target" problem exists, but much training data from a related "source" domain is available. However, the overwhelming majority of transfer learning methods are designed for simple settings where the source and target predictive functions are almost identical, limiting the applicability of transfer learning methods to real world data. We propose a novel, weaker, property of the source domain that can be transferred even when the source and target predictive functions diverge. Our method assumes the source and target functions share a Pairwise Similarity property, where if the source function makes similar predictions on a pair of instances, then so will the target function. We propose Pairwise Similarity Regularization Transfer, a flexible graph-based regularization framework which can incorporate this modeling assumption into standard supervised learning algorithms. We show how users can encode domain knowledge into our regularizer in the form of spatial continuity, pairwise "similarity constraints" and how our method can be scaled to large data sets using the Nystrom approximation. Finally, we present positive and negative results on real and synthetic data sets and discuss when our Pairwise Similarity transfer assumption seems to hold in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge