Chia-Tung Kuo
On The Equivalence of Tries and Dendrograms - Efficient Hierarchical Clustering of Traffic Data
Oct 12, 2018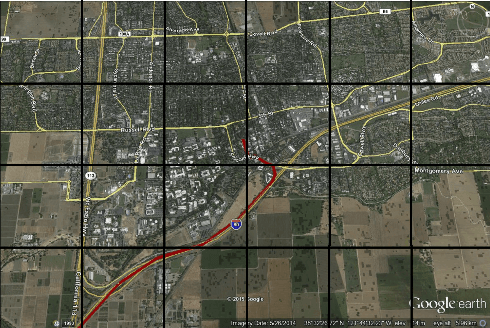
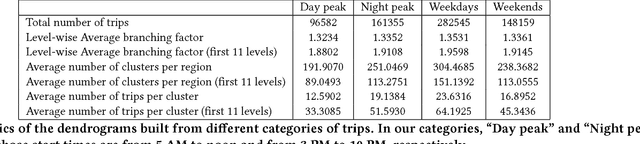
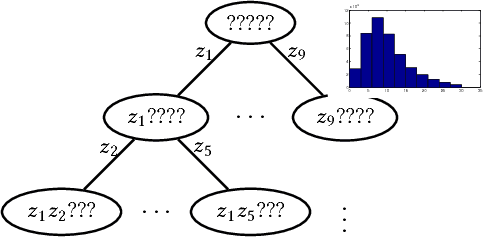

Abstract:The widespread use of GPS-enabled devices generates voluminous and continuous amounts of traffic data but analyzing such data for interpretable and actionable insights poses challenges. A hierarchical clustering of the trips has many uses such as discovering shortest paths, common routes and often traversed areas. However, hierarchical clustering typically has time complexity of $O(n^2 \log n)$ where $n$ is the number of instances, and is difficult to scale to large data sets associated with GPS data. Furthermore, incremental hierarchical clustering is still a developing area. Prefix trees (also called tries) can be efficiently constructed and updated in linear time (in $n$). We show how a specially constructed trie can compactly store the trips and further show this trie is equivalent to a dendrogram that would have been built by classic agglomerative hierarchical algorithms using a specific distance metric. This allows creating hierarchical clusterings of GPS trip data and updating this hierarchy in linear time. %we can extract a meaningful kernel and can also interpret the structure as clusterings of differing granularity as one progresses down the tree. We demonstrate the usefulness of our proposed approach on a real world data set of half a million taxis' GPS traces, well beyond the capabilities of agglomerative clustering methods. Our work is not limited to trip data and can be used with other data with a string representation.
Some Advances in Role Discovery in Graphs
Sep 09, 2016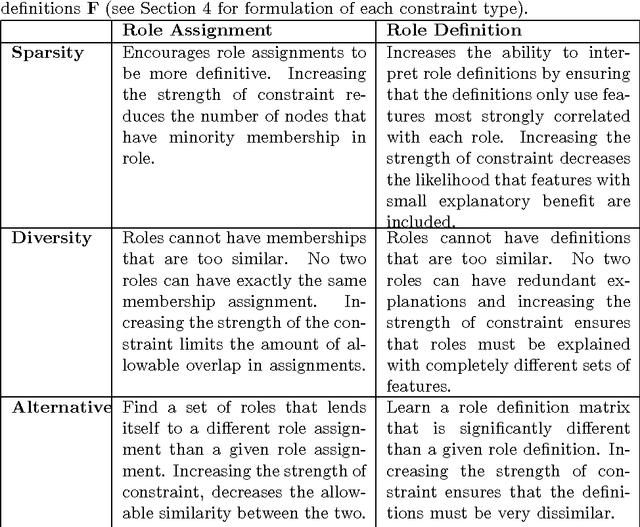

Abstract:Role discovery in graphs is an emerging area that allows analysis of complex graphs in an intuitive way. In contrast to other graph prob- lems such as community discovery, which finds groups of highly connected nodes, the role discovery problem finds groups of nodes that share similar graph topological structure. However, existing work so far has two severe limitations that prevent its use in some domains. Firstly, it is completely unsupervised which is undesirable for a number of reasons. Secondly, most work is limited to a single relational graph. We address both these lim- itations in an intuitive and easy to implement alternating least squares framework. Our framework allows convex constraints to be placed on the role discovery problem which can provide useful supervision. In par- ticular we explore supervision to enforce i) sparsity, ii) diversity and iii) alternativeness. We then show how to lift this work for multi-relational graphs. A natural representation of a multi-relational graph is an order 3 tensor (rather than a matrix) and that a Tucker decomposition allows us to find complex interactions between collections of entities (E-groups) and the roles they play for a combination of relations (R-groups). Existing Tucker decomposition methods in tensor toolboxes are not suited for our purpose, so we create our own algorithm that we demonstrate is pragmatically useful.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge