Holakou Rahmanian
HyperDPO: Hypernetwork-based Multi-Objective Fine-Tuning Framework
Oct 10, 2024



Abstract:In LLM alignment and many other ML applications, one often faces the Multi-Objective Fine-Tuning (MOFT) problem, i.e. fine-tuning an existing model with datasets labeled w.r.t. different objectives simultaneously. To address the challenge, we propose the HyperDPO framework, a hypernetwork-based approach that extends the Direct Preference Optimization (DPO) technique, originally developed for efficient LLM alignment with preference data, to accommodate the MOFT settings. By substituting the Bradley-Terry-Luce model in DPO with the Plackett-Luce model, our framework is capable of handling a wide range of MOFT tasks that involve listwise ranking datasets. Compared with previous approaches, HyperDPO enjoys an efficient one-shot training process for profiling the Pareto front of auxiliary objectives, and offers flexible post-training control over trade-offs. Additionally, we propose a novel Hyper Prompt Tuning design, that conveys continuous weight across objectives to transformer-based models without altering their architecture. We demonstrate the effectiveness and efficiency of the HyperDPO framework through its applications to various tasks, including Learning-to-Rank (LTR) and LLM alignment, highlighting its viability for large-scale ML deployments.
A Sinkhorn-type Algorithm for Constrained Optimal Transport
Mar 08, 2024



Abstract:Entropic optimal transport (OT) and the Sinkhorn algorithm have made it practical for machine learning practitioners to perform the fundamental task of calculating transport distance between statistical distributions. In this work, we focus on a general class of OT problems under a combination of equality and inequality constraints. We derive the corresponding entropy regularization formulation and introduce a Sinkhorn-type algorithm for such constrained OT problems supported by theoretical guarantees. We first bound the approximation error when solving the problem through entropic regularization, which reduces exponentially with the increase of the regularization parameter. Furthermore, we prove a sublinear first-order convergence rate of the proposed Sinkhorn-type algorithm in the dual space by characterizing the optimization procedure with a Lyapunov function. To achieve fast and higher-order convergence under weak entropy regularization, we augment the Sinkhorn-type algorithm with dynamic regularization scheduling and second-order acceleration. Overall, this work systematically combines recent theoretical and numerical advances in entropic optimal transport with the constrained case, allowing practitioners to derive approximate transport plans in complex scenarios.
Accelerating Sinkhorn Algorithm with Sparse Newton Iterations
Jan 20, 2024Abstract:Computing the optimal transport distance between statistical distributions is a fundamental task in machine learning. One remarkable recent advancement is entropic regularization and the Sinkhorn algorithm, which utilizes only matrix scaling and guarantees an approximated solution with near-linear runtime. Despite the success of the Sinkhorn algorithm, its runtime may still be slow due to the potentially large number of iterations needed for convergence. To achieve possibly super-exponential convergence, we present Sinkhorn-Newton-Sparse (SNS), an extension to the Sinkhorn algorithm, by introducing early stopping for the matrix scaling steps and a second stage featuring a Newton-type subroutine. Adopting the variational viewpoint that the Sinkhorn algorithm maximizes a concave Lyapunov potential, we offer the insight that the Hessian matrix of the potential function is approximately sparse. Sparsification of the Hessian results in a fast $O(n^2)$ per-iteration complexity, the same as the Sinkhorn algorithm. In terms of total iteration count, we observe that the SNS algorithm converges orders of magnitude faster across a wide range of practical cases, including optimal transportation between empirical distributions and calculating the Wasserstein $W_1, W_2$ distance of discretized densities. The empirical performance is corroborated by a rigorous bound on the approximate sparsity of the Hessian matrix.
Multi-Objective Optimization via Wasserstein-Fisher-Rao Gradient Flow
Nov 22, 2023



Abstract:Multi-objective optimization (MOO) aims to optimize multiple, possibly conflicting objectives with widespread applications. We introduce a novel interacting particle method for MOO inspired by molecular dynamics simulations. Our approach combines overdamped Langevin and birth-death dynamics, incorporating a "dominance potential" to steer particles toward global Pareto optimality. In contrast to previous methods, our method is able to relocate dominated particles, making it particularly adept at managing Pareto fronts of complicated geometries. Our method is also theoretically grounded as a Wasserstein-Fisher-Rao gradient flow with convergence guarantees. Extensive experiments confirm that our approach outperforms state-of-the-art methods on challenging synthetic and real-world datasets.
Toward Understanding Privileged Features Distillation in Learning-to-Rank
Sep 19, 2022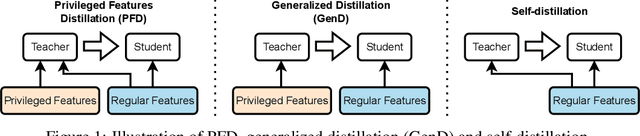
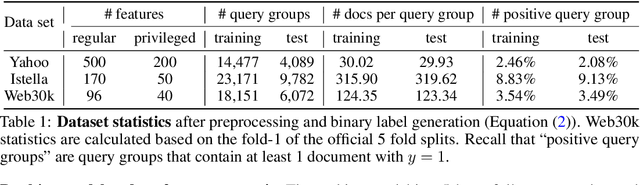
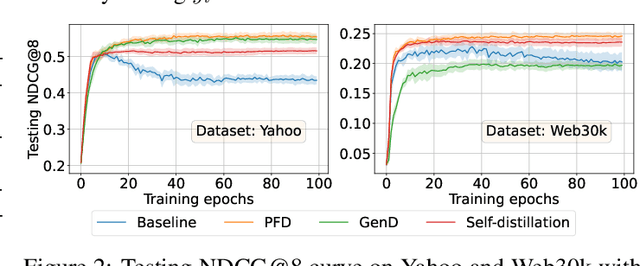
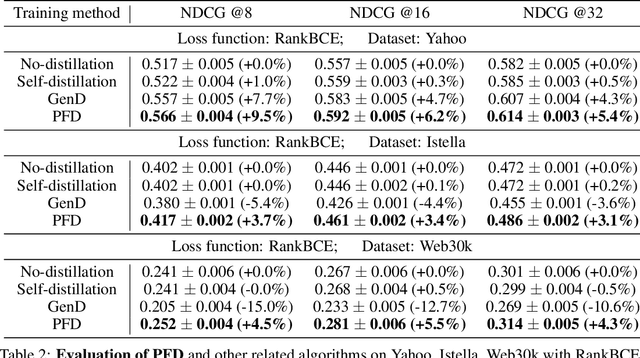
Abstract:In learning-to-rank problems, a privileged feature is one that is available during model training, but not available at test time. Such features naturally arise in merchandised recommendation systems; for instance, "user clicked this item" as a feature is predictive of "user purchased this item" in the offline data, but is clearly not available during online serving. Another source of privileged features is those that are too expensive to compute online but feasible to be added offline. Privileged features distillation (PFD) refers to a natural idea: train a "teacher" model using all features (including privileged ones) and then use it to train a "student" model that does not use the privileged features. In this paper, we first study PFD empirically on three public ranking datasets and an industrial-scale ranking problem derived from Amazon's logs. We show that PFD outperforms several baselines (no-distillation, pretraining-finetuning, self-distillation, and generalized distillation) on all these datasets. Next, we analyze why and when PFD performs well via both empirical ablation studies and theoretical analysis for linear models. Both investigations uncover an interesting non-monotone behavior: as the predictive power of a privileged feature increases, the performance of the resulting student model initially increases but then decreases. We show the reason for the later decreasing performance is that a very predictive privileged teacher produces predictions with high variance, which lead to high variance student estimates and inferior testing performance.
Online Non-Additive Path Learning under Full and Partial Information
Sep 18, 2018

Abstract:We study the problem of online path learning with non-additive gains, which is a central problem appearing in several applications, including ensemble structured prediction. We present new online algorithms for path learning with non-additive count-based gains for the three settings of full information, semi-bandit and full bandit. These algorithms admit very favorable regret guarantees and their guarantees can be viewed as the non-additive counterparts to the best known guarantees in the additive case. A key component of our algorithms is the definition and computation of an intermediate context-dependent automaton that enables us to use existing algorithms designed for additive gains. We further apply our methods to the important application of ensemble structured prediction. Finally, beyond count-based gains, we give an efficient implementation of the EXP3 algorithm for the full bandit setting with an arbitrary (non-additive) gain.
Online Dynamic Programming
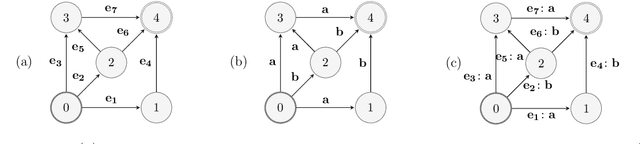
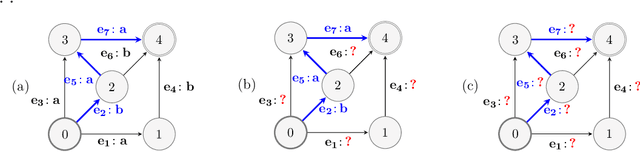
Dec 11, 2017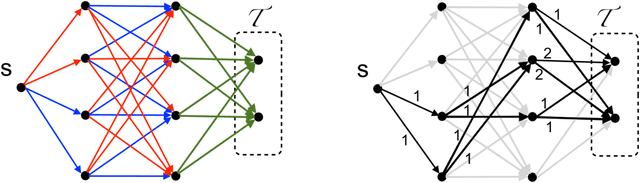
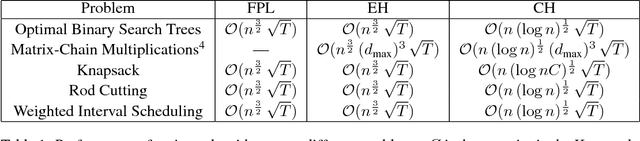
Abstract:We consider the problem of repeatedly solving a variant of the same dynamic programming problem in successive trials. An instance of the type of problems we consider is to find a good binary search tree in a changing environment.At the beginning of each trial, the learner probabilistically chooses a tree with the $n$ keys at the internal nodes and the $n+1$ gaps between keys at the leaves. The learner is then told the frequencies of the keys and gaps and is charged by the average search cost for the chosen tree. The problem is online because the frequencies can change between trials. The goal is to develop algorithms with the property that their total average search cost (loss) in all trials is close to the total loss of the best tree chosen in hindsight for all trials. The challenge, of course, is that the algorithm has to deal with exponential number of trees. We develop a general methodology for tackling such problems for a wide class of dynamic programming algorithms. Our framework allows us to extend online learning algorithms like Hedge and Component Hedge to a significantly wider class of combinatorial objects than was possible before.
Online Learning of Combinatorial Objects via Extended Formulation
Oct 30, 2017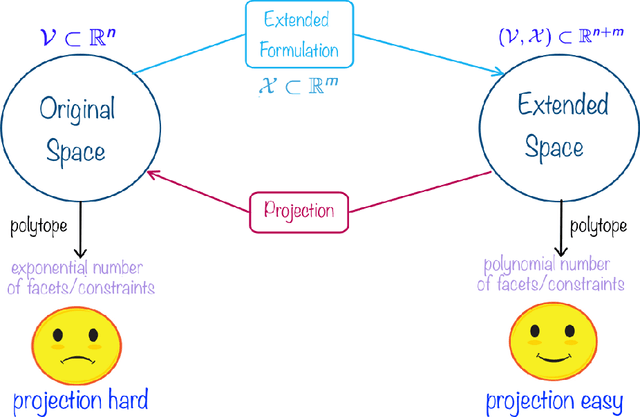
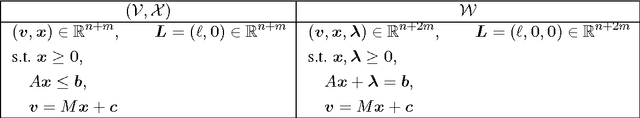
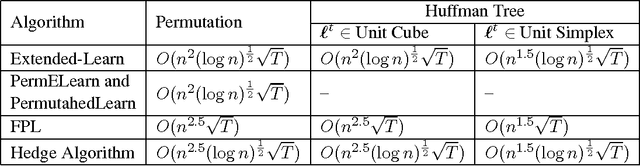
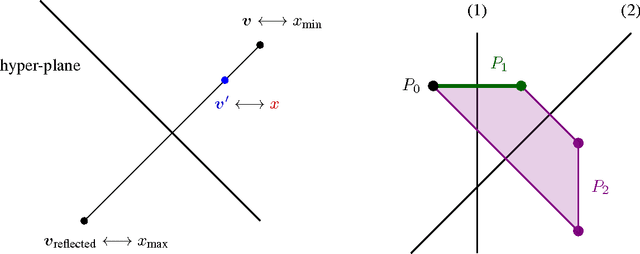
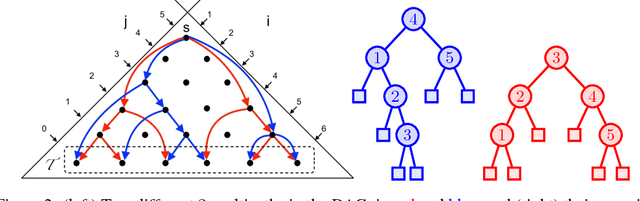
Abstract:The standard techniques for online learning of combinatorial objects perform multiplicative updates followed by projections into the convex hull of all the objects. However, this methodology can be expensive if the convex hull contains many facets. For example, the convex hull of $n$-symbol Huffman trees is known to have exponentially many facets (Maurras et al., 2010). We get around this difficulty by exploiting extended formulations (Kaibel, 2011), which encode the polytope of combinatorial objects in a higher dimensional "extended" space with only polynomially many facets. We develop a general framework for converting extended formulations into efficient online algorithms with good relative loss bounds. We present applications of our framework to online learning of Huffman trees and permutations. The regret bounds of the resulting algorithms are within a factor of $O(\sqrt{\log(n)})$ of the state-of-the-art specialized algorithms for permutations, and depending on the loss regimes, improve on or match the state-of-the-art for Huffman trees. Our method is general and can be applied to other combinatorial objects.
Deep Embedding Forest: Forest-based Serving with Deep Embedding Features
Mar 15, 2017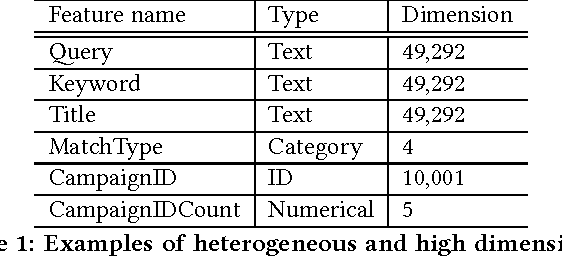
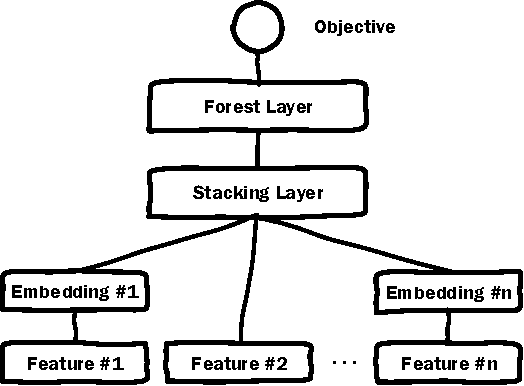
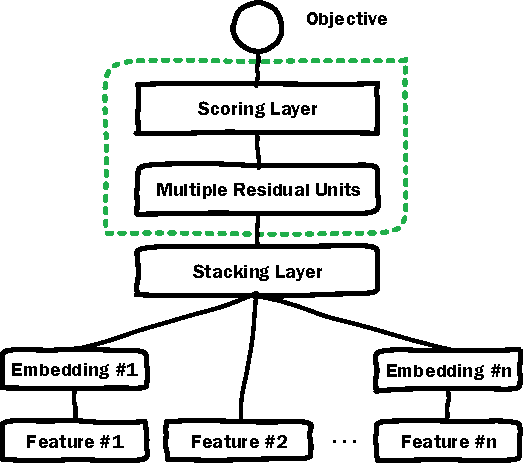

Abstract:Deep Neural Networks (DNN) have demonstrated superior ability to extract high level embedding vectors from low level features. Despite the success, the serving time is still the bottleneck due to expensive run-time computation of multiple layers of dense matrices. GPGPU, FPGA, or ASIC-based serving systems require additional hardware that are not in the mainstream design of most commercial applications. In contrast, tree or forest-based models are widely adopted because of low serving cost, but heavily depend on carefully engineered features. This work proposes a Deep Embedding Forest model that benefits from the best of both worlds. The model consists of a number of embedding layers and a forest/tree layer. The former maps high dimensional (hundreds of thousands to millions) and heterogeneous low-level features to the lower dimensional (thousands) vectors, and the latter ensures fast serving. Built on top of a representative DNN model called Deep Crossing, and two forest/tree-based models including XGBoost and LightGBM, a two-step Deep Embedding Forest algorithm is demonstrated to achieve on-par or slightly better performance as compared with the DNN counterpart, with only a fraction of serving time on conventional hardware. After comparing with a joint optimization algorithm called partial fuzzification, also proposed in this paper, it is concluded that the two-step Deep Embedding Forest has achieved near optimal performance. Experiments based on large scale data sets (up to 1 billion samples) from a major sponsored search engine proves the efficacy of the proposed model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge