Selective Matching Losses -- Not All Scores Are Created Equal

Learning systems match predicted scores to observations over some domain. Often, it is critical to produce accurate predictions in some subset (or region) of the domain, yet less important to accurately predict in other regions. We construct selective matching loss functions by design of increasing link functions over score domains. A matching loss is an integral over the link. A link defines loss sensitivity as function of the score, emphasizing high slope high sensitivity regions over flat ones. Loss asymmetry drives a model and resolves its underspecification to predict better in high sensitivity regions where it is more important, and to distinguish between high and low importance regions. A large variety of selective scalar losses can be designed with scaled and shifted Sigmoid and hyperbolic sine links. Their properties, however, do not extend to multi-class. Applying them per dimension lacks ranking sensitivity that assigns importance according to class score ranking. Utilizing composite Softmax functions, we develop a framework for multidimensional selective losses. We overcome limitations of the standard Softmax function, that is good for classification, but not for distinction between adjacent scores. Selective losses have substantial advantage over traditional losses in applications with more important score regions, including dwell-time prediction, retrieval, ranking with either pointwise, contrastive pairwise, or listwise losses, distillation problems, and fine-tuning alignment of Large Language Models (LLMs).

Noise misleads rotation invariant algorithms on sparse targets

It is well known that the class of rotation invariant algorithms are suboptimal even for learning sparse linear problems when the number of examples is below the "dimension" of the problem. This class includes any gradient descent trained neural net with a fully-connected input layer (initialized with a rotationally symmetric distribution). The simplest sparse problem is learning a single feature out of $d$ features. In that case the classification error or regression loss grows with $1-k/n$ where $k$ is the number of examples seen. These lower bounds become vacuous when the number of examples $k$ reaches the dimension $d$. We show that when noise is added to this sparse linear problem, rotation invariant algorithms are still suboptimal after seeing $d$ or more examples. We prove this via a lower bound for the Bayes optimal algorithm on a rotationally symmetrized problem. We then prove much lower upper bounds on the same problem for simple non-rotation invariant algorithms. Finally we analyze the gradient flow trajectories of many standard optimization algorithms in some simple cases and show how they veer toward or away from the sparse targets. We believe that our trajectory categorization will be useful in designing algorithms that can exploit sparse targets and our method for proving lower bounds will be crucial for analyzing other families of algorithms that admit different classes of invariances.

Tempered Calculus for ML: Application to Hyperbolic Model Embedding

Most mathematical distortions used in ML are fundamentally integral in nature: $f$-divergences, Bregman divergences, (regularized) optimal transport distances, integral probability metrics, geodesic distances, etc. In this paper, we unveil a grounded theory and tools which can help improve these distortions to better cope with ML requirements. We start with a generalization of Riemann integration that also encapsulates functions that are not strictly additive but are, more generally, $t$-additive, as in nonextensive statistical mechanics. Notably, this recovers Volterra's product integral as a special case. We then generalize the Fundamental Theorem of calculus using an extension of the (Euclidean) derivative. This, along with a series of more specific Theorems, serves as a basis for results showing how one can specifically design, alter, or change fundamental properties of distortion measures in a simple way, with a special emphasis on geometric- and ML-related properties that are the metricity, hyperbolicity, and encoding. We show how to apply it to a problem that has recently gained traction in ML: hyperbolic embeddings with a "cheap" and accurate encoding along the hyperbolic vs Euclidean scale. We unveil a new application for which the Poincar\'e disk model has very appealing features, and our theory comes in handy: \textit{model} embeddings for boosted combinations of decision trees, trained using the log-loss (trees) and logistic loss (combinations).

The Tempered Hilbert Simplex Distance and Its Application To Non-linear Embeddings of TEMs

Tempered Exponential Measures (TEMs) are a parametric generalization of the exponential family of distributions maximizing the tempered entropy function among positive measures subject to a probability normalization of their power densities. Calculus on TEMs relies on a deformed algebra of arithmetic operators induced by the deformed logarithms used to define the tempered entropy. In this work, we introduce three different parameterizations of finite discrete TEMs via Legendre functions of the negative tempered entropy function. In particular, we establish an isometry between such parameterizations in terms of a generalization of the Hilbert log cross-ratio simplex distance to a tempered Hilbert co-simplex distance. Similar to the Hilbert geometry, the tempered Hilbert distance is characterized as a $t$-symmetrization of the oriented tempered Funk distance. We motivate our construction by introducing the notion of $t$-lengths of smooth curves in a tautological Finsler manifold. We then demonstrate the properties of our generalized structure in different settings and numerically examine the quality of its differentiable approximations for optimization in machine learning settings.

Optimal Transport with Tempered Exponential Measures

In the field of optimal transport, two prominent subfields face each other: (i) unregularized optimal transport, ``\`a-la-Kantorovich'', which leads to extremely sparse plans but with algorithms that scale poorly, and (ii) entropic-regularized optimal transport, ``\`a-la-Sinkhorn-Cuturi'', which gets near-linear approximation algorithms but leads to maximally un-sparse plans. In this paper, we show that a generalization of the latter to tempered exponential measures, a generalization of exponential families with indirect measure normalization, gets to a very convenient middle ground, with both very fast approximation algorithms and sparsity which is under control up to sparsity patterns. In addition, it fits naturally in the unbalanced optimal transport problem setting as well.

Boosting with Tempered Exponential Measures

One of the most popular ML algorithms, AdaBoost, can be derived from the dual of a relative entropy minimization problem subject to the fact that the positive weights on the examples sum to one. Essentially, harder examples receive higher probabilities. We generalize this setup to the recently introduced {\it tempered exponential measure}s (TEMs) where normalization is enforced on a specific power of the measure and not the measure itself. TEMs are indexed by a parameter $t$ and generalize exponential families ($t=1$). Our algorithm, $t$-AdaBoost, recovers AdaBoost~as a special case ($t=1$). We show that $t$-AdaBoost retains AdaBoost's celebrated exponential convergence rate when $t\in [0,1)$ while allowing a slight improvement of the rate's hidden constant compared to $t=1$. $t$-AdaBoost partially computes on a generalization of classical arithmetic over the reals and brings notable properties like guaranteed bounded leveraging coefficients for $t\in [0,1)$. From the loss that $t$-AdaBoost minimizes (a generalization of the exponential loss), we show how to derive a new family of {\it tempered} losses for the induction of domain-partitioning classifiers like decision trees. Crucially, strict properness is ensured for all while their boosting rates span the full known spectrum. Experiments using $t$-AdaBoost+trees display that significant leverage can be achieved by tuning $t$.

A Mechanism for Sample-Efficient In-Context Learning for Sparse Retrieval Tasks

We study the phenomenon of \textit{in-context learning} (ICL) exhibited by large language models, where they can adapt to a new learning task, given a handful of labeled examples, without any explicit parameter optimization. Our goal is to explain how a pre-trained transformer model is able to perform ICL under reasonable assumptions on the pre-training process and the downstream tasks. We posit a mechanism whereby a transformer can achieve the following: (a) receive an i.i.d. sequence of examples which have been converted into a prompt using potentially-ambiguous delimiters, (b) correctly segment the prompt into examples and labels, (c) infer from the data a \textit{sparse linear regressor} hypothesis, and finally (d) apply this hypothesis on the given test example and return a predicted label. We establish that this entire procedure is implementable using the transformer mechanism, and we give sample complexity guarantees for this learning framework. Our empirical findings validate the challenge of segmentation, and we show a correspondence between our posited mechanisms and observed attention maps for step (c).

Layerwise Bregman Representation Learning with Applications to Knowledge Distillation

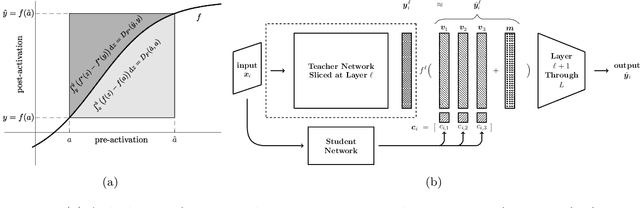
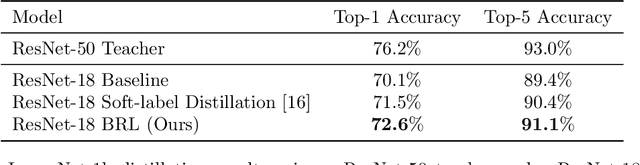
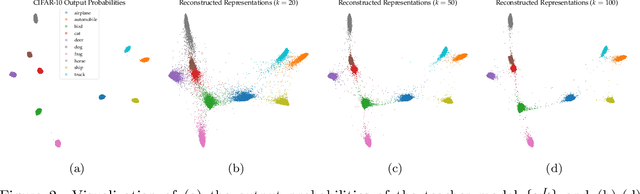
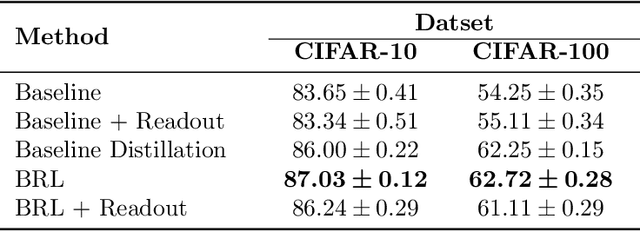
In this work, we propose a novel approach for layerwise representation learning of a trained neural network. In particular, we form a Bregman divergence based on the layer's transfer function and construct an extension of the original Bregman PCA formulation by incorporating a mean vector and normalizing the principal directions with respect to the geometry of the local convex function around the mean. This generalization allows exporting the learned representation as a fixed layer with a non-linearity. As an application to knowledge distillation, we cast the learning problem for the student network as predicting the compression coefficients of the teacher's representations, which are passed as the input to the imported layer. Our empirical findings indicate that our approach is substantially more effective for transferring information between networks than typical teacher-student training using the teacher's penultimate layer representations and soft labels.

Learning from Randomly Initialized Neural Network Features

We present the surprising result that randomly initialized neural networks are good feature extractors in expectation. These random features correspond to finite-sample realizations of what we call Neural Network Prior Kernel (NNPK), which is inherently infinite-dimensional. We conduct ablations across multiple architectures of varying sizes as well as initializations and activation functions. Our analysis suggests that certain structures that manifest in a trained model are already present at initialization. Therefore, NNPK may provide further insight into why neural networks are so effective in learning such structures.

Step-size Adaptation Using Exponentiated Gradient Updates

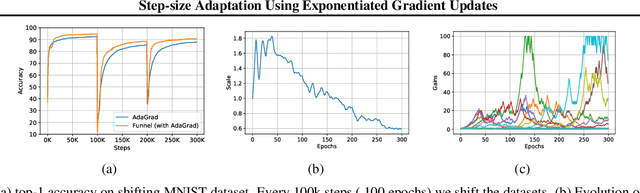
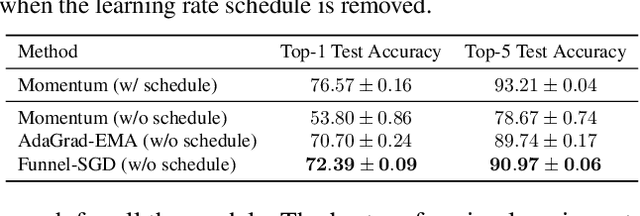
Optimizers like Adam and AdaGrad have been very successful in training large-scale neural networks. Yet, the performance of these methods is heavily dependent on a carefully tuned learning rate schedule. We show that in many large-scale applications, augmenting a given optimizer with an adaptive tuning method of the step-size greatly improves the performance. More precisely, we maintain a global step-size scale for the update as well as a gain factor for each coordinate. We adjust the global scale based on the alignment of the average gradient and the current gradient vectors. A similar approach is used for updating the local gain factors. This type of step-size scale tuning has been done before with gradient descent updates. In this paper, we update the step-size scale and the gain variables with exponentiated gradient updates instead. Experimentally, we show that our approach can achieve compelling accuracy on standard models without using any specially tuned learning rate schedule. We also show the effectiveness of our approach for quickly adapting to distribution shifts in the data during training.