Orbit: A Framework for Designing and Evaluating Multi-objective Rankers

Machine learning in production needs to balance multiple objectives: This is particularly evident in ranking or recommendation models, where conflicting objectives such as user engagement, satisfaction, diversity, and novelty must be considered at the same time. However, designing multi-objective rankers is inherently a dynamic wicked problem -- there is no single optimal solution, and the needs evolve over time. Effective design requires collaboration between cross-functional teams and careful analysis of a wide range of information. In this work, we introduce Orbit, a conceptual framework for Objective-centric Ranker Building and Iteration. The framework places objectives at the center of the design process, to serve as boundary objects for communication and guide practitioners for design and evaluation. We implement Orbit as an interactive system, which enables stakeholders to interact with objective spaces directly and supports real-time exploration and evaluation of design trade-offs. We evaluate Orbit through a user study involving twelve industry practitioners, showing that it supports efficient design space exploration, leads to more informed decision-making, and enhances awareness of the inherent trade-offs of multiple objectives. Orbit (1) opens up new opportunities of an objective-centric design process for any multi-objective ML models, as well as (2) sheds light on future designs that push practitioners to go beyond a narrow metric-centric or example-centric mindset.

HyperDPO: Hypernetwork-based Multi-Objective Fine-Tuning Framework

In LLM alignment and many other ML applications, one often faces the Multi-Objective Fine-Tuning (MOFT) problem, i.e. fine-tuning an existing model with datasets labeled w.r.t. different objectives simultaneously. To address the challenge, we propose the HyperDPO framework, a hypernetwork-based approach that extends the Direct Preference Optimization (DPO) technique, originally developed for efficient LLM alignment with preference data, to accommodate the MOFT settings. By substituting the Bradley-Terry-Luce model in DPO with the Plackett-Luce model, our framework is capable of handling a wide range of MOFT tasks that involve listwise ranking datasets. Compared with previous approaches, HyperDPO enjoys an efficient one-shot training process for profiling the Pareto front of auxiliary objectives, and offers flexible post-training control over trade-offs. Additionally, we propose a novel Hyper Prompt Tuning design, that conveys continuous weight across objectives to transformer-based models without altering their architecture. We demonstrate the effectiveness and efficiency of the HyperDPO framework through its applications to various tasks, including Learning-to-Rank (LTR) and LLM alignment, highlighting its viability for large-scale ML deployments.

A Sinkhorn-type Algorithm for Constrained Optimal Transport

Entropic optimal transport (OT) and the Sinkhorn algorithm have made it practical for machine learning practitioners to perform the fundamental task of calculating transport distance between statistical distributions. In this work, we focus on a general class of OT problems under a combination of equality and inequality constraints. We derive the corresponding entropy regularization formulation and introduce a Sinkhorn-type algorithm for such constrained OT problems supported by theoretical guarantees. We first bound the approximation error when solving the problem through entropic regularization, which reduces exponentially with the increase of the regularization parameter. Furthermore, we prove a sublinear first-order convergence rate of the proposed Sinkhorn-type algorithm in the dual space by characterizing the optimization procedure with a Lyapunov function. To achieve fast and higher-order convergence under weak entropy regularization, we augment the Sinkhorn-type algorithm with dynamic regularization scheduling and second-order acceleration. Overall, this work systematically combines recent theoretical and numerical advances in entropic optimal transport with the constrained case, allowing practitioners to derive approximate transport plans in complex scenarios.

Accelerating Sinkhorn Algorithm with Sparse Newton Iterations

Computing the optimal transport distance between statistical distributions is a fundamental task in machine learning. One remarkable recent advancement is entropic regularization and the Sinkhorn algorithm, which utilizes only matrix scaling and guarantees an approximated solution with near-linear runtime. Despite the success of the Sinkhorn algorithm, its runtime may still be slow due to the potentially large number of iterations needed for convergence. To achieve possibly super-exponential convergence, we present Sinkhorn-Newton-Sparse (SNS), an extension to the Sinkhorn algorithm, by introducing early stopping for the matrix scaling steps and a second stage featuring a Newton-type subroutine. Adopting the variational viewpoint that the Sinkhorn algorithm maximizes a concave Lyapunov potential, we offer the insight that the Hessian matrix of the potential function is approximately sparse. Sparsification of the Hessian results in a fast $O(n^2)$ per-iteration complexity, the same as the Sinkhorn algorithm. In terms of total iteration count, we observe that the SNS algorithm converges orders of magnitude faster across a wide range of practical cases, including optimal transportation between empirical distributions and calculating the Wasserstein $W_1, W_2$ distance of discretized densities. The empirical performance is corroborated by a rigorous bound on the approximate sparsity of the Hessian matrix.

Multi-Objective Optimization via Wasserstein-Fisher-Rao Gradient Flow

Multi-objective optimization (MOO) aims to optimize multiple, possibly conflicting objectives with widespread applications. We introduce a novel interacting particle method for MOO inspired by molecular dynamics simulations. Our approach combines overdamped Langevin and birth-death dynamics, incorporating a "dominance potential" to steer particles toward global Pareto optimality. In contrast to previous methods, our method is able to relocate dominated particles, making it particularly adept at managing Pareto fronts of complicated geometries. Our method is also theoretically grounded as a Wasserstein-Fisher-Rao gradient flow with convergence guarantees. Extensive experiments confirm that our approach outperforms state-of-the-art methods on challenging synthetic and real-world datasets.

Optimal Algorithms for Stochastic Bilevel Optimization under Relaxed Smoothness Conditions

Stochastic Bilevel optimization usually involves minimizing an upper-level (UL) function that is dependent on the arg-min of a strongly-convex lower-level (LL) function. Several algorithms utilize Neumann series to approximate certain matrix inverses involved in estimating the implicit gradient of the UL function (hypergradient). The state-of-the-art StOchastic Bilevel Algorithm (SOBA) [16] instead uses stochastic gradient descent steps to solve the linear system associated with the explicit matrix inversion. This modification enables SOBA to match the lower bound of sample complexity for the single-level counterpart in non-convex settings. Unfortunately, the current analysis of SOBA relies on the assumption of higher-order smoothness for the UL and LL functions to achieve optimality. In this paper, we introduce a novel fully single-loop and Hessian-inversion-free algorithmic framework for stochastic bilevel optimization and present a tighter analysis under standard smoothness assumptions (first-order Lipschitzness of the UL function and second-order Lipschitzness of the LL function). Furthermore, we show that by a slight modification of our approach, our algorithm can handle a more general multi-objective robust bilevel optimization problem. For this case, we obtain the state-of-the-art oracle complexity results demonstrating the generality of both the proposed algorithmic and analytic frameworks. Numerical experiments demonstrate the performance gain of the proposed algorithms over existing ones.

A One-Sample Decentralized Proximal Algorithm for Non-Convex Stochastic Composite Optimization

We focus on decentralized stochastic non-convex optimization, where $n$ agents work together to optimize a composite objective function which is a sum of a smooth term and a non-smooth convex term. To solve this problem, we propose two single-time scale algorithms: Prox-DASA and Prox-DASA-GT. These algorithms can find $\epsilon$-stationary points in $\mathcal{O}(n^{-1}\epsilon^{-2})$ iterations using constant batch sizes (i.e., $\mathcal{O}(1)$). Unlike prior work, our algorithms achieve a comparable complexity result without requiring large batch sizes, more complex per-iteration operations (such as double loops), or stronger assumptions. Our theoretical findings are supported by extensive numerical experiments, which demonstrate the superiority of our algorithms over previous approaches.

Field-wise Embedding Size Search via Structural Hard Auxiliary Mask Pruning for Click-Through Rate Prediction

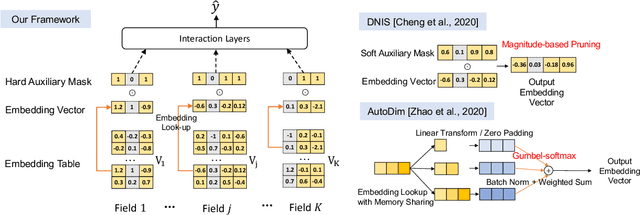
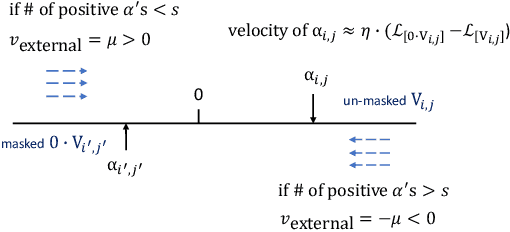
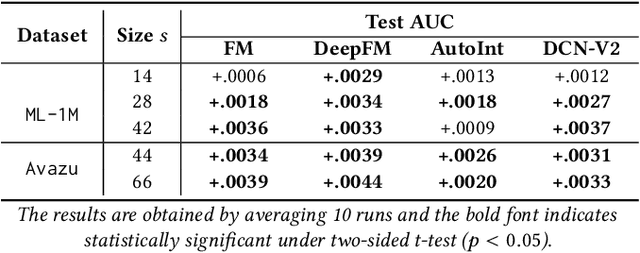
Feature embeddings are one of the most essential steps when training deep learning based Click-Through Rate prediction models, which map high-dimensional sparse features to dense embedding vectors. Classic human-crafted embedding size selection methods are shown to be "sub-optimal" in terms of the trade-off between memory usage and model capacity. The trending methods in Neural Architecture Search (NAS) have demonstrated their efficiency to search for embedding sizes. However, most existing NAS-based works suffer from expensive computational costs, the curse of dimensionality of the search space, and the discrepancy between continuous search space and discrete candidate space. Other works that prune embeddings in an unstructured manner fail to reduce the computational costs explicitly. In this paper, to address those limitations, we propose a novel strategy that searches for the optimal mixed-dimension embedding scheme by structurally pruning a super-net via Hard Auxiliary Mask. Our method aims to directly search candidate models in the discrete space using a simple and efficient gradient-based method. Furthermore, we introduce orthogonal regularity on embedding tables to reduce correlations within embedding columns and enhance representation capacity. Extensive experiments demonstrate it can effectively remove redundant embedding dimensions without great performance loss.

A Projection-free Algorithm for Constrained Stochastic Multi-level Composition Optimization

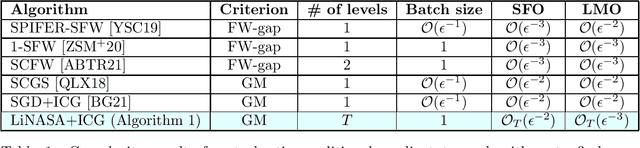
We propose a projection-free conditional gradient-type algorithm for smooth stochastic multi-level composition optimization, where the objective function is a nested composition of $T$ functions and the constraint set is a closed convex set. Our algorithm assumes access to noisy evaluations of the functions and their gradients, through a stochastic first-order oracle satisfying certain standard unbiasedness and second moment assumptions. We show that the number of calls to the stochastic first-order oracle and the linear-minimization oracle required by the proposed algorithm, to obtain an $\epsilon$-stationary solution, are of order $\mathcal{O}_T(\epsilon^{-2})$ and $\mathcal{O}_T(\epsilon^{-3})$ respectively, where $\mathcal{O}_T$ hides constants in $T$. Notably, the dependence of these complexity bounds on $\epsilon$ and $T$ are separate in the sense that changing one does not impact the dependence of the bounds on the other. Moreover, our algorithm is parameter-free and does not require any (increasing) order of mini-batches to converge unlike the common practice in the analysis of stochastic conditional gradient-type algorithms.

Statistical Inference for Polyak-Ruppert Averaged Zeroth-order Stochastic Gradient Algorithm

As machine learning models are deployed in critical applications, it becomes important to not just provide point estimators of the model parameters (or subsequent predictions), but also quantify the uncertainty associated with estimating the model parameters via confidence sets. In the last decade, estimating or training in several machine learning models has become synonymous with running stochastic gradient algorithms. However, computing the stochastic gradients in several settings is highly expensive or even impossible at times. An important question which has thus far not been addressed sufficiently in the statistical machine learning literature is that of equipping zeroth-order stochastic gradient algorithms with practical yet rigorous inferential capabilities. Towards this, in this work, we first establish a central limit theorem for Polyak-Ruppert averaged stochastic gradient algorithm in the zeroth-order setting. We then provide online estimators of the asymptotic covariance matrix appearing in the central limit theorem, thereby providing a practical procedure for constructing asymptotically valid confidence sets (or intervals) for parameter estimation (or prediction) in the zeroth-order setting.