MOLA: Enhancing Industrial Process Monitoring Using Multi-Block Orthogonal Long Short-Term Memory Autoencoder

In this work, we introduce MOLA: a Multi-block Orthogonal Long short-term memory Autoencoder paradigm, to conduct accurate, reliable fault detection of industrial processes. To achieve this, MOLA effectively extracts dynamic orthogonal features by introducing an orthogonality-based loss function to constrain the latent space output. This helps eliminate the redundancy in the features identified, thereby improving the overall monitoring performance. On top of this, a multi-block monitoring structure is proposed, which categorizes the process variables into multiple blocks by leveraging expert process knowledge about their associations with the overall process. Each block is associated with its specific Orthogonal Long short-term memory Autoencoder model, whose extracted dynamic orthogonal features are monitored by distance-based Hotelling's $T^2$ statistics and quantile-based cumulative sum (CUSUM) designed for multivariate data streams that are nonparametric, heterogeneous in nature. Compared to having a single model accounting for all process variables, such a multi-block structure improves the overall process monitoring performance significantly, especially for large-scale industrial processes. Finally, we propose an adaptive weight-based Bayesian fusion (W-BF) framework to aggregate all block-wise monitoring statistics into a global statistic that we monitor for faults, with the goal of improving fault detection speed by assigning weights to blocks based on the sequential order where alarms are raised. We demonstrate the efficiency and effectiveness of our MOLA framework by applying it to the Tennessee Eastman Process and comparing the performance with various benchmark methods.

A Sinkhorn-type Algorithm for Constrained Optimal Transport

Entropic optimal transport (OT) and the Sinkhorn algorithm have made it practical for machine learning practitioners to perform the fundamental task of calculating transport distance between statistical distributions. In this work, we focus on a general class of OT problems under a combination of equality and inequality constraints. We derive the corresponding entropy regularization formulation and introduce a Sinkhorn-type algorithm for such constrained OT problems supported by theoretical guarantees. We first bound the approximation error when solving the problem through entropic regularization, which reduces exponentially with the increase of the regularization parameter. Furthermore, we prove a sublinear first-order convergence rate of the proposed Sinkhorn-type algorithm in the dual space by characterizing the optimization procedure with a Lyapunov function. To achieve fast and higher-order convergence under weak entropy regularization, we augment the Sinkhorn-type algorithm with dynamic regularization scheduling and second-order acceleration. Overall, this work systematically combines recent theoretical and numerical advances in entropic optimal transport with the constrained case, allowing practitioners to derive approximate transport plans in complex scenarios.

Accelerating Sinkhorn Algorithm with Sparse Newton Iterations

Computing the optimal transport distance between statistical distributions is a fundamental task in machine learning. One remarkable recent advancement is entropic regularization and the Sinkhorn algorithm, which utilizes only matrix scaling and guarantees an approximated solution with near-linear runtime. Despite the success of the Sinkhorn algorithm, its runtime may still be slow due to the potentially large number of iterations needed for convergence. To achieve possibly super-exponential convergence, we present Sinkhorn-Newton-Sparse (SNS), an extension to the Sinkhorn algorithm, by introducing early stopping for the matrix scaling steps and a second stage featuring a Newton-type subroutine. Adopting the variational viewpoint that the Sinkhorn algorithm maximizes a concave Lyapunov potential, we offer the insight that the Hessian matrix of the potential function is approximately sparse. Sparsification of the Hessian results in a fast $O(n^2)$ per-iteration complexity, the same as the Sinkhorn algorithm. In terms of total iteration count, we observe that the SNS algorithm converges orders of magnitude faster across a wide range of practical cases, including optimal transportation between empirical distributions and calculating the Wasserstein $W_1, W_2$ distance of discretized densities. The empirical performance is corroborated by a rigorous bound on the approximate sparsity of the Hessian matrix.

Generative Modeling via Tree Tensor Network States

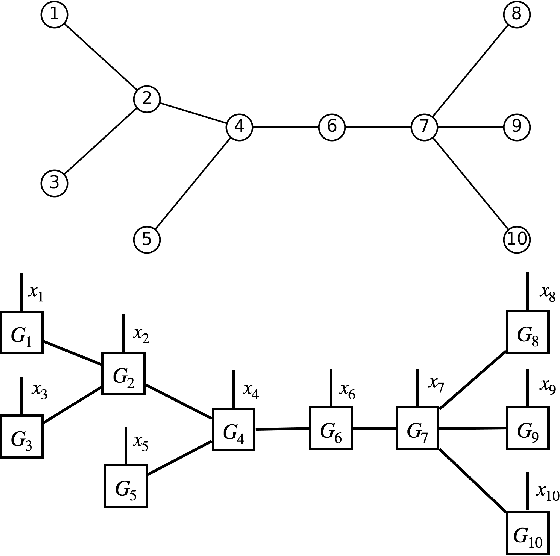
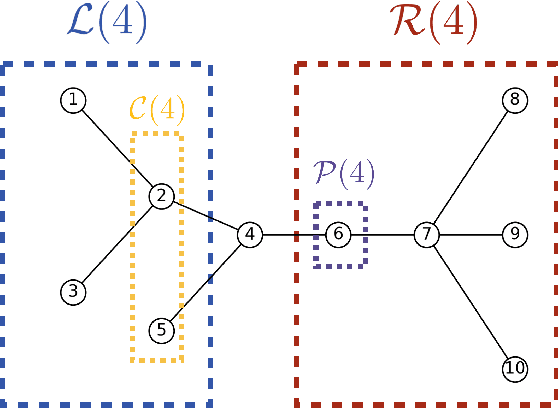
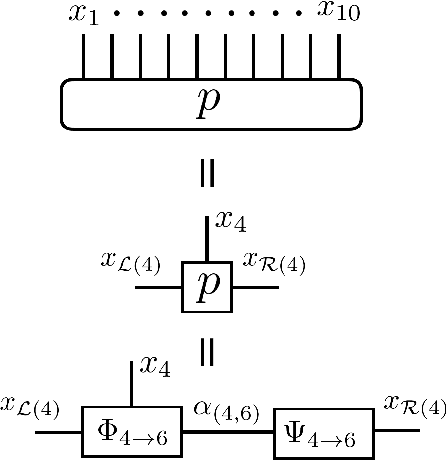
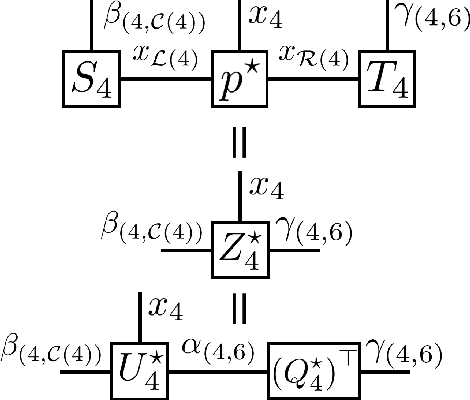
In this paper, we present a density estimation framework based on tree tensor-network states. The proposed method consists of determining the tree topology with Chow-Liu algorithm, and obtaining a linear system of equations that defines the tensor-network components via sketching techniques. Novel choices of sketch functions are developed in order to consider graphical models that contain loops. Sample complexity guarantees are provided and further corroborated by numerical experiments.

Operator Augmentation for Model-based Policy Evaluation

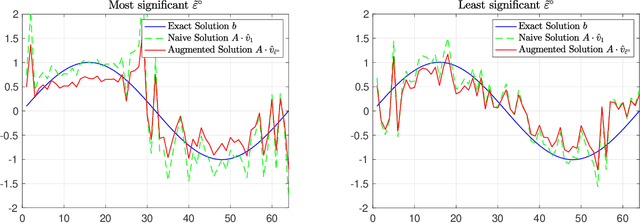
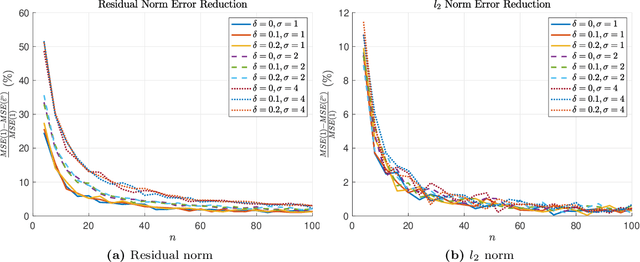
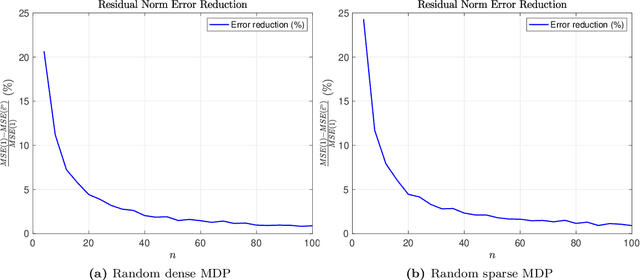
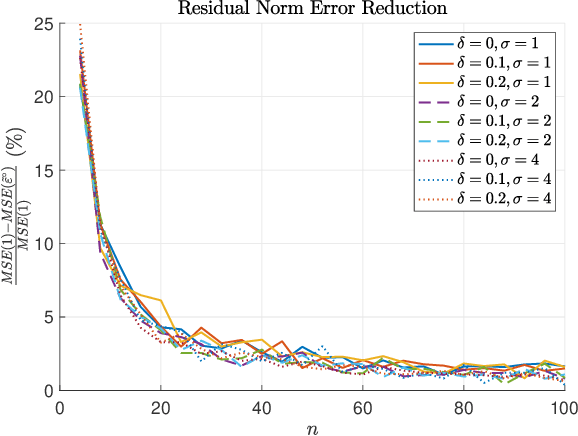
In model-based reinforcement learning, the transition matrix and reward vector are often estimated from random samples subject to noise. Even if the estimated model is an unbiased estimate of the true underlying model, the value function computed from the estimated model is biased. We introduce an operator augmentation method for reducing the error introduced by the estimated model. When the error is in the residual norm, we prove that the augmentation factor is always positive and upper bounded by $1 + O (1/n)$, where n is the number of samples used in learning each row of the transition matrix. We also propose a practical numerical algorithm for implementing the operator augmentation.