When Can Transformers Count to n?

Large language models based on the transformer architectures can solve highly complex tasks. But are there simple tasks that such models cannot solve? Here we focus on very simple counting tasks, that involve counting how many times a token in the vocabulary have appeared in a string. We show that if the dimension of the transformer state is linear in the context length, this task can be solved. However, the solution we propose does not scale beyond this limit, and we provide theoretical arguments for why it is likely impossible for a size limited transformer to implement this task. Our empirical results demonstrate the same phase-transition in performance, as anticipated by the theoretical argument. Our results demonstrate the importance of understanding how transformers can solve simple tasks.

Learning-Augmented Algorithms with Explicit Predictors

Recent advances in algorithmic design show how to utilize predictions obtained by machine learning models from past and present data. These approaches have demonstrated an enhancement in performance when the predictions are accurate, while also ensuring robustness by providing worst-case guarantees when predictions fail. In this paper we focus on online problems; prior research in this context was focused on a paradigm where the predictor is pre-trained on past data and then used as a black box (to get the predictions it was trained for). In contrast, in this work, we unpack the predictor and integrate the learning problem it gives rise for within the algorithmic challenge. In particular we allow the predictor to learn as it receives larger parts of the input, with the ultimate goal of designing online learning algorithms specifically tailored for the algorithmic task at hand. Adopting this perspective, we focus on a number of fundamental problems, including caching and scheduling, which have been well-studied in the black-box setting. For each of the problems we consider, we introduce new algorithms that take advantage of explicit learning algorithms which we carefully design towards optimizing the overall performance. We demonstrate the potential of our approach by deriving performance bounds which improve over those established in previous work.

On Differentially Private Online Predictions

In this work we introduce an interactive variant of joint differential privacy towards handling online processes in which existing privacy definitions seem too restrictive. We study basic properties of this definition and demonstrate that it satisfies (suitable variants) of group privacy, composition, and post processing. We then study the cost of interactive joint privacy in the basic setting of online classification. We show that any (possibly non-private) learning rule can be effectively transformed to a private learning rule with only a polynomial overhead in the mistake bound. This demonstrates a stark difference with more restrictive notions of privacy such as the one studied by Golowich and Livni (2021), where only a double exponential overhead on the mistake bound is known (via an information theoretic upper bound).

Concurrent Shuffle Differential Privacy Under Continual Observation

We introduce the concurrent shuffle model of differential privacy. In this model we have multiple concurrent shufflers permuting messages from different, possibly overlapping, batches of users. Similarly to the standard (single) shuffle model, the privacy requirement is that the concatenation of all shuffled messages should be differentially private. We study the private continual summation problem (a.k.a. the counter problem) and show that the concurrent shuffle model allows for significantly improved error compared to a standard (single) shuffle model. Specifically, we give a summation algorithm with error $\tilde{O}(n^{1/(2k+1)})$ with $k$ concurrent shufflers on a sequence of length $n$. Furthermore, we prove that this bound is tight for any $k$, even if the algorithm can choose the sizes of the batches adaptively. For $k=\log n$ shufflers, the resulting error is polylogarithmic, much better than $\tilde{\Theta}(n^{1/3})$ which we show is the smallest possible with a single shuffler. We use our online summation algorithm to get algorithms with improved regret bounds for the contextual linear bandit problem. In particular we get optimal $\tilde{O}(\sqrt{n})$ regret with $k= \tilde{\Omega}(\log n)$ concurrent shufflers.

Differentially-Private Bayes Consistency

We construct a universally Bayes consistent learning rule that satisfies differential privacy (DP). We first handle the setting of binary classification and then extend our rule to the more general setting of density estimation (with respect to the total variation metric). The existence of a universally consistent DP learner reveals a stark difference with the distribution-free PAC model. Indeed, in the latter DP learning is extremely limited: even one-dimensional linear classifiers are not privately learnable in this stringent model. Our result thus demonstrates that by allowing the learning rate to depend on the target distribution, one can circumvent the above-mentioned impossibility result and in fact, learn \emph{arbitrary} distributions by a single DP algorithm. As an application, we prove that any VC class can be privately learned in a semi-supervised setting with a near-optimal \emph{labeled} sample complexity of $\tilde{O}(d/\varepsilon)$ labeled examples (and with an unlabeled sample complexity that can depend on the target distribution).

Monotone Learning

The amount of training-data is one of the key factors which determines the generalization capacity of learning algorithms. Intuitively, one expects the error rate to decrease as the amount of training-data increases. Perhaps surprisingly, natural attempts to formalize this intuition give rise to interesting and challenging mathematical questions. For example, in their classical book on pattern recognition, Devroye, Gyorfi, and Lugosi (1996) ask whether there exists a {monotone} Bayes-consistent algorithm. This question remained open for over 25 years, until recently Pestov (2021) resolved it for binary classification, using an intricate construction of a monotone Bayes-consistent algorithm. We derive a general result in multiclass classification, showing that every learning algorithm A can be transformed to a monotone one with similar performance. Further, the transformation is efficient and only uses a black-box oracle access to A. This demonstrates that one can provably avoid non-monotonic behaviour without compromising performance, thus answering questions asked by Devroye et al (1996), Viering, Mey, and Loog (2019), Viering and Loog (2021), and by Mhammedi (2021). Our transformation readily implies monotone learners in a variety of contexts: for example it extends Pestov's result to classification tasks with an arbitrary number of labels. This is in contrast with Pestov's work which is tailored to binary classification. In addition, we provide uniform bounds on the error of the monotone algorithm. This makes our transformation applicable in distribution-free settings. For example, in PAC learning it implies that every learnable class admits a monotone PAC learner. This resolves questions by Viering, Mey, and Loog (2019); Viering and Loog (2021); Mhammedi (2021).

Differentially-Private Clustering of Easy Instances

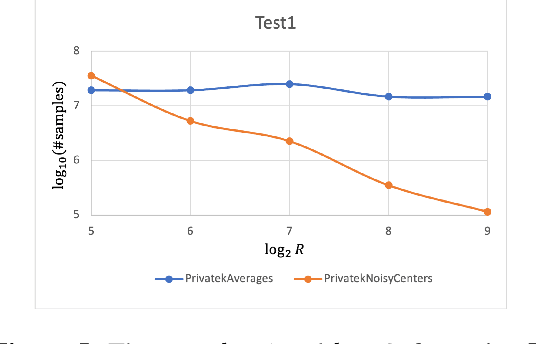
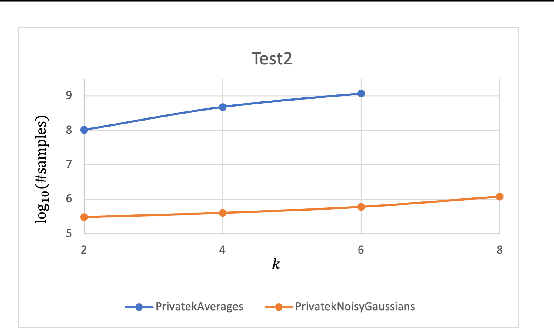
Clustering is a fundamental problem in data analysis. In differentially private clustering, the goal is to identify $k$ cluster centers without disclosing information on individual data points. Despite significant research progress, the problem had so far resisted practical solutions. In this work we aim at providing simple implementable differentially private clustering algorithms that provide utility when the data is "easy," e.g., when there exists a significant separation between the clusters. We propose a framework that allows us to apply non-private clustering algorithms to the easy instances and privately combine the results. We are able to get improved sample complexity bounds in some cases of Gaussian mixtures and $k$-means. We complement our theoretical analysis with an empirical evaluation on synthetic data.

FriendlyCore: Practical Differentially Private Aggregation

Differentially private algorithms for common metric aggregation tasks, such as clustering or averaging, often have limited practicality due to their complexity or a large number of data points that is required for accurate results. We propose a simple and practical tool $\mathsf{FriendlyCore}$ that takes a set of points ${\cal D}$ from an unrestricted (pseudo) metric space as input. When ${\cal D}$ has effective diameter $r$, $\mathsf{FriendlyCore}$ returns a "stable" subset ${\cal D}_G\subseteq {\cal D}$ that includes all points, except possibly few outliers, and is {\em certified} to have diameter $r$. $\mathsf{FriendlyCore}$ can be used to preprocess the input before privately aggregating it, potentially simplifying the aggregation or boosting its accuracy. Surprisingly, $\mathsf{FriendlyCore}$ is light-weight with no dependence on the dimension. We empirically demonstrate its advantages in boosting the accuracy of mean estimation, outperforming tailored methods.

Differentially Private Approximate Quantiles

In this work we study the problem of differentially private (DP) quantiles, in which given dataset $X$ and quantiles $q_1, ..., q_m \in [0,1]$, we want to output $m$ quantile estimations which are as close as possible to the true quantiles and preserve DP. We describe a simple recursive DP algorithm, which we call ApproximateQuantiles (AQ), for this task. We give a worst case upper bound on its error, and show that its error is much lower than of previous implementations on several different datasets. Furthermore, it gets this low error while running time two orders of magnitude faster that the best previous implementation.

Differentially Private Multi-Armed Bandits in the Shuffle Model

We give an $(\varepsilon,\delta)$-differentially private algorithm for the multi-armed bandit (MAB) problem in the shuffle model with a distribution-dependent regret of $O\left(\left(\sum_{a\in [k]:\Delta_a>0}\frac{\log T}{\Delta_a}\right)+\frac{k\sqrt{\log\frac{1}{\delta}}\log T}{\varepsilon}\right)$, and a distribution-independent regret of $O\left(\sqrt{kT\log T}+\frac{k\sqrt{\log\frac{1}{\delta}}\log T}{\varepsilon}\right)$, where $T$ is the number of rounds, $\Delta_a$ is the suboptimality gap of the arm $a$, and $k$ is the total number of arms. Our upper bound almost matches the regret of the best known algorithms for the centralized model, and significantly outperforms the best known algorithm in the local model.