Credit Attribution and Stable Compression

Credit attribution is crucial across various fields. In academic research, proper citation acknowledges prior work and establishes original contributions. Similarly, in generative models, such as those trained on existing artworks or music, it is important to ensure that any generated content influenced by these works appropriately credits the original creators. We study credit attribution by machine learning algorithms. We propose new definitions--relaxations of Differential Privacy--that weaken the stability guarantees for a designated subset of $k$ datapoints. These $k$ datapoints can be used non-stably with permission from their owners, potentially in exchange for compensation. Meanwhile, the remaining datapoints are guaranteed to have no significant influence on the algorithm's output. Our framework extends well-studied notions of stability, including Differential Privacy ($k = 0$), differentially private learning with public data (where the $k$ public datapoints are fixed in advance), and stable sample compression (where the $k$ datapoints are selected adaptively by the algorithm). We examine the expressive power of these stability notions within the PAC learning framework, provide a comprehensive characterization of learnability for algorithms adhering to these principles, and propose directions and questions for future research.

Adaptive Data Analysis in a Balanced Adversarial Model

In adaptive data analysis, a mechanism gets $n$ i.i.d. samples from an unknown distribution $D$, and is required to provide accurate estimations to a sequence of adaptively chosen statistical queries with respect to $D$. Hardt and Ullman (FOCS 2014) and Steinke and Ullman (COLT 2015) showed that in general, it is computationally hard to answer more than $\Theta(n^2)$ adaptive queries, assuming the existence of one-way functions. However, these negative results strongly rely on an adversarial model that significantly advantages the adversarial analyst over the mechanism, as the analyst, who chooses the adaptive queries, also chooses the underlying distribution $D$. This imbalance raises questions with respect to the applicability of the obtained hardness results -- an analyst who has complete knowledge of the underlying distribution $D$ would have little need, if at all, to issue statistical queries to a mechanism which only holds a finite number of samples from $D$. We consider more restricted adversaries, called \emph{balanced}, where each such adversary consists of two separated algorithms: The \emph{sampler} who is the entity that chooses the distribution and provides the samples to the mechanism, and the \emph{analyst} who chooses the adaptive queries, but does not have a prior knowledge of the underlying distribution. We improve the quality of previous lower bounds by revisiting them using an efficient \emph{balanced} adversary, under standard public-key cryptography assumptions. We show that these stronger hardness assumptions are unavoidable in the sense that any computationally bounded \emph{balanced} adversary that has the structure of all known attacks, implies the existence of public-key cryptography.

Private Everlasting Prediction

A private learner is trained on a sample of labeled points and generates a hypothesis that can be used for predicting the labels of newly sampled points while protecting the privacy of the training set [Kasiviswannathan et al., FOCS 2008]. Research uncovered that private learners may need to exhibit significantly higher sample complexity than non-private learners as is the case with, e.g., learning of one-dimensional threshold functions [Bun et al., FOCS 2015, Alon et al., STOC 2019]. We explore prediction as an alternative to learning. Instead of putting forward a hypothesis, a predictor answers a stream of classification queries. Earlier work has considered a private prediction model with just a single classification query [Dwork and Feldman, COLT 2018]. We observe that when answering a stream of queries, a predictor must modify the hypothesis it uses over time, and, furthermore, that it must use the queries for this modification, hence introducing potential privacy risks with respect to the queries themselves. We introduce private everlasting prediction taking into account the privacy of both the training set and the (adaptively chosen) queries made to the predictor. We then present a generic construction of private everlasting predictors in the PAC model. The sample complexity of the initial training sample in our construction is quadratic (up to polylog factors) in the VC dimension of the concept class. Our construction allows prediction for all concept classes with finite VC dimension, and in particular threshold functions with constant size initial training sample, even when considered over infinite domains, whereas it is known that the sample complexity of privately learning threshold functions must grow as a function of the domain size and hence is impossible for infinite domains.

On Differentially Private Online Predictions

In this work we introduce an interactive variant of joint differential privacy towards handling online processes in which existing privacy definitions seem too restrictive. We study basic properties of this definition and demonstrate that it satisfies (suitable variants) of group privacy, composition, and post processing. We then study the cost of interactive joint privacy in the basic setting of online classification. We show that any (possibly non-private) learning rule can be effectively transformed to a private learning rule with only a polynomial overhead in the mistake bound. This demonstrates a stark difference with more restrictive notions of privacy such as the one studied by Golowich and Livni (2021), where only a double exponential overhead on the mistake bound is known (via an information theoretic upper bound).

The Sample Complexity of Distribution-Free Parity Learning in the Robust Shuffle Model

We provide a lowerbound on the sample complexity of distribution-free parity learning in the realizable case in the shuffle model of differential privacy. Namely, we show that the sample complexity of learning $d$-bit parity functions is $\Omega(2^{d/2})$. Our result extends a recent similar lowerbound on the sample complexity of private agnostic learning of parity functions in the shuffle model by Cheu and Ullman. We also sketch a simple shuffle model protocol demonstrating that our results are tight up to $poly(d)$ factors.

On the Round Complexity of the Shuffle Model

The shuffle model of differential privacy was proposed as a viable model for performing distributed differentially private computations. Informally, the model consists of an untrusted analyzer that receives messages sent by participating parties via a shuffle functionality, the latter potentially disassociates messages from their senders. Prior work focused on one-round differentially private shuffle model protocols, demonstrating that functionalities such as addition and histograms can be performed in this model with accuracy levels similar to that of the curator model of differential privacy, where the computation is performed by a fully trusted party. Focusing on the round complexity of the shuffle model, we ask in this work what can be computed in the shuffle model of differential privacy with two rounds. Ishai et al. [FOCS 2006] showed how to use one round of the shuffle to establish secret keys between every two parties. Using this primitive to simulate a general secure multi-party protocol increases its round complexity by one. We show how two parties can use one round of the shuffle to send secret messages without having to first establish a secret key, hence retaining round complexity. Combining this primitive with the two-round semi-honest protocol of Applebaun et al. [TCC 2018], we obtain that every randomized functionality can be computed in the shuffle model with an honest majority, in merely two rounds. This includes any differentially private computation. We then move to examine differentially private computations in the shuffle model that (i) do not require the assumption of an honest majority, or (ii) do not admit one-round protocols, even with an honest majority. For that, we introduce two computational tasks: the common-element problem and the nested-common-element problem, for which we show separations between one-round and two-round protocols.

The power of synergy in differential privacy: Combining a small curator with local randomizers

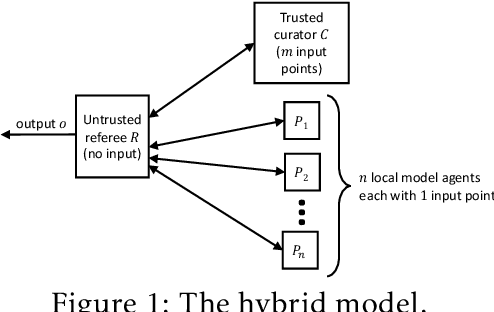
Motivated by the desire to bridge the utility gap between local and trusted curator models of differential privacy for practical applications, we initiate the theoretical study of a hybrid model introduced by "Blender" [Avent et al.,\ USENIX Security '17], in which differentially private protocols of n agents that work in the local-model are assisted by a differentially private curator that has access to the data of m additional users. We focus on the regime where m << n and study the new capabilities of this (m,n)-hybrid model. We show that, despite the fact that the hybrid model adds no significant new capabilities for the basic task of simple hypothesis-testing, there are many other tasks (under a wide range of parameters) that can be solved in the hybrid model yet cannot be solved either by the curator or by the local-users separately. Moreover, we exhibit additional tasks where at least one round of interaction between the curator and the local-users is necessary -- namely, no hybrid model protocol without such interaction can solve these tasks. Taken together, our results show that the combination of the local model with a small curator can become part of a promising toolkit for designing and implementing differential privacy.

Differentially Private Summation with Multi-Message Shuffling

In recent work, Cheu et al. (Eurocrypt 2019) proposed a protocol for $n$-party real summation in the shuffle model of differential privacy with $O_{\epsilon, \delta}(1)$ error and $\Theta(\epsilon\sqrt{n})$ one-bit messages per party. In contrast, every local model protocol for real summation must incur error $\Omega(1/\sqrt{n})$, and there exist protocols matching this lower bound which require just one bit of communication per party. Whether this gap in number of messages is necessary was left open by Cheu et al. In this note we show a protocol with $O(1/\epsilon)$ error and $O(\log(n/\delta))$ messages of size $O(\log(n))$ per party. This protocol is based on the work of Ishai et al.\ (FOCS 2006) showing how to implement distributed summation from secure shuffling, and the observation that this allows simulating the Laplace mechanism in the shuffle model.

The Privacy Blanket of the Shuffle Model

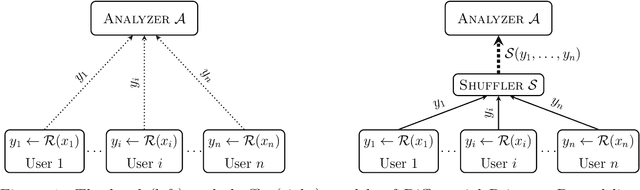
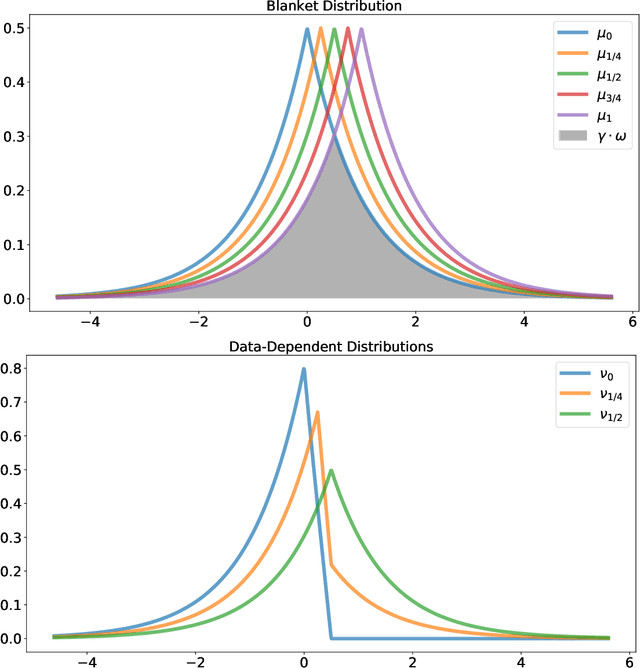
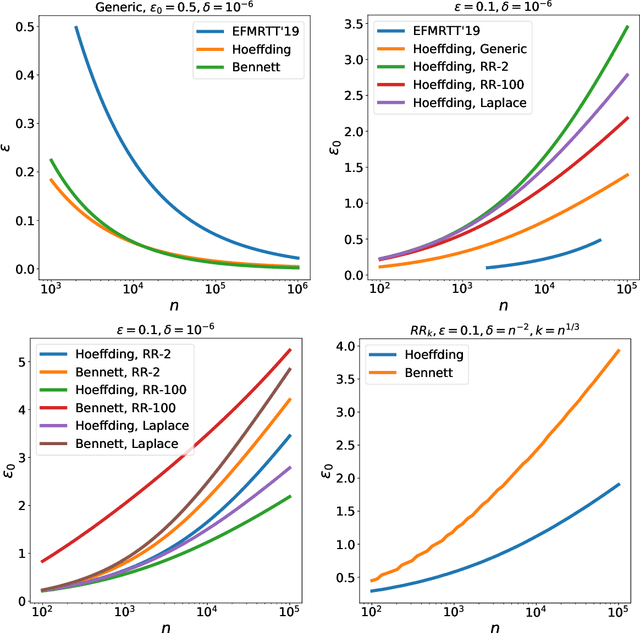
This work studies differential privacy in the context of the recently proposed shuffle model. Unlike in the local model, where the server collecting privatized data from users can track back an input to a specific user, in the shuffle model users submit their privatized inputs to a server anonymously. This setup yields a trust model which sits in between the classical curator and local models for differential privacy. The shuffle model is the core idea in the Encode, Shuffle, Analyze (ESA) model introduced by Bittau et al. (SOPS 2017). Recent work by Cheu et al. (Forthcoming, EUROCRYPT 2019) analyzes the differential privacy properties of the shuffle model and shows that in some cases shuffled protocols provide strictly better accuracy than local protocols. Additionally, Erlignsson et al. (SODA 2019) provide a privacy amplification bound quantifying the level of curator differential privacy achieved by the shuffle model in terms of the local differential privacy of the randomizer used by each user. In this context, we make three contributions. First, we provide an optimal single message protocol for summation of real numbers in the shuffle model. Our protocol is very simple and has better accuracy and communication than the protocols for this same problem proposed by Cheu et al. Optimality of this protocol follows from our second contribution, a new lower bound for the accuracy of private protocols for summation of real numbers in the shuffle model. The third contribution is a new amplification bound for analyzing the privacy of protocols in the shuffle model in terms of the privacy provided by the corresponding local randomizer. Our amplification bound generalizes the results by Erlingsson et al. to a wider range of parameters, and provides a whole family of methods to analyze privacy amplification in the shuffle model.

Private Center Points and Learning of Halfspaces

We present a private learner for halfspaces over an arbitrary finite domain $X\subset \mathbb{R}^d$ with sample complexity $mathrm{poly}(d,2^{\log^*|X|})$. The building block for this learner is a differentially private algorithm for locating an approximate center point of $m>\mathrm{poly}(d,2^{\log^*|X|})$ points -- a high dimensional generalization of the median function. Our construction establishes a relationship between these two problems that is reminiscent of the relation between the median and learning one-dimensional thresholds [Bun et al.\ FOCS '15]. This relationship suggests that the problem of privately locating a center point may have further applications in the design of differentially private algorithms. We also provide a lower bound on the sample complexity for privately finding a point in the convex hull. For approximate differential privacy, we show a lower bound of $m=\Omega(d+\log^*|X|)$, whereas for pure differential privacy $m=\Omega(d\log|X|)$.