Relaxed Models for Adversarial Streaming: The Advice Model and the Bounded Interruptions Model

Streaming algorithms are typically analyzed in the oblivious setting, where we assume that the input stream is fixed in advance. Recently, there is a growing interest in designing adversarially robust streaming algorithms that must maintain utility even when the input stream is chosen adaptively and adversarially as the execution progresses. While several fascinating results are known for the adversarial setting, in general, it comes at a very high cost in terms of the required space. Motivated by this, in this work we set out to explore intermediate models that allow us to interpolate between the oblivious and the adversarial models. Specifically, we put forward the following two models: (1) *The advice model*, in which the streaming algorithm may occasionally ask for one bit of advice. (2) *The bounded interruptions model*, in which we assume that the adversary is only partially adaptive. We present both positive and negative results for each of these two models. In particular, we present generic reductions from each of these models to the oblivious model. This allows us to design robust algorithms with significantly improved space complexity compared to what is known in the plain adversarial model.

Differentially-Private Bayes Consistency

We construct a universally Bayes consistent learning rule that satisfies differential privacy (DP). We first handle the setting of binary classification and then extend our rule to the more general setting of density estimation (with respect to the total variation metric). The existence of a universally consistent DP learner reveals a stark difference with the distribution-free PAC model. Indeed, in the latter DP learning is extremely limited: even one-dimensional linear classifiers are not privately learnable in this stringent model. Our result thus demonstrates that by allowing the learning rate to depend on the target distribution, one can circumvent the above-mentioned impossibility result and in fact, learn \emph{arbitrary} distributions by a single DP algorithm. As an application, we prove that any VC class can be privately learned in a semi-supervised setting with a near-optimal \emph{labeled} sample complexity of $\tilde{O}(d/\varepsilon)$ labeled examples (and with an unlabeled sample complexity that can depend on the target distribution).

Adaptive Data Analysis with Correlated Observations

The vast majority of the work on adaptive data analysis focuses on the case where the samples in the dataset are independent. Several approaches and tools have been successfully applied in this context, such as differential privacy, max-information, compression arguments, and more. The situation is far less well-understood without the independence assumption. We embark on a systematic study of the possibilities of adaptive data analysis with correlated observations. First, we show that, in some cases, differential privacy guarantees generalization even when there are dependencies within the sample, which we quantify using a notion we call Gibbs-dependence. We complement this result with a tight negative example. Second, we show that the connection between transcript-compression and adaptive data analysis can be extended to the non-iid setting.

On the Sample Complexity of Privately Learning Axis-Aligned Rectangles

We revisit the fundamental problem of learning Axis-Aligned-Rectangles over a finite grid $X^d\subseteq{\mathbb{R}}^d$ with differential privacy. Existing results show that the sample complexity of this problem is at most $\min\left\{ d{\cdot}\log|X| \;,\; d^{1.5}{\cdot}\left(\log^*|X| \right)^{1.5}\right\}$. That is, existing constructions either require sample complexity that grows linearly with $\log|X|$, or else it grows super linearly with the dimension $d$. We present a novel algorithm that reduces the sample complexity to only $\tilde{O}\left\{d{\cdot}\left(\log^*|X|\right)^{1.5}\right\}$, attaining a dimensionality optimal dependency without requiring the sample complexity to grow with $\log|X|$.The technique used in order to attain this improvement involves the deletion of "exposed" data-points on the go, in a fashion designed to avoid the cost of the adaptive composition theorems. The core of this technique may be of individual interest, introducing a new method for constructing statistically-efficient private algorithms.

Agnostic Sample Compression for Linear Regression

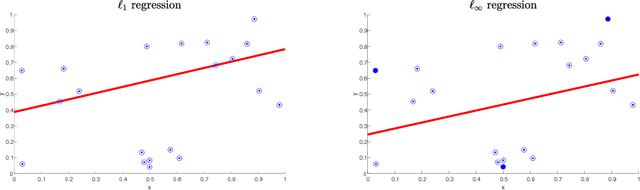
We obtain the first positive results for bounded sample compression in the agnostic regression setting. We show that for p in {1,infinity}, agnostic linear regression with $\ell_p$ loss admits a bounded sample compression scheme. Specifically, we exhibit efficient sample compression schemes for agnostic linear regression in $R^d$ of size $d+1$ under the $\ell_1$ loss and size $d+2$ under the $\ell_\infty$ loss. We further show that for every other $\ell_p$ loss (1 < p < infinity), there does not exist an agnostic compression scheme of bounded size. This refines and generalizes a negative result of David, Moran, and Yehudayoff (2016) for the $\ell_2$ loss. We close by posing a general open question: for agnostic regression with $\ell_1$ loss, does every function class admit a compression scheme of size equal to its pseudo-dimension? This question generalizes Warmuth's classic sample compression conjecture for realizable-case classification (Warmuth, 2003).

Sample Compression for Real-Valued Learners

We give an algorithmically efficient version of the learner-to-compression scheme conversion in Moran and Yehudayoff (2016). In extending this technique to real-valued hypotheses, we also obtain an efficient regression-to-bounded sample compression converter. To our knowledge, this is the first general compressed regression result (regardless of efficiency or boundedness) guaranteeing uniform approximate reconstruction. Along the way, we develop a generic procedure for constructing weak real-valued learners out of abstract regressors; this may be of independent interest. In particular, this result sheds new light on an open question of H. Simon (1997). We show applications to two regression problems: learning Lipschitz and bounded-variation functions.