On Differentially Private Subspace Estimation Without Distributional Assumptions

Private data analysis faces a significant challenge known as the curse of dimensionality, leading to increased costs. However, many datasets possess an inherent low-dimensional structure. For instance, during optimization via gradient descent, the gradients frequently reside near a low-dimensional subspace. If the low-dimensional structure could be privately identified using a small amount of points, we could avoid paying (in terms of privacy and accuracy) for the high ambient dimension. On the negative side, Dwork, Talwar, Thakurta, and Zhang (STOC 2014) proved that privately estimating subspaces, in general, requires an amount of points that depends on the dimension. But Singhal and Steinke (NeurIPS 2021) bypassed this limitation by considering points that are i.i.d. samples from a Gaussian distribution whose covariance matrix has a certain eigenvalue gap. Yet, it was still left unclear whether we could provide similar upper bounds without distributional assumptions and whether we could prove lower bounds that depend on similar eigenvalue gaps. In this work, we make progress in both directions. We formulate the problem of private subspace estimation under two different types of singular value gaps of the input data and prove new upper and lower bounds for both types. In particular, our results determine what type of gap is sufficient and necessary for estimating a subspace with an amount of points that is independent of the dimension.

Smooth Lower Bounds for Differentially Private Algorithms via Padding-and-Permuting Fingerprinting Codes

Fingerprinting arguments, first introduced by Bun, Ullman, and Vadhan (STOC 2014), are the most widely used method for establishing lower bounds on the sample complexity or error of approximately differentially private (DP) algorithms. Still, there are many problems in differential privacy for which we don't know suitable lower bounds, and even for problems that we do, the lower bounds are not smooth, and usually become vacuous when the error is larger than some threshold. In this work, we present a simple method to generate hard instances by applying a padding-and-permuting transformation to a fingerprinting code. We illustrate the applicability of this method by providing new lower bounds in various settings: 1. A tight lower bound for DP averaging in the low-accuracy regime, which in particular implies a new lower bound for the private 1-cluster problem introduced by Nissim, Stemmer, and Vadhan (PODS 2016). 2. A lower bound on the additive error of DP algorithms for approximate k-means clustering, as a function of the multiplicative error, which is tight for a constant multiplication error. 3. A lower bound for estimating the top singular vector of a matrix under DP in low-accuracy regimes, which is a special case of DP subspace estimation studied by Singhal and Steinke (NeurIPS 2021). Our main technique is to apply a padding-and-permuting transformation to a fingerprinting code. However, rather than proving our results using a black-box access to an existing fingerprinting code (e.g., Tardos' code), we develop a new fingerprinting lemma that is stronger than those of Dwork et al. (FOCS 2015) and Bun et al. (SODA 2017), and prove our lower bounds directly from the lemma. Our lemma, in particular, gives a simpler fingerprinting code construction with optimal rate (up to polylogarithmic factors) that is of independent interest.

Adaptive Data Analysis in a Balanced Adversarial Model

In adaptive data analysis, a mechanism gets $n$ i.i.d. samples from an unknown distribution $D$, and is required to provide accurate estimations to a sequence of adaptively chosen statistical queries with respect to $D$. Hardt and Ullman (FOCS 2014) and Steinke and Ullman (COLT 2015) showed that in general, it is computationally hard to answer more than $\Theta(n^2)$ adaptive queries, assuming the existence of one-way functions. However, these negative results strongly rely on an adversarial model that significantly advantages the adversarial analyst over the mechanism, as the analyst, who chooses the adaptive queries, also chooses the underlying distribution $D$. This imbalance raises questions with respect to the applicability of the obtained hardness results -- an analyst who has complete knowledge of the underlying distribution $D$ would have little need, if at all, to issue statistical queries to a mechanism which only holds a finite number of samples from $D$. We consider more restricted adversaries, called \emph{balanced}, where each such adversary consists of two separated algorithms: The \emph{sampler} who is the entity that chooses the distribution and provides the samples to the mechanism, and the \emph{analyst} who chooses the adaptive queries, but does not have a prior knowledge of the underlying distribution. We improve the quality of previous lower bounds by revisiting them using an efficient \emph{balanced} adversary, under standard public-key cryptography assumptions. We show that these stronger hardness assumptions are unavoidable in the sense that any computationally bounded \emph{balanced} adversary that has the structure of all known attacks, implies the existence of public-key cryptography.

Differentially-Private Clustering of Easy Instances

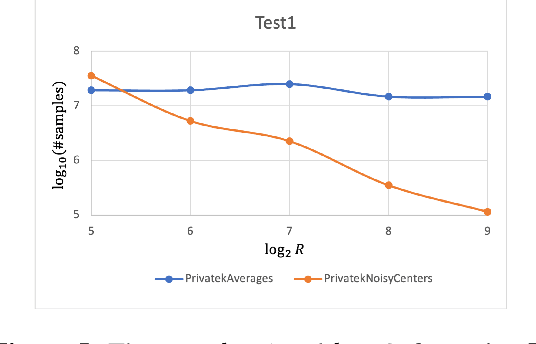
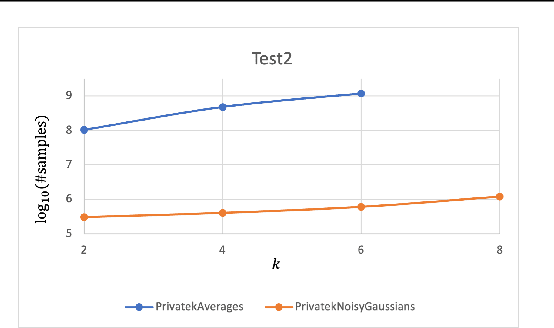
Clustering is a fundamental problem in data analysis. In differentially private clustering, the goal is to identify $k$ cluster centers without disclosing information on individual data points. Despite significant research progress, the problem had so far resisted practical solutions. In this work we aim at providing simple implementable differentially private clustering algorithms that provide utility when the data is "easy," e.g., when there exists a significant separation between the clusters. We propose a framework that allows us to apply non-private clustering algorithms to the easy instances and privately combine the results. We are able to get improved sample complexity bounds in some cases of Gaussian mixtures and $k$-means. We complement our theoretical analysis with an empirical evaluation on synthetic data.

FriendlyCore: Practical Differentially Private Aggregation

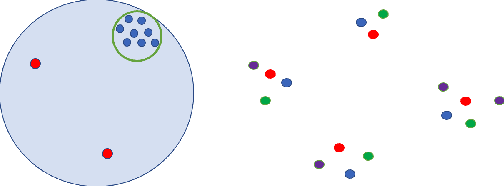
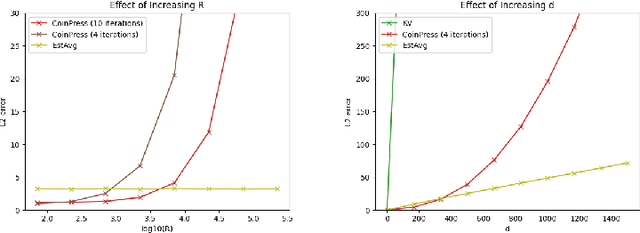
Differentially private algorithms for common metric aggregation tasks, such as clustering or averaging, often have limited practicality due to their complexity or a large number of data points that is required for accurate results. We propose a simple and practical tool $\mathsf{FriendlyCore}$ that takes a set of points ${\cal D}$ from an unrestricted (pseudo) metric space as input. When ${\cal D}$ has effective diameter $r$, $\mathsf{FriendlyCore}$ returns a "stable" subset ${\cal D}_G\subseteq {\cal D}$ that includes all points, except possibly few outliers, and is {\em certified} to have diameter $r$. $\mathsf{FriendlyCore}$ can be used to preprocess the input before privately aggregating it, potentially simplifying the aggregation or boosting its accuracy. Surprisingly, $\mathsf{FriendlyCore}$ is light-weight with no dependence on the dimension. We empirically demonstrate its advantages in boosting the accuracy of mean estimation, outperforming tailored methods.

Private Learning of Halfspaces: Simplifying the Construction and Reducing the Sample Complexity

We present a differentially private learner for halfspaces over a finite grid $G$ in $\mathbb{R}^d$ with sample complexity $\approx d^{2.5}\cdot 2^{\log^*|G|}$, which improves the state-of-the-art result of [Beimel et al., COLT 2019] by a $d^2$ factor. The building block for our learner is a new differentially private algorithm for approximately solving the linear feasibility problem: Given a feasible collection of $m$ linear constraints of the form $Ax\geq b$, the task is to privately identify a solution $x$ that satisfies most of the constraints. Our algorithm is iterative, where each iteration determines the next coordinate of the constructed solution $x$.