Concurrent Shuffle Differential Privacy Under Continual Observation

We introduce the concurrent shuffle model of differential privacy. In this model we have multiple concurrent shufflers permuting messages from different, possibly overlapping, batches of users. Similarly to the standard (single) shuffle model, the privacy requirement is that the concatenation of all shuffled messages should be differentially private. We study the private continual summation problem (a.k.a. the counter problem) and show that the concurrent shuffle model allows for significantly improved error compared to a standard (single) shuffle model. Specifically, we give a summation algorithm with error $\tilde{O}(n^{1/(2k+1)})$ with $k$ concurrent shufflers on a sequence of length $n$. Furthermore, we prove that this bound is tight for any $k$, even if the algorithm can choose the sizes of the batches adaptively. For $k=\log n$ shufflers, the resulting error is polylogarithmic, much better than $\tilde{\Theta}(n^{1/3})$ which we show is the smallest possible with a single shuffler. We use our online summation algorithm to get algorithms with improved regret bounds for the contextual linear bandit problem. In particular we get optimal $\tilde{O}(\sqrt{n})$ regret with $k= \tilde{\Omega}(\log n)$ concurrent shufflers.

Prompt-to-Prompt Image Editing with Cross Attention Control

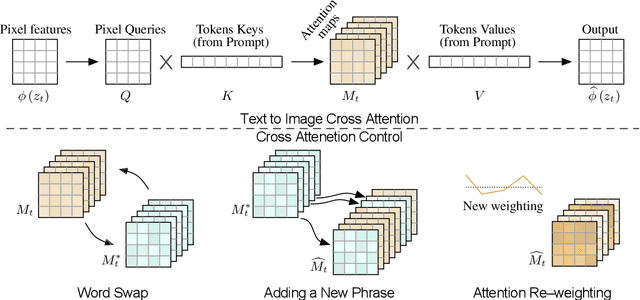
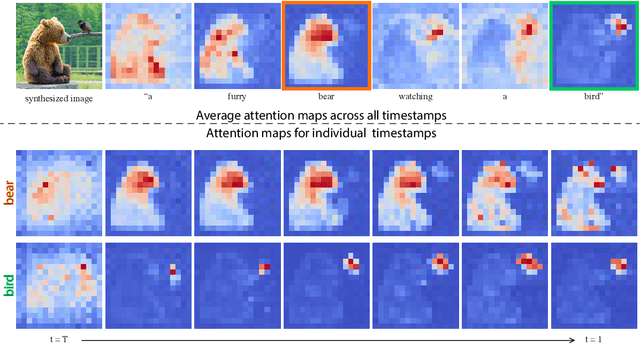
Recent large-scale text-driven synthesis models have attracted much attention thanks to their remarkable capabilities of generating highly diverse images that follow given text prompts. Such text-based synthesis methods are particularly appealing to humans who are used to verbally describe their intent. Therefore, it is only natural to extend the text-driven image synthesis to text-driven image editing. Editing is challenging for these generative models, since an innate property of an editing technique is to preserve most of the original image, while in the text-based models, even a small modification of the text prompt often leads to a completely different outcome. State-of-the-art methods mitigate this by requiring the users to provide a spatial mask to localize the edit, hence, ignoring the original structure and content within the masked region. In this paper, we pursue an intuitive prompt-to-prompt editing framework, where the edits are controlled by text only. To this end, we analyze a text-conditioned model in depth and observe that the cross-attention layers are the key to controlling the relation between the spatial layout of the image to each word in the prompt. With this observation, we present several applications which monitor the image synthesis by editing the textual prompt only. This includes localized editing by replacing a word, global editing by adding a specification, and even delicately controlling the extent to which a word is reflected in the image. We present our results over diverse images and prompts, demonstrating high-quality synthesis and fidelity to the edited prompts.

Differentially Private Multi-Armed Bandits in the Shuffle Model

We give an $(\varepsilon,\delta)$-differentially private algorithm for the multi-armed bandit (MAB) problem in the shuffle model with a distribution-dependent regret of $O\left(\left(\sum_{a\in [k]:\Delta_a>0}\frac{\log T}{\Delta_a}\right)+\frac{k\sqrt{\log\frac{1}{\delta}}\log T}{\varepsilon}\right)$, and a distribution-independent regret of $O\left(\sqrt{kT\log T}+\frac{k\sqrt{\log\frac{1}{\delta}}\log T}{\varepsilon}\right)$, where $T$ is the number of rounds, $\Delta_a$ is the suboptimality gap of the arm $a$, and $k$ is the total number of arms. Our upper bound almost matches the regret of the best known algorithms for the centralized model, and significantly outperforms the best known algorithm in the local model.

Locality Sensitive Hashing for Efficient Similar Polygon Retrieval

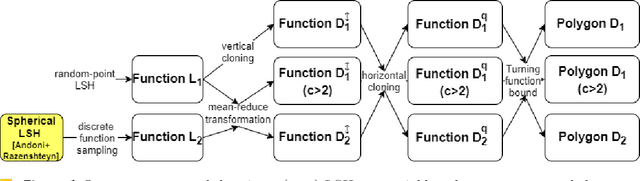
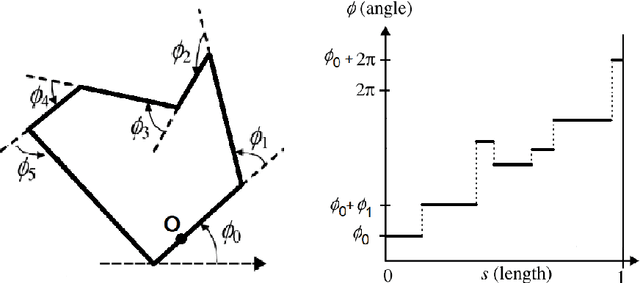
Locality Sensitive Hashing (LSH) is an effective method of indexing a set of items to support efficient nearest neighbors queries in high-dimensional spaces. The basic idea of LSH is that similar items should produce hash collisions with higher probability than dissimilar items. We study LSH for (not necessarily convex) polygons, and use it to give efficient data structures for similar shape retrieval. Arkin et al. represent polygons by their "turning function" - a function which follows the angle between the polygon's tangent and the $ x $-axis while traversing the perimeter of the polygon. They define the distance between polygons to be variations of the $ L_p $ (for $p=1,2$) distance between their turning functions. This metric is invariant under translation, rotation and scaling (and the selection of the initial point on the perimeter) and therefore models well the intuitive notion of shape resemblance. We develop and analyze LSH near neighbor data structures for several variations of the $ L_p $ distance for functions (for $p=1,2$). By applying our schemes to the turning functions of a collection of polygons we obtain efficient near neighbor LSH-based structures for polygons. To tune our structures to turning functions of polygons, we prove some new properties of these turning functions that may be of independent interest. As part of our analysis, we address the following problem which is of independent interest. Find the vertical translation of a function $ f $ that is closest in $ L_1 $ distance to a function $ g $. We prove tight bounds on the approximation guarantee obtained by the translation which is equal to the difference between the averages of $ g $ and $ f $.