Structure-constrained Language-informed Diffusion Model for Unpaired Low-dose Computed Tomography Angiography Reconstruction

The application of iodinated contrast media (ICM) improves the sensitivity and specificity of computed tomography (CT) for a wide range of clinical indications. However, overdose of ICM can cause problems such as kidney damage and life-threatening allergic reactions. Deep learning methods can generate CT images of normal-dose ICM from low-dose ICM, reducing the required dose while maintaining diagnostic power. However, existing methods are difficult to realize accurate enhancement with incompletely paired images, mainly because of the limited ability of the model to recognize specific structures. To overcome this limitation, we propose a Structure-constrained Language-informed Diffusion Model (SLDM), a unified medical generation model that integrates structural synergy and spatial intelligence. First, the structural prior information of the image is effectively extracted to constrain the model inference process, thus ensuring structural consistency in the enhancement process. Subsequently, semantic supervision strategy with spatial intelligence is introduced, which integrates the functions of visual perception and spatial reasoning, thus prompting the model to achieve accurate enhancement. Finally, the subtraction angiography enhancement module is applied, which serves to improve the contrast of the ICM agent region to suitable interval for observation. Qualitative analysis of visual comparison and quantitative results of several metrics demonstrate the effectiveness of our method in angiographic reconstruction for low-dose contrast medium CT angiography.

On the Influence of Smoothness Constraints in Computed Tomography Motion Compensation

Computed tomography (CT) relies on precise patient immobilization during image acquisition. Nevertheless, motion artifacts in the reconstructed images can persist. Motion compensation methods aim to correct such artifacts post-acquisition, often incorporating temporal smoothness constraints on the estimated motion patterns. This study analyzes the influence of a spline-based motion model within an existing rigid motion compensation algorithm for cone-beam CT on the recoverable motion frequencies. Results demonstrate that the choice of motion model crucially influences recoverable frequencies. The optimization-based motion compensation algorithm is able to accurately fit the spline nodes for frequencies almost up to the node-dependent theoretical limit according to the Nyquist-Shannon theorem. Notably, a higher node count does not compromise reconstruction performance for slow motion patterns, but can extend the range of recoverable high frequencies for the investigated algorithm. Eventually, the optimal motion model is dependent on the imaged anatomy, clinical use case, and scanning protocol and should be tailored carefully to the expected motion frequency spectrum to ensure accurate motion compensation.

A gradient-based approach to fast and accurate head motion compensation in cone-beam CT

Cone-beam computed tomography (CBCT) systems, with their portability, present a promising avenue for direct point-of-care medical imaging, particularly in critical scenarios such as acute stroke assessment. However, the integration of CBCT into clinical workflows faces challenges, primarily linked to long scan duration resulting in patient motion during scanning and leading to image quality degradation in the reconstructed volumes. This paper introduces a novel approach to CBCT motion estimation using a gradient-based optimization algorithm, which leverages generalized derivatives of the backprojection operator for cone-beam CT geometries. Building on that, a fully differentiable target function is formulated which grades the quality of the current motion estimate in reconstruction space. We drastically accelerate motion estimation yielding a 19-fold speed-up compared to existing methods. Additionally, we investigate the architecture of networks used for quality metric regression and propose predicting voxel-wise quality maps, favoring autoencoder-like architectures over contracting ones. This modification improves gradient flow, leading to more accurate motion estimation. The presented method is evaluated through realistic experiments on head anatomy. It achieves a reduction in reprojection error from an initial average of 3mm to 0.61mm after motion compensation and consistently demonstrates superior performance compared to existing approaches. The analytic Jacobian for the backprojection operation, which is at the core of the proposed method, is made publicly available. In summary, this paper contributes to the advancement of CBCT integration into clinical workflows by proposing a robust motion estimation approach that enhances efficiency and accuracy, addressing critical challenges in time-sensitive scenarios.

OSNet & MNetO: Two Types of General Reconstruction Architectures for Linear Computed Tomography in Multi-Scenarios

Recently, linear computed tomography (LCT) systems have actively attracted attention. To weaken projection truncation and image the region of interest (ROI) for LCT, the backprojection filtration (BPF) algorithm is an effective solution. However, in BPF for LCT, it is difficult to achieve stable interior reconstruction, and for differentiated backprojection (DBP) images of LCT, multiple rotation-finite inversion of Hilbert transform (Hilbert filtering)-inverse rotation operations will blur the image. To satisfy multiple reconstruction scenarios for LCT, including interior ROI, complete object, and exterior region beyond field-of-view (FOV), and avoid the rotation operations of Hilbert filtering, we propose two types of reconstruction architectures. The first overlays multiple DBP images to obtain a complete DBP image, then uses a network to learn the overlying Hilbert filtering function, referred to as the Overlay-Single Network (OSNet). The second uses multiple networks to train different directional Hilbert filtering models for DBP images of multiple linear scannings, respectively, and then overlays the reconstructed results, i.e., Multiple Networks Overlaying (MNetO). In two architectures, we introduce a Swin Transformer (ST) block to the generator of pix2pixGAN to extract both local and global features from DBP images at the same time. We investigate two architectures from different networks, FOV sizes, pixel sizes, number of projections, geometric magnification, and processing time. Experimental results show that two architectures can both recover images. OSNet outperforms BPF in various scenarios. For the different networks, ST-pix2pixGAN is superior to pix2pixGAN and CycleGAN. MNetO exhibits a few artifacts due to the differences among the multiple models, but any one of its models is suitable for imaging the exterior edge in a certain direction.

Constructing Custom Thermodynamics Using Deep Learning

One of the most exciting applications of AI is automated scientific discovery based on previously amassed data, coupled with restrictions provided by the known physical principles, including symmetries and conservation laws. Such automated hypothesis creation and verification can assist scientists in studying complex phenomena, where traditional physical intuition may fail. Of particular importance are complex dynamic systems where their time evolution is strongly influenced by varying external parameters. In this paper we develop a platform based on a generalised Onsager principle to learn macroscopic dynamical descriptions of arbitrary stochastic dissipative systems directly from observations of their microscopic trajectories. We focus on systems whose complexity and sheer sizes render complete microscopic description impractical, and constructing theoretical macroscopic models requires extensive domain knowledge or trial-and-error. Our machine learning approach addresses this by simultaneously constructing reduced thermodynamic coordinates and interpreting the dynamics on these coordinates. We demonstrate our method by studying theoretically and validating experimentally, the stretching of long polymer chains in an externally applied field. Specifically, we learn three interpretable thermodynamic coordinates and build a dynamical landscape of polymer stretching, including (1) the identification of stable and transition states and (2) the control of the stretching rate. We further demonstrate the universality of our approach by applying it to an unrelated problem in a different domain: constructing macroscopic dynamics for spatial epidemics, showing that our method addresses wide scientific and technological applications.

BPF Algorithms for Multiple Source-Translation Computed Tomography Reconstruction

Micro-computed tomography (micro-CT) is a widely used state-of-the-art instrument employed to study the morphological structures of objects in various fields. Object-rotation is a classical scanning mode in micro-CT allowing data acquisition from different angles; however, its field-of-view (FOV) is primarily constrained by the size of the detector when aiming for high spatial resolution imaging. Recently, we introduced a novel scanning mode called multiple source translation CT (mSTCT), which effectively enlarges the FOV of the micro-CT system. Furthermore, we developed a virtual projection-based filtered backprojection (V-FBP) algorithm to address truncated projection, albeit with a trade-off in acquisition efficiency (high resolution reconstruction typically requires thousands of source samplings). In this paper, we present a new algorithm for mSTCT reconstruction, backprojection-filtration (BPF), which enables reconstructions of high-resolution images with a low source sampling ratio. Additionally, we found that implementing derivatives in BPF along different directions (source and detector) yields two distinct BPF algorithms (S-BPF and D-BPF), each with its own reconstruction performance characteristics. Through simulated and real experiments conducted in this paper, we demonstrate that achieving same high-resolution reconstructions, D-BPF can reduce source sampling by 75% compared with V-FBP. S-BPF shares similar characteristics with V-FBP, where the spatial resolution is primarily influenced by the source sampling.

OnsagerNet: Learning Stable and Interpretable Dynamics using a Generalized Onsager Principle

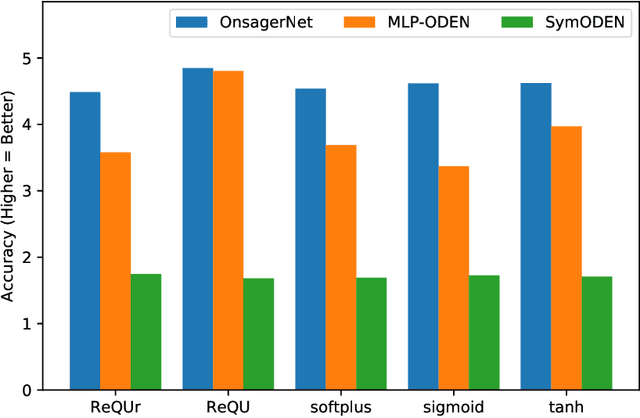
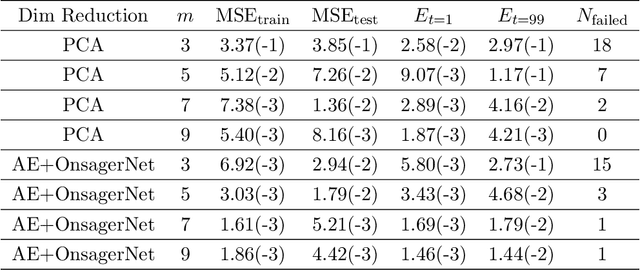
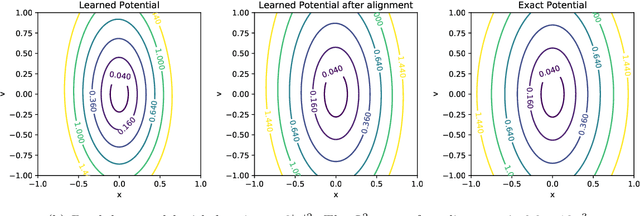
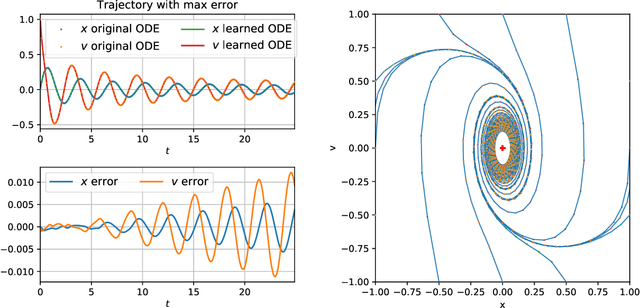
We propose a systematic method for learning stable and interpretable dynamical models using sampled trajectory data from physical processes based on a generalized Onsager principle. The learned dynamics are autonomous ordinary differential equations parameterized by neural networks that retain clear physical structure information, such as free energy, dissipation, conservative interaction and external force. The neural network representations for the hidden dynamics are trained by minimizing the empirical risk based on an embedded Runge-Kutta method. For high dimensional problems with a low dimensional slow manifold, an autoencoder with isometric regularization is introduced to find generalized coordinates on which we learn the Onsager dynamics. We apply the method to learn reduced order models for the Rayleigh-B\'{e}nard convection problem, where we obtain low dimensional autonomous equations that capture both qualitative and quantitative properties of the underlying dynamics. In particular, this validates the basic approach of Lorenz, although we also discover that the dimension of the learned autonomous model required for faithful representation increases with the Rayleigh number.

ChebNet: Efficient and Stable Constructions of Deep Neural Networks with Rectified Power Units using Chebyshev Approximations

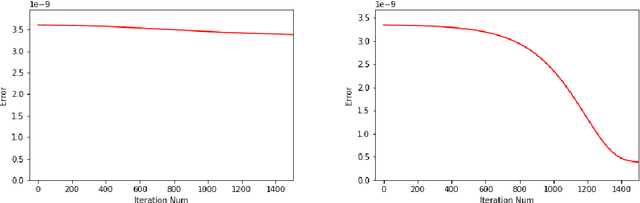
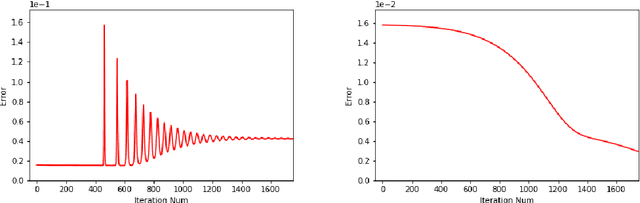
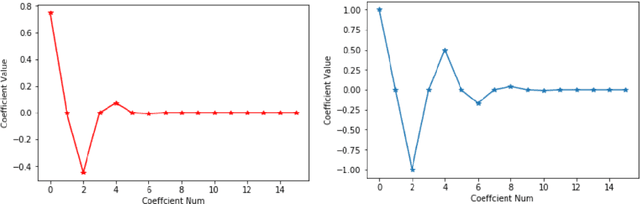
In a recent paper [B. Li, S. Tang and H. Yu, arXiv:1903.05858], it was shown that deep neural networks built with rectified power units (RePU) can give better approximation for sufficient smooth functions than those with rectified linear units, by converting polynomial approximation given in power series into deep neural networks with optimal complexity and no approximation error. However, in practice, power series are not easy to compute. In this paper, we propose a new and more stable way to construct deep RePU neural networks based on Chebyshev polynomial approximations. By using a hierarchical structure of Chebyshev polynomial approximation in frequency domain, we build efficient and stable deep neural network constructions. In theory, ChebNets and the deep RePU nets based on Power series have the same upper error bounds for general function approximations. But numerically, ChebNets are much more stable. Numerical results show that the constructed ChebNets can be further trained and obtain much better results than those obtained by training deep RePU nets constructed basing on power series.

PowerNet: Efficient Representations of Polynomials and Smooth Functions by Deep Neural Networks with Rectified Power Units

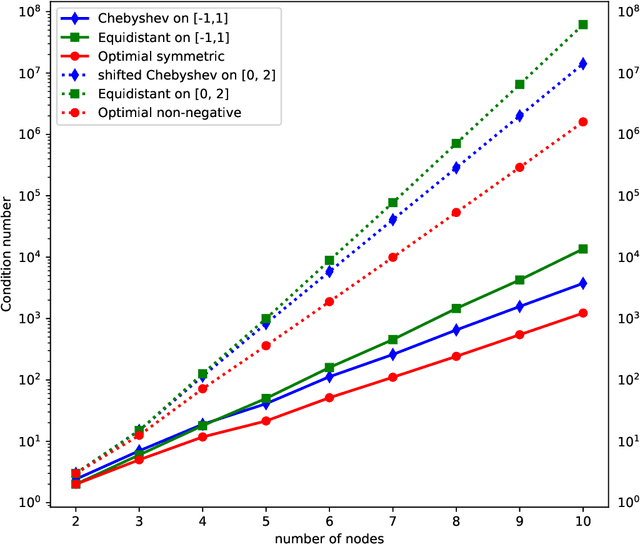
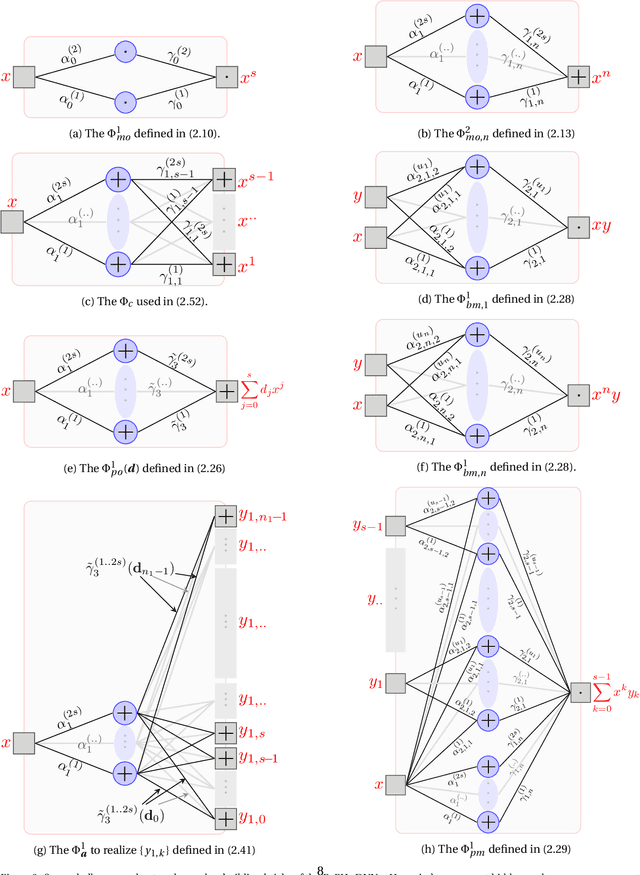
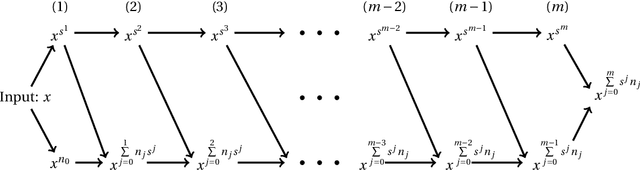
Deep neural network with rectified linear units (ReLU) is getting more and more popular recently. However, the derivatives of the function represented by a ReLU network are not continuous, which limit the usage of ReLU network to situations only when smoothness is not required. In this paper, we construct deep neural networks with rectified power units (RePU), which can give better approximations for smooth functions. Optimal algorithms are proposed to explicitly build neural networks with sparsely connected RePUs, which we call PowerNets, to represent polynomials with no approximation error. For general smooth functions, we first project the function to their polynomial approximations, then use the proposed algorithms to construct corresponding PowerNets. Thus, the error of best polynomial approximation provides an upper bound of the best RePU network approximation error. For smooth functions in higher dimensional Sobolev spaces, we use fast spectral transforms for tensor-product grid and sparse grid discretization to get polynomial approximations. Our constructive algorithms show clearly a close connection between spectral methods and deep neural networks: a PowerNet with $n$ layers can exactly represent polynomials up to degree $s^n$, where $s$ is the power of RePUs. The proposed PowerNets have potential applications in the situations where high-accuracy is desired or smoothness is required.

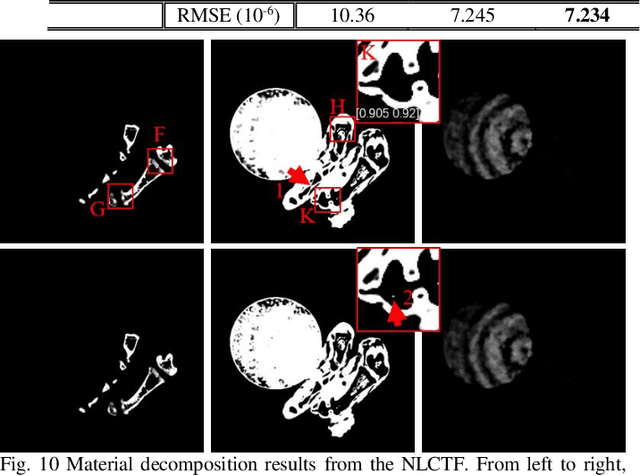
DLIMD: Dictionary Learning based Image-domain Material Decomposition for spectral CT

The potential huge advantage of spectral computed tomography (CT) is its capability to provide accuracy material identification and quantitative tissue information. This can benefit clinical applications, such as brain angiography, early tumor recognition, etc. To achieve more accurate material components with higher material image quality, we develop a dictionary learning based image-domain material decomposition (DLIMD) for spectral CT in this paper. First, we reconstruct spectral CT image from projections and calculate material coefficients matrix by selecting uniform regions of basis materials from image reconstruction results. Second, we employ the direct inversion (DI) method to obtain initial material decomposition results, and a set of image patches are extracted from the mode-1 unfolding of normalized material image tensor to train a united dictionary by the K-SVD technique. Third, the trained dictionary is employed to explore the similarities from decomposed material images by constructing the DLIMD model. Fourth, more constraints (i.e., volume conservation and the bounds of each pixel within material maps) are further integrated into the model to improve the accuracy of material decomposition. Finally, both physical phantom and preclinical experiments are employed to evaluate the performance of the proposed DLIMD in material decomposition accuracy, material image edge preservation and feature recovery.