Backdiff: a diffusion model for generalized transferable protein backmapping

Coarse-grained (CG) models play a crucial role in the study of protein structures, protein thermodynamic properties, and protein conformation dynamics. Due to the information loss in the coarse-graining process, backmapping from CG to all-atom configurations is essential in many protein design and drug discovery applications when detailed atomic representations are needed for in-depth studies. Despite recent progress in data-driven backmapping approaches, devising a backmapping method that can be universally applied across various CG models and proteins remains unresolved. In this work, we propose BackDiff, a new generative model designed to achieve generalization and reliability in the protein backmapping problem. BackDiff leverages the conditional score-based diffusion model with geometric representations. Since different CG models can contain different coarse-grained sites which include selected atoms (CG atoms) and simple CG auxiliary functions of atomistic coordinates (CG auxiliary variables), we design a self-supervised training framework to adapt to different CG atoms, and constrain the diffusion sampling paths with arbitrary CG auxiliary variables as conditions. Our method facilitates end-to-end training and allows efficient sampling across different proteins and diverse CG models without the need for retraining. Comprehensive experiments over multiple popular CG models demonstrate BackDiff's superior performance to existing state-of-the-art approaches, and generalization and flexibility that these approaches cannot achieve. A pretrained BackDiff model can offer a convenient yet reliable plug-and-play solution for protein researchers, enabling them to investigate further from their own CG models.

An Element-wise RSAV Algorithm for Unconstrained Optimization Problems

We present a novel optimization algorithm, element-wise relaxed scalar auxiliary variable (E-RSAV), that satisfies an unconditional energy dissipation law and exhibits improved alignment between the modified and the original energy. Our algorithm features rigorous proofs of linear convergence in the convex setting. Furthermore, we present a simple accelerated algorithm that improves the linear convergence rate to super-linear in the univariate case. We also propose an adaptive version of E-RSAV with Steffensen step size. We validate the robustness and fast convergence of our algorithm through ample numerical experiments.

Multi-Subdomain Adversarial Network for Cross-Subject EEG-based Emotion Recognition

The individual difference between subjects is significant in EEG-based emotion recognition, resulting in the difficulty of sharing the model across subjects. Previous studies use domain adaptation algorithms to minimize the global domain discrepancy while ignoring the class information, which may cause misalignment of subdomains and reduce model performance. This paper proposes a multi-subdomain adversarial network (MSAN) for cross-subject EEG-based emotion recognition. MSAN uses adversarial training to model the discrepancy in the global domain and subdomain to reduce the intra-class distance and enlarge the inter-class distance. In addition, MSAN initializes parameters through a pre-trained autoencoder to ensure the stability and convertibility of the model. The experimental results show that the accuracy of MSAN is improved by 30.02\% on the SEED dataset comparing with the nontransfer method.

Energy-Dissipative Evolutionary Deep Operator Neural Networks

Energy-Dissipative Evolutionary Deep Operator Neural Network is an operator learning neural network. It is designed to seed numerical solutions for a class of partial differential equations instead of a single partial differential equation, such as partial differential equations with different parameters or different initial conditions. The network consists of two sub-networks, the Branch net and the Trunk net. For an objective operator G, the Branch net encodes different input functions u at the same number of sensors, and the Trunk net evaluates the output function at any location. By minimizing the error between the evaluated output q and the expected output G(u)(y), DeepONet generates a good approximation of the operator G. In order to preserve essential physical properties of PDEs, such as the Energy Dissipation Law, we adopt a scalar auxiliary variable approach to generate the minimization problem. It introduces a modified energy and enables unconditional energy dissipation law at the discrete level. By taking the parameter as a function of time t, this network can predict the accurate solution at any further time with feeding data only at the initial state. The data needed can be generated by the initial conditions, which are readily available. In order to validate the accuracy and efficiency of our neural networks, we provide numerical simulations of several partial differential equations, including heat equations, parametric heat equations and Allen-Cahn equations.

HomPINNs: homotopy physics-informed neural networks for solving the inverse problems of nonlinear differential equations with multiple solutions

Due to the complex behavior arising from non-uniqueness, symmetry, and bifurcations in the solution space, solving inverse problems of nonlinear differential equations (DEs) with multiple solutions is a challenging task. To address this issue, we propose homotopy physics-informed neural networks (HomPINNs), a novel framework that leverages homotopy continuation and neural networks (NNs) to solve inverse problems. The proposed framework begins with the use of a NN to simultaneously approximate known observations and conform to the constraints of DEs. By utilizing the homotopy continuation method, the approximation traces the observations to identify multiple solutions and solve the inverse problem. The experiments involve testing the performance of the proposed method on one-dimensional DEs and applying it to solve a two-dimensional Gray-Scott simulation. Our findings demonstrate that the proposed method is scalable and adaptable, providing an effective solution for solving DEs with multiple solutions and unknown parameters. Moreover, it has significant potential for various applications in scientific computing, such as modeling complex systems and solving inverse problems in physics, chemistry, biology, etc.

NSGA-PINN: A Multi-Objective Optimization Method for Physics-Informed Neural Network Training

This paper presents NSGA-PINN, a multi-objective optimization framework for effective training of Physics-Informed Neural Networks (PINNs). The proposed framework uses the Non-dominated Sorting Genetic Algorithm (NSGA-II) to enable traditional stochastic gradient optimization algorithms (e.g., ADAM) to escape local minima effectively. Additionally, the NSGA-II algorithm enables satisfying the initial and boundary conditions encoded into the loss function during physics-informed training precisely. We demonstrate the effectiveness of our framework by applying NSGA-PINN to several ordinary and partial differential equation problems. In particular, we show that the proposed framework can handle challenging inverse problems with noisy data.

On Approximating the Dynamic Response of Synchronous Generators via Operator Learning: A Step Towards Building Deep Operator-based Power Grid Simulators

This paper designs an Operator Learning framework to approximate the dynamic response of synchronous generators. One can use such a framework to (i) design a neural-based generator model that can interact with a numerical simulator of the rest of the power grid or (ii) shadow the generator's transient response. To this end, we design a data-driven Deep Operator Network~(DeepONet) that approximates the generators' infinite-dimensional solution operator. Then, we develop a DeepONet-based numerical scheme to simulate a given generator's dynamic response over a short/medium-term horizon. The proposed numerical scheme recursively employs the trained DeepONet to simulate the response for a given multi-dimensional input, which describes the interaction between the generator and the rest of the system. Furthermore, we develop a residual DeepONet numerical scheme that incorporates information from mathematical models of synchronous generators. We accompany this residual DeepONet scheme with an estimate for the prediction's cumulative error. We also design a data aggregation (DAgger) strategy that allows (i) employing supervised learning to train the proposed DeepONets and (ii) fine-tuning the DeepONet using aggregated training data that the DeepONet is likely to encounter during interactive simulations with other grid components. Finally, as a proof of concept, we demonstrate that the proposed DeepONet frameworks can effectively approximate the transient model of a synchronous generator.

Non-reversible Parallel Tempering for Deep Posterior Approximation

Parallel tempering (PT), also known as replica exchange, is the go-to workhorse for simulations of multi-modal distributions. The key to the success of PT is to adopt efficient swap schemes. The popular deterministic even-odd (DEO) scheme exploits the non-reversibility property and has successfully reduced the communication cost from $O(P^2)$ to $O(P)$ given sufficiently many $P$ chains. However, such an innovation largely disappears in big data due to the limited chains and few bias-corrected swaps. To handle this issue, we generalize the DEO scheme to promote non-reversibility and propose a few solutions to tackle the underlying bias caused by the geometric stopping time. Notably, in big data scenarios, we obtain an appealing communication cost $O(P\log P)$ based on the optimal window size. In addition, we also adopt stochastic gradient descent (SGD) with large and constant learning rates as exploration kernels. Such a user-friendly nature enables us to conduct approximation tasks for complex posteriors without much tuning costs.

DeepGraphONet: A Deep Graph Operator Network to Learn and Zero-shot Transfer the Dynamic Response of Networked Systems

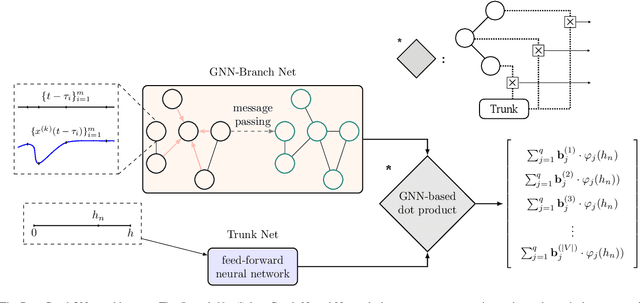
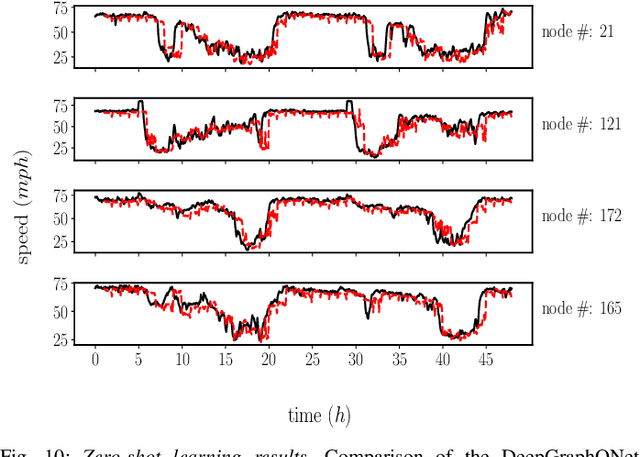
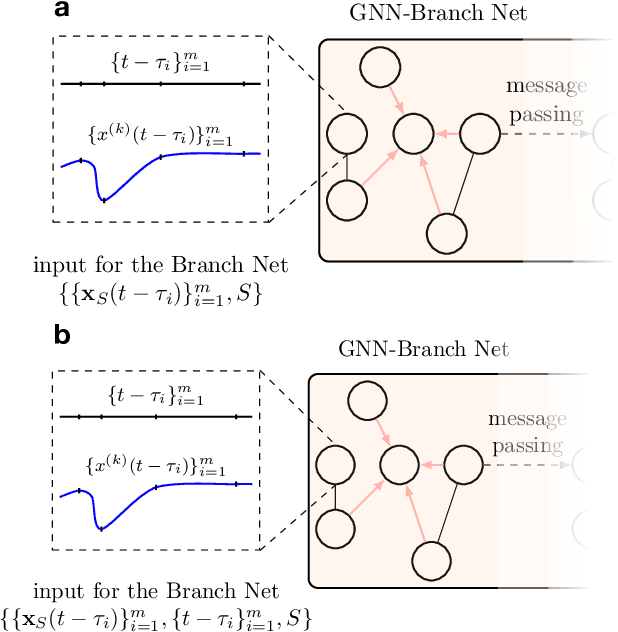
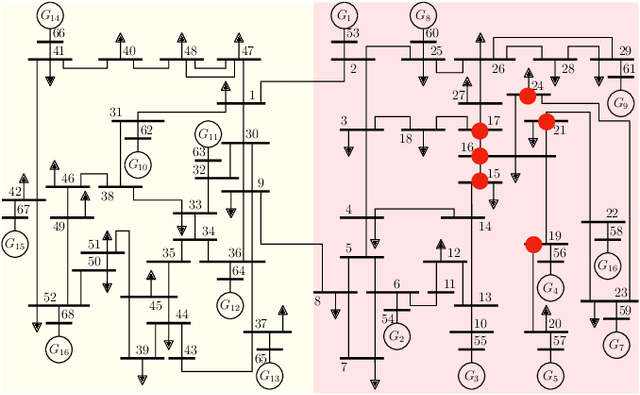
This paper develops a Deep Graph Operator Network (DeepGraphONet) framework that learns to approximate the dynamics of a complex system (e.g. the power grid or traffic) with an underlying sub-graph structure. We build our DeepGraphONet by fusing the ability of (i) Graph Neural Networks (GNN) to exploit spatially correlated graph information and (ii) Deep Operator Networks~(DeepONet) to approximate the solution operator of dynamical systems. The resulting DeepGraphONet can then predict the dynamics within a given short/medium-term time horizon by observing a finite history of the graph state information. Furthermore, we design our DeepGraphONet to be resolution-independent. That is, we do not require the finite history to be collected at the exact/same resolution. In addition, to disseminate the results from a trained DeepGraphONet, we design a zero-shot learning strategy that enables using it on a different sub-graph. Finally, empirical results on the (i) transient stability prediction problem of power grids and (ii) traffic flow forecasting problem of a vehicular system illustrate the effectiveness of the proposed DeepGraphONet.

AMS-Net: Adaptive Multiscale Sparse Neural Network with Interpretable Basis Expansion for Multiphase Flow Problems

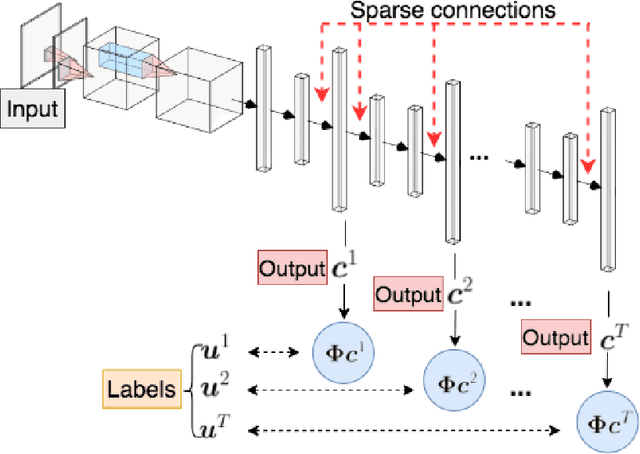
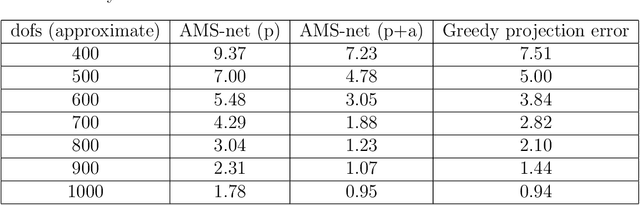
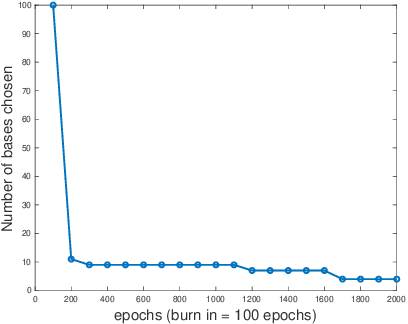
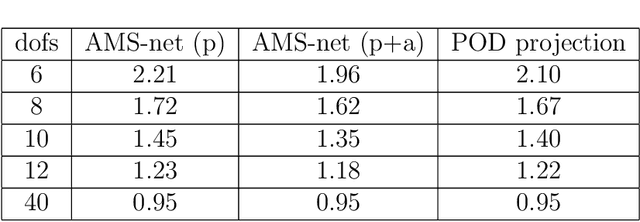
In this work, we propose an adaptive sparse learning algorithm that can be applied to learn the physical processes and obtain a sparse representation of the solution given a large snapshot space. Assume that there is a rich class of precomputed basis functions that can be used to approximate the quantity of interest. We then design a neural network architecture to learn the coefficients of solutions in the spaces which are spanned by these basis functions. The information of the basis functions are incorporated in the loss function, which minimizes the differences between the downscaled reduced order solutions and reference solutions at multiple time steps. The network contains multiple submodules and the solutions at different time steps can be learned simultaneously. We propose some strategies in the learning framework to identify important degrees of freedom. To find a sparse solution representation, a soft thresholding operator is applied to enforce the sparsity of the output coefficient vectors of the neural network. To avoid over-simplification and enrich the approximation space, some degrees of freedom can be added back to the system through a greedy algorithm. In both scenarios, that is, removing and adding degrees of freedom, the corresponding network connections are pruned or reactivated guided by the magnitude of the solution coefficients obtained from the network outputs. The proposed adaptive learning process is applied to some toy case examples to demonstrate that it can achieve a good basis selection and accurate approximation. More numerical tests are performed on two-phase multiscale flow problems to show the capability and interpretability of the proposed method on complicated applications.